Przyspieszenie to zmiana prędkości w czasie. W rzeczywistym scenariuszu przyspieszenie również zmienia się w czasie. Na przykład podróżujesz samochodem z jednego miasta do drugiego. Wtedy w tym przypadku przyspieszysz bardziej w przypadku pustej drogi i zmniejszysz prędkość w przypadku korka. Tę zmianę przyspieszenia można zaobserwować, wykreślając przyspieszenie w funkcji czasu na wykresie. Nazywa się to wykresem czasu przyspieszania. W tym artykule poznamy szczegółowo wykres czasu przyspieszania i na jego podstawie rozwiążemy problemy.

Java lokalna data i czas

Co to jest wykres czasu przyspieszania?

Wykres przyspieszenia w czasie służy do przedstawienia zależności pomiędzy przyśpieszenie oraz czas, gdzie przyspieszenie jest zmienną niezależną wykreśloną na osi Y, a czas jest zmienną zależną wykreśloną na osi X. Uzyskuje się go, gdy uzyskane dane dotyczące przyspieszenia i czasu nanosi się na prostokątny wykres podczas badania ruchu ciała. Za pomocą wykresu przyspieszenia-czasu możemy wyznaczyć zmianę prędkości w danym przedziale czasu. Wyznaczając pole pod krzywą wykresu przyspieszenia w czasie, możemy znaleźć zmianę prędkości obiektu w ruchu w pewnym okresie.

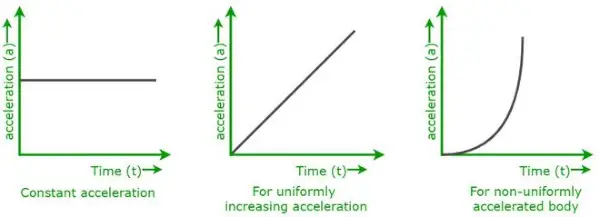
Wykresy pokazane powyżej to wykresy przyspieszenia w funkcji czasu dla różnych typów ruchu ciała.

1. Gdy ciało porusza się ze stałym przyspieszeniem,
2. Gdy ciało porusza się ruchem jednostajnym ze wzrostem przyspieszenia.
3. Gdy ciało porusza się nierównomiernie ze zmiennym przyspieszeniem.

Wnioski

Poniżej przedstawiono wnioski wyciągnięte z wykresów przyspieszenia w czasie.

• Nachylenie wykresu przyspieszenia w czasie wynosi △a/△t.
• Obszar pod wykresem przyspieszenia w funkcji czasu przedstawia zmianę prędkości.

Pozwalać,

△w będzie zmianą prędkości,

△a będzie zmianą przyspieszenia,

△t być zmianą w czasie.

Teraz, pole pod krzywą = △v

Wiemy, że przyspieszenie ciała nazywa się szybkością zmiany prędkości w danym okresie czasu.

Więc,

△a = △v/△t

Teraz, mnożąc przez △t po obu stronach, otrzymujemy,

△v = △a × △t (w to pole pod krzywą w czasie przyspieszania wykres )

• Dla obiektu poruszającego się ze stałym przyspieszeniem, tj. przyspieszenie jest takie samo w każdym przedziale czasu. Zatem nachylenie wykresu przyspieszenia w czasie wynosi zero, a wykres będzie równoległy do ​​osi czasu.

Przyspieszenie a opóźnienie

Przyśpieszenie: Przyspieszenie ciała określa się jako szybkość zmiany prędkości w danym okresie czasu. Jest to wielkość wektorowa mierzona w m/s².

Przyspieszenie = zmiana prędkości/czasu

tutaj zmiana prędkości jest dodatnia.

Załóżmy, że ciało poruszające się ze stałą prędkością zwiększa swoją prędkość. Tempo wzrostu prędkości nazywamy przyspieszeniem ciała. Niech u będzie prędkością początkową, v będzie prędkością końcową, a t będzie przedziałem czasu, wówczas przyspieszenie ciała wyraża się wzorem:

Przyspieszenie (a) = (v – u)/t

Przykład: Przykładem przyspieszenia w życiu codziennym jest skręcanie samochodem na zakręcie. Prędkość samochodu wzrasta wraz ze zmianą kierunku, co powoduje przyspieszenie. Przyspieszenie wzrasta wraz ze wzrostem prędkości skrętu.

Opóźnienie: Opóźnienie ciała określa się jako tempo zmiany prędkości w danym okresie czasu. Opóźnienie oznacza ujemne przyspieszenie.

Opóźnienie = zmiana prędkości/czasu

tutaj zmiana prędkości jest ujemna.

Załóżmy, że ciało poruszające się ze stałą prędkością zmniejsza swoją prędkość. Tempo zmniejszania się prędkości nazywa się opóźnieniem ciała. Niech u będzie prędkością początkową, v będzie prędkością końcową, a t będzie przedziałem czasu, wówczas opóźnienie ciała wyraża się wzorem:

Opóźnienie = (v – u)/t

Przykład: Prawdziwym przykładem opóźnienia jest wyłączenie wentylatora. Kiedy wyłącznik poruszającego się wentylatora jest wyłączony, prędkość obrotowa łopatek wentylatora stopniowo maleje. To tempo zmniejszania się prędkości wentylatora nazywa się opóźnieniem.

Sprawdź także to:

• Wykresy odległości i czasu
• Wykresy prędkości i czasu

Przykładowe problemy na wykresach czasu przyspieszania

Zadanie 1: Z poniższego wykresu przyspieszenia w funkcji czasu określ zmianę prędkości.

Rozwiązanie:

Aby znaleźć zmianę prędkości ciała, należy wyznaczyć pole pod krzywą.

Aby więc znaleźć zmianę prędkości obiektu, musimy obliczyć pole trójkąta.

△v = pole trójkąta

= ½ × 25 × 6

△v = 75 m/s.

Zatem zmiana prędkości wynosi 75 m/s.

Zadanie 2: Z poniższego wykresu przyspieszenia w funkcji czasu znajdź prędkość początkową ciała, jeśli jego prędkość końcowa wynosi 55 m/s.

Rozwiązanie:

Aby znaleźć zmianę prędkości ciała, należy wyznaczyć pole pod krzywą. Z wykresu możemy zauważyć, że ma on prostokąt i trójkąt. Aby więc znaleźć zmianę prędkości obiektu, musimy obliczyć pole tych figur.

△v = pole trójkąta + pole prostokąta

= ½ × 8 × 6 + 2 × 8

△v = 24 + 16 = 42 m/s

Wiemy to,

△v = prędkość końcowa – prędkość początkowa

42 = 55 – cale_I

W_I= 55 – 42 = 13 m/s

Zatem prędkość początkowa wynosi 13 m/s.

Zadanie 3: Z poniższego wykresu przyspieszenia w funkcji czasu określ prędkość w chwili t = 6 sekund, jeśli v(0) = 0.

Rozwiązanie:

Przyspieszenie jest dane przez;

a = dv/dt

⇒ dv = (a)dt

Całkując po obu stronach, otrzymujemy

∫dv = ∫(a) dt

⇒ v = ∫(1,5) dt

⇒ v(t) = 1,5t + c, gdzie c jest stałą

⇒ v(0) = 0

⇒ do = 0

Teraz v(t) = 1,5t

v(6) = 1,5 × 6 = 9 m/s

Zatem prędkość w chwili t = 6 s wynosi 9 m/s.

Problem 4: Co wskazuje obszar pod wykresem czasu przyspieszenia?

Rozwiązanie:

Obszar pod wykresem przyspieszenia w funkcji czasu przedstawia zmianę prędkości.

Niech △v będzie zmianą prędkości, △a będzie zmianą przyspieszenia, a △t będzie zmianą czasu.

Teraz pole pod krzywą = △v

Wiemy, że przyspieszenie ciała określa się jako stosunek zmiany prędkości w danym okresie czasu.

Więc,

△a = △v/△t

Teraz, mnożąc przez △t po obu stronach, otrzymujemy,

△v = △a × △t

Zatem pole pod krzywą uzyskuje się poprzez pomnożenie zmiany przyspieszenia i zmiany czasu.

Problem 5: Co oznacza szarpnięcie na wykresie czasu przyspieszania?

Rozwiązanie:

Szarpnięcie to nagła zmiana przyspieszenia poruszającego się ciała, a nachylenie wykresu a-t reprezentuje szarpnięcie.

Nachylenie wykresu przyspieszenia-czasu = szarpnięcie = △a/△t

Wykres czasu przyspieszania – często zadawane pytania

Co to jest wykres przyspieszenia w czasie?

Wykres przyspieszenia w czasie pokazuje, jak przyspieszenie zmienia się w czasie dla obiektu poruszającego się po linii prostej. Przedstawia wykres przyspieszenia na osi y w funkcji czasu na osi x.

Jak obliczyć pole pod wykresem zależności przyspieszenia od czasu i co ono reprezentuje?

Obszar pod wykresem przyspieszenia w czasie przedstawia zmianę prędkości w okresie objętym wykresem. Aby obliczyć tę powierzchnię, zazwyczaj sumuje się pola prostokątów lub trapezów mieszczących się pod krzywą, które odpowiadają różnym przedziałom czasu, podczas których przyspieszenie jest stałe.

Czy możesz określić prędkość obiektu w określonym czasie na podstawie wykresu przyspieszenia w czasie?

Bezpośrednie określenie prędkości chwilowej w określonym czasie na podstawie wykresu przyspieszenia w funkcji czasu nie jest możliwe. Można jednak obliczyć zmianę prędkości w danym okresie, znajdując obszar pod wykresem w tym okresie. Znajomość prędkości początkowej pozwala wyznaczyć prędkość końcową.

Co oznacza ujemne przyspieszenie na tego typu wykresie?

Ujemne przyspieszenie na wykresie przyspieszenia w funkcji czasu oznacza zwalnianie, podczas którego prędkość obiektu maleje, jeśli obiekt porusza się w kierunku dodatnim. Jeśli obiekt porusza się w kierunku uważanym za ujemny, wówczas ujemne przyspieszenie oznacza wzrost prędkości.

Jak znaleźć średnie przyspieszenie na podstawie wykresu przyspieszenia w funkcji czasu?

Średnie przyspieszenie można wyznaczyć, znajdując całkowitą zmianę prędkości (sumując obszary pod krzywą, uwzględniając kierunek) i dzieląc ją przez całkowity przedział czasu. Wizualnie można to przedstawić jako prostokąt, którego powierzchnia jest równa całkowitej powierzchni pod wykresem czasu przyspieszenia.

Co reprezentuje nachylenie wykresu przyspieszenia w funkcji czasu?

Nachylenie wykresu przyspieszenia w czasie wskazuje szybkość zmiany przyspieszenia w czasie, co jest znane jako szarpnięcie. Strome zbocze oznacza szybką zmianę przyspieszenia.

Jak przedstawić ciało w spoczynku na wykresie przyspieszenia w czasie?

Ciało pozostające w spoczynku lub poruszające się ze stałą prędkością jest przedstawione na wykresie zależności przyspieszenia od czasu za pomocą linii wzdłuż osi czasu przy zerowym przyspieszeniu.

Jak interpretować wykres przyspieszenia w czasie?

Nachylenie wykresu przyspieszenia w funkcji czasu przedstawia szybkość zmiany przyspieszenia, gdzie bardziej strome nachylenie oznacza większą szybkość zmian.

Co reprezentuje obszar pod wykresem zależności przyspieszenia od czasu?

Obszar pod krzywą na wykresie przyspieszenia w czasie przedstawia zmianę prędkości obiektu. W szczególności reprezentuje prędkość końcową minus prędkość początkowa.