Prędkość to po prostu miara tego, jak szybko lub wolno porusza się obiekt, na przykład, jak szybko jedziesz samochodem. Tutaj mówimy o konkretnym rodzaju prędkości. Prędkość kątowa jest tylko rodzajem prędkości, ale w tym przypadku ciało musi poruszać się po torze kołowym.
Wzór na prędkość kątową
Prędkość kątową definiuje się jako szybkość zmiany przemieszczenia kątowego, czyli kąta, jaki wykonuje ciało po torze kołowym. Prędkość kątową oblicza się jako liczbę obrotów/obrotów wykonanych przez ciało w czasie. Prędkość kątowa jest oznaczona grecką literą „ω” znaną jako Omega. Jednostką prędkości kątowej w układzie SI jest rad/s.
Prędkość kątową oblicza się za pomocą dwóch różnych wzorów,
- ω = θ/t ω = v/r
Wyprowadzenie formuły
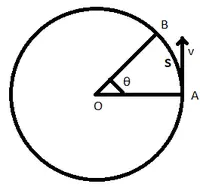
Rozważmy ciało poruszające się po torze kołowym o promieniu r pokazanym powyżej z prędkością liniową v. Załóżmy, że ciało porusza się z punktu A do B, pokonując drogę s po łuku kołowym i pokonując kąt θ w okresie t.
Ścieżka okrężna pokryta ciałem
Jak wiadomo, prędkość kątowa to szybkość zmiany przemieszczenia – prędkość kątowa, ω = θ/t
Zatem wzór na prędkość kątową wygląda następująco: ω = θ/t .
Inny wzór na prędkość kątową
Pomimo powyższego wzoru istnieje inny, szerzej stosowany wzór na obliczenie prędkości kątowej z punktu widzenia egzaminów konkursowych.
Ponieważ ω = θ/t ⇢ (1)
Teraz wiemy, że odległość przebyta przez łuk koła jest równa promieniowi razy przebyty kąt. Więc,
s = rθ
=> θ = s/r ⇢ (2)
usuń pamięć podręczną npmZ (1) i (2),
ω = s/(rt) ⇢ (3)
Również z ogólnego zrozumienia prędkości liniowych,
v = s/t ⇢ (4)
Z (3) i (4),
ω = v/r
Przykładowe problemy
Pytanie 1: Rozważmy ciało poruszające się po okręgu o promieniu 5 m. Obejmuje połowę obrotu w ciągu 5 sekund. Oblicz jego prędkość kątową.
Rozwiązanie:
W połowie obrotu kąt, jaki przebył, wynosi 180 stopni. W radianach jest równy π radianom.
ω = θ/t
=> ω = π/5 = 0,628 rad/s
Pytanie 2: Koło samochodu o promieniu 2m obraca się z prędkością liniową 10m/s. Oblicz jego prędkość kątową.
Rozwiązanie:
ω = v/r
ω = 10/2
= 5 rad/s
Pytanie 3: Rozważmy samochód wyścigowy poruszający się po torze kołowym z prędkością 18 km/h, a promień toru wynosi 0,2 m. Oblicz prędkość kątową samochodu.
Rozwiązanie:
v = 18 km/h = 5 m/s
r = 0,2 m
ω = v/r
= 5/0,2
= 25 rad/s
Pytanie 4: Samochód porusza się po okręgu o promieniu 2 m z prędkością kątową 2 rad/s. Oblicz kąt w stopniach, o jaki samochód przejedzie w ciągu 2 s.
Rozwiązanie:
Dany, ω = 2 rad/s i t = 2s
Ponieważ ω = θ/t => θ = ωt
=> θ = (2 × 2) = 4 rad
W stopniach θ = 4 × (180/π) = 229,18 stopnia
Pytanie 5: Ile obrotów wykonało ciało poruszające się po torze kołowym z prędkością kątową 7π rad/s w ciągu 0,5 s?
Rozwiązanie:
Przy założeniu ω = 7π rad/s i t = 0,5s
Ponieważ ω = θ/t => θ = ωt
θ = (7π × 0,5) = 3,5π
W 2π rad pokrycie obrotów wynosi 1
=> W 1 rad pokonany obrót wynosi (1/2π)
=> W 3,5π rad, obroty = 3,5π/2π = 1,75 obrotu
Zatem ciało wykona 1 pełny obrót i 3/4 następnego obrotu w czasie 0,5 s.
Pytanie 6: Jaka będzie prędkość kątowa ciała poruszającego się po okręgu o promieniu 2 m, który pokrywa 4 m łuku o długości 5 s.
Rozwiązanie:
Biorąc pod uwagę s = 4 m, r = 2 m, t = 5 s
Korzystając ze wzoru s = rθ => θ = s/r
θ = 4/2 = 2 rad
Ponieważ ω = θ/t
ustawienie ścieżki Pythona=> ω = 2/5 = 0,4 rad/s