System liczb binarnych to system liczbowy używany do reprezentowania różnych liczb za pomocą tylko dwóch symboli 0 i 1. Słowo binarny pochodzi od słowa bi, które oznacza dwa. Dlatego ten system liczbowy nazywa się systemem liczb binarnych. Zatem system liczb binarnych to system, który ma tylko dwa symbole.
Ogólnie rzecz biorąc, istnieją różne typy systemów liczbowych, a wśród nich cztery główne to:
- Binarny system liczbowy (system liczbowy z podstawą 2)
- System liczb ósemkowych (system liczbowy z podstawą 8)
- System liczb dziesiętnych (system liczbowy z podstawą 10)
- Szesnastkowy system liczbowy (system liczbowy z podstawą 16)
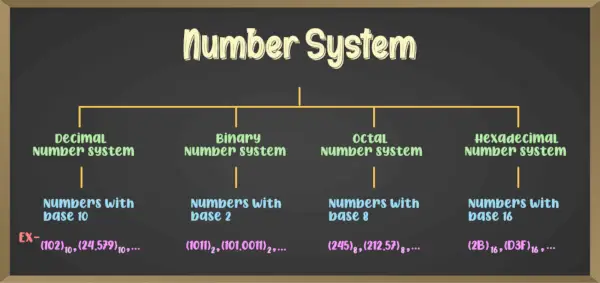
Tutaj dowiemy się tylko o systemie liczb binarnych. Ten system liczbowy jest bardzo przydatny do wyjaśniania zadań komputerowi. W systemie liczb binarnych mamy dwa stany 0 i 1 i te dwa stany są reprezentowane przez dwa stany tranzystora. Jeśli prąd przepływa przez tranzystor, komputer odczytuje wartość 1, a jeśli w tranzystorze nie ma prądu, odczytuje wartość 0. Zatem, zmieniając prąd, komputer odczytuje system liczb binarnych. Każda cyfra w systemie binarnym nazywana jest bitem.
W tym artykule dowiemy się szczegółowo o systemie liczb binarnych, konwersji systemu liczb binarnych, tabeli binarnej, działaniu liczb binarnych, przykładach i innych szczegółach.
Spis treści
- System liczb binarnych
- Tabela liczb binarnych
- Konwersja binarna na dziesiętną
- Konwersja dziesiętna na binarną
- Operacje arytmetyczne na liczbach binarnych
- Uzupełnienie 1 i 2 liczby binarnej
- Zastosowania binarnego systemu liczbowego
- Przykład systemu liczb binarnych
System liczb binarnych
Binarny system liczbowy to system liczbowy, w którym używamy dwóch cyfr 0 i 1 do wykonywania wszystkich niezbędnych operacji. W systemie liczb binarnych podstawą jest liczba 2. Podstawa systemu liczb binarnych nazywana jest także podstawą liczby systemu liczbowego .
W systemie liczb binarnych liczbę reprezentujemy jako:
- (11001)2
W powyższym przykładzie podana jest liczba binarna, której podstawa wynosi 2. W systemie liczb binarnych każda cyfra nazywana jest bitem. W powyższym przykładzie jest 5 cyfr.
Tabela liczb binarnych
| Liczba dziesiętna | Liczba binarna | Liczba dziesiętna | Liczba binarna |
|---|---|---|---|
| 1 | 001 | jedenaście | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | piętnaście | 1111 |
| 6 | 110 | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 | 20 | 10100 |
Konwersja binarna na dziesiętną
Liczbę binarną przekształca się na liczbę dziesiętną, mnożąc każdą cyfrę liczby binarnej przez potęgę 1 lub 0 do odpowiedniej potęgi 2. Rozważmy, że liczba binarna ma n cyfr, B = an-1…A3A2A1A0. Teraz odpowiednia liczba dziesiętna jest podana jako
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Przeanalizujmy przykład, aby lepiej zrozumieć tę koncepcję.
Przykład: Konwertuj (10011) 2 do liczby dziesiętnej.
Rozwiązanie:
Podana liczba binarna to (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Stąd liczba binarna (10011)2wyraża się jako (19)10.
Konwersja dziesiętna na binarną
Liczbę dziesiętną przekształca się na liczbę binarną, dzieląc daną liczbę dziesiętną przez 2 w sposób ciągły, aż otrzymamy iloraz równy 1, a następnie zapisujemy liczby od dołu do góry.
Przeanalizujmy przykład, aby lepiej zrozumieć tę koncepcję.
Przykład: Konwertuj (28) 10 na liczbę binarną.
Rozwiązanie:
Stąd (28)10wyraża się jako (11100)2.
Operacje arytmetyczne na liczbach binarnych
Z łatwością możemy wykonywać różne operacje na liczbach binarnych. Różne operacje arytmetyczne na liczbie binarnej obejmują:
- Dodatek binarny
- Odejmowanie binarne
- Mnożenie binarne
- Podział binarny
Teraz dowiedzmy się o tym samym szczegółowo.
Dodatek binarny
Wynik dodania dwóch liczb binarnych jest również liczbą binarną. Aby otrzymać wynik dodania dwóch liczb binarnych, musimy dodać cyfrę liczb binarnych po cyfrze. Dodana poniżej tabela przedstawia zasadę dodawania binarnego.
| Liczba binarna (1) | Liczba binarna (2) | Dodatek | Nosić |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 czcionka gimp | 0 |
| 1 | 1 | 0 | 1 |
Odejmowanie binarne
Wynik odjęcia dwóch liczb binarnych jest również liczbą binarną. Aby otrzymać wynik odejmowania dwóch liczb binarnych, musimy odjąć cyfrę liczb binarnych po cyfrze. Dodana poniżej tabela przedstawia zasadę odejmowania binarnego.
| Liczba binarna (1) | Liczba binarna (2) | Odejmowanie | Pożyczyć |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Mnożenie binarne
Proces mnożenia liczb binarnych jest podobny do mnożenia liczb dziesiętnych. Zasady mnożenia dowolnych dwóch liczb binarnych podano w tabeli,
| Liczba binarna (1) | Liczba binarna (2) | Mnożenie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Podział binarny
The metoda dzielenia dla liczb binarnych jest podobna do metody dzielenia liczb dziesiętnych. Przeanalizujmy przykład, aby lepiej zrozumieć tę koncepcję.
Przykład: Podziel (101101) 2 przez (110) 2
Rozwiązanie:
Uzupełnienie 1 i 2 liczby binarnej
- Dopełnienie liczby binarnej 1 uzyskuje się poprzez odwrócenie cyfr liczby binarnej.
Przykład: Znajdź uzupełnienie do 1 (10011) 2 .
Rozwiązanie:
Podana liczba binarna to (10011)2
Teraz, aby znaleźć uzupełnienie do jedynki, musimy odwrócić cyfry danej liczby.
Zatem uzupełnienie 1 do (10011)2jest (01100)2
- Dopełnienie liczby binarnej 2 uzyskuje się poprzez odwrócenie cyfr liczby binarnej, a następnie dodanie 1 do najmniej znaczącego bitu.
Przykład: Znajdź uzupełnienie do 2 (1011) 2 .
Rozwiązanie:
Podana liczba binarna to (1011)2
Aby znaleźć uzupełnienie do 2, najpierw znajdź uzupełnienie do 1, tj. (0100)2
Teraz, dodając 1 do najmniej znaczącego bitu, otrzymamy (0101)2
Stąd uzupełnienie do 2 (1011)2jest (0101)2
Zastosowania binarnego systemu liczbowego
Systemy liczb binarnych są wykorzystywane do różnych celów, a najważniejszym zastosowaniem systemu liczb binarnych jest:
jak pobrać wideo z YouTube VLC
- System liczb binarnych jest używany we wszystkich urządzeniach cyfrowych do wykonywania różnych operacji.
- Języki programowania wykorzystują system liczb binarnych do kodowania i dekodowania danych.
- System liczb binarnych jest używany w naukach o danych do różnych celów itp.
Czytaj więcej,
- Formuła binarna
- Różnica między dziesiętnym i binarnym systemem liczbowym
Przykład systemu liczb binarnych
Przykład 1: Konwersja liczby dziesiętnej (98) 10 do wersji binarnej.
Rozwiązanie:
Zatem liczba binarna dla (98)10jest równe (1100010)2
Przykład 2: Konwersja liczby binarnej (1010101) 2 na liczbę dziesiętną.
Rozwiązanie:
Podana liczba binarna (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1×26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Zatem liczba binarna (1010101)2jest równe (85)10w systemie dziesiętnym.
Przykład 3: Podziel (11110) 2 przez (101) 2
Rozwiązanie:
Przykład 4: Dodaj (11011) 2 i (10100) 2
Rozwiązanie:
Stąd (11011)2+ (10100)2= (101111)2
Przykład 5: Odejmij (11010) 2 i (10110) 2
Rozwiązanie:
Stąd (11010)2– (10110)2= (00100)2
Przykład 6: Pomnóż (1110) 2 i (1001) 2 .
Rozwiązanie:
Zatem (1110)2× (1001)2= (1111110)2
Często zadawane pytania dotyczące systemu liczb binarnych
Co to jest system liczb binarnych?
Binarny system liczbowy to jeden z czterech systemów liczbowych używanych do przedstawiania liczb za pomocą tylko dwóch cyfr, 0 i 1. W systemie liczb binarnych cyfry nazywane są „bitami”. System liczb binarnych jest używany przez komputery do wykonywania różnych obliczeń.
Co to jest B To?
Bit w systemie liczb binarnych definiuje się jako pojedynczą cyfrę, która przechowuje wartość „0” lub „1”.
Co to jest Nibble?
Grupa czterech cyfr nazywa się Niblle.
Jaka jest wartość binarna liczby 10?
Wartość binarna liczby 10 to (1010)2
Jakie są rodzaje systemów liczbowych?
Istnieją różne typy systemów liczbowych, a niektóre z nich to:
- System liczb binarnych
- System liczb ósemkowych
- Dziesiętny system liczbowy
- Szesnastkowy system liczbowy
Jak obliczyć liczby binarne?
Liczby binarne oblicza się na podstawie liczb dziesiętnych, dzieląc liczbę dziesiętną przez 2 i zapisując resztę. Następnie układamy wszystkie reszty od najnowszego do najstarszego, aby otrzymać liczbę binarną.
Jak dodać liczby binarne?
Liczby binarne dodaje się za pomocą wzorów zapisanych poniżej,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (przenieść 1)






