- Bitowy operator XOR jest również znany jako Ekskluzywne LUB
- Oznacza się to za pomocą „^”
- Jak sama nazwa wskazuje, działa na poziom bitowy operandów.
- Bitowy operator XOR należy do kategorii operatorów bitowych.
- W bitowym wyłącznym operatorze OR (XOR) wymagane są dwa operandy, które są oddzielone symbolem XOR, tj. „^”.
- Aby określić wynik lub wynik, który pojawi się po zastosowaniu operatora XOR na dwóch operandach, musimy postępować zgodnie z tabelą prawdy logicznej operatora XOR.
- Tabela prawdy XOR to tablica matematyczna zbudowana przy użyciu właściwej logiki operatora XOR.
- Logika zastosowana za operatorem XOR jest następująca: za każdym razem, gdy na obu przypadkach zostanie zastosowana operacja XOR różny bitów dwóch operandów, wówczas wynik będzie zawsze generowany „1”, i jeśli operacja XOR zostanie zastosowana na obu To samo bitów dwóch operandów, wówczas wynik generuje wynik „0”.
Tabela prawdy wyłącznego operatora OR (XOR).
Niech będą dwa operandy; pierwszy to A, a drugi to B, całkowita kombinacja danych wejściowych utworzonych przez te dwa operandy wyniesie 4. Korzystając z poniższej tabeli prawdy XOR, określimy odpowiedni wynik. Wynik zostanie zapisany w języku C tutaj C = ZA ^ B.
W tej tabeli prawdy dane wejściowe pobieramy w postaci bitów, tj. 0 i 1, a dane wyjściowe będą również generowane w postaci bitów, tj. 0 i 1.
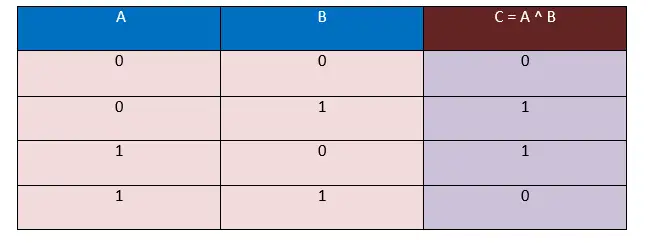
Tutaj, w powyższej tabeli XOR Truth, obserwujemy, że gdy wartości argumentów A i B są różne, tj. ( 0, 1 ), ( 1, 0 ), wynik zawsze będzie wynosić 1. A kiedy wartości argumentów A i B są takie same, tj. ( 0, 0 ), ( 1, 1 ), wynik zawsze będzie wynosić 0.
Podobnie w ten sposób możemy narysować tablicę prawdy dla Wartość logiczna wartości -
Niech będą dwa operandy; pierwszy jest A i drugie jest B . Całkowita liczba kombinacji danych wejściowych utworzonych przez te dwa operandy wyniesie 4. Korzystając z poniższej tabeli prawdy XOR, określimy odpowiednie dane wyjściowe. Wynik zostanie zapisany w C, tutaj C = A ^ B.
W tej tabeli prawdy dane wejściowe przyjmujemy w postaci wartości prawdy, tj. prawdy ( T ) i fałszu ( F ). Dane wyjściowe będą również generowane w postaci wartości True, tj. T i F.

Tutaj, w powyższej tabeli XOR Truth, obserwujemy, że gdy wartości argumentów A i B są różne, tj. ( F, T ), ( T, F ), wynikiem zawsze będzie T. A kiedy wartości argumentów A i B są takie same, tj. ( F, F ), ( T, T ), wynikiem zawsze będzie F.
Z powyższych tabel wynika, że T (Prawda) jest oznaczona przez jeden, a F (Fałsz) jest oznaczona przez 0.
Kroki, aby rozwiązać dowolny problem -
- Operandy podane w zadaniu będą zawsze miały wartość dziesiętną.
- Najpierw musimy przekonwertować wartości operandów na dwójkowy
- Po przekształceniu wartości operandów na liczby binarne należy umieścić oba operandy jeden nad drugim.
- Pamiętaj, że zanim zastosujesz na nich wyłączną operację OR (XOR), sprawdź ilość cyfr w nich.
- Jeśli liczba cyfr nie jest zgodna, dodatkowe zera na lewym końcu małego operandu równoważą liczbę cyfr.
- Na koniec, korzystając z powyższej tabeli prawdy, zastosuj operację XOR na operandach jeden po drugim, stosując operację XOR po jednym bicie na raz.
- Na koniec wynik jest generowany w postaci danych wyjściowych.
- Wynik będzie miał postać binarną. Teraz przekonwertuj postać binarną na postać dziesiętną i zanotuj wartość wyniku.
Wykonanie operacji Bitwise Exclusive OR (XOR) w C++
Przyjrzyjmy się bardziej szczegółowo wykonaniu operacji XOR w C++ za pomocą przykładów -
Przykład 1: Znajdź wyłączny OR wartości całkowitych; 10 i 14. Wyjaśnij to także i napisz kod wykonania w C++.
Rozwiązanie: Rozważmy dwie zmienne „a” i „b” do przechowywania odpowiednich dwóch argumentów podanych w powyższym pytaniu, tj. 10 i 14.
Tutaj a = 10 i b = 14.
Wykonamy poniższe kroki, aby znaleźć wyłączne OR danych dwóch operandów.
kolory Javy
- Wiemy, że 10 i 14 są w postaci dziesiętnej i aby zastosować bitową operację XOR, konieczne jest przekonwertowanie ich na postać binarną.
- Forma binarna „a”, tj. 10 to „1010” oraz Binarna forma „b”, tj. 14 to „1110”.
- Tutaj zauważamy, że liczba cyfr binarnych występujących w a wynosi cztery, a liczba cyfr binarnych występujących w b również wynosi 4; stąd liczba cyfr binarnych obecnych w obu zmiennych jest taka sama i już zbilansowana, nie musimy dodawać większej liczby zer, aby to zrównoważyć.
- Teraz sprowadź cyfry binarne obecne w „b” do cyfr binarnych występujących w „a”.
- Na koniec, stosując operację XOR jeden po drugim na odpowiednich bitach, dopasowuj i zanotuj wynik.
- Wygenerowany wynik będzie ostatecznie w formie binarnej, tak jak powyższe pytanie podano w postaci dziesiętnej, dlatego musimy przekonwertować wynik na postać dziesiętną.
Wyjaśnienie:
a = 10 (w formie dziesiętnej)
b = 14 (w formie dziesiętnej)
jak zmienić ciąg na int
Teraz dla XOR b musimy przekonwertować aib na postać binarną -
a = 1010 (w formie binarnej)
b = 1110 (w formie binarnej)
Teraz, stosując operację XOR na aib -
a = 1010
b = 1110
---------------
a ^ b = 0100 (W formie binarnej)
Wynikiem a ^ b jest 0100, który jest w postaci binarnej.
Teraz konwertujemy wynik do postaci dziesiętnej, czyli 4.
10^14 = 4
UWAGA: Korzystając z powyższej tabeli prawdy XOR, generowane są dane wyjściowe odpowiednich bitów.
Zastosujemy teraz bitową operację XOR na liczbach 10 i 14 w języku C++ i otrzymamy wynik, czyli 4.
Kod C++ dla powyższego przykładu:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Wyjście

Przykład 2: Znajdź wyłączny OR wartości całkowitych; 3 i 15. Wyjaśnij to także i napisz kod wykonania w C++.
Rozwiązanie: Rozważmy dwie zmienne „a” i „b” do przechowywania odpowiednich dwóch operandów podanych w powyższym pytaniu, tj. 3 i 15.
Tutaj a = 3 i b = 15.
silnia Java
Wykonamy poniższe kroki, aby znaleźć wyłączne OR danych dwóch operandów.
- Wiemy, że liczby 3 i 15 są w postaci dziesiętnej i aby zastosować bitową operację XOR, należy je przekonwertować do postaci binarnej.
- Forma binarna „a”, tj. 3 to 'jedenaście' oraz Binarna forma „b”, tj. 15 to „1111”.
- Tutaj zaobserwujemy, że liczba cyfr binarnych występujących w a wynosi dwa, a liczba cyfr binarnych występujących w b wynosi cztery; stąd liczba cyfr binarnych występujących w obu zmiennych nie jest taka sama. Zatem w przypadku niezrównoważenia musimy dodać więcej zer po lewej stronie dolnej liczby binarnej, tj. a, czyli „ jedenaście' , żeby to zrównoważyć.
- Po zbilansowaniu wartość a wynosi „0011” i b jest „1111”.
- Teraz sprowadź cyfry binarne obecne w „b” do cyfr binarnych występujących w „a”.
- Na koniec, stosując operację XOR jeden po drugim na odpowiednich bitach, dopasowuj i zanotuj wynik.
- Wygenerowany wynik będzie ostatecznie w formie binarnej, tak jak powyższe pytanie podano w postaci dziesiętnej, dlatego musimy przekonwertować wynik na postać dziesiętną.
Wyjaśnienie:
a = 3 (w formie dziesiętnej)
b = 15 (w formie dziesiętnej)
Teraz dla XOR b musimy przekonwertować aib na postać binarną -
a = 0011 (w formie binarnej)
b = 1111 (w formie binarnej)
Teraz, stosując operację XOR na aib -
polecenie arp-a
a = 0011
b = 1111
---------------
a ^ b = 1100 (W formie binarnej)
Wynikiem a ^ b jest 1100, co jest w postaci binarnej.
Teraz konwertujemy wynik do postaci dziesiętnej, czyli 12.
3^15 = 12
UWAGA: Korzystając z powyższej tabeli prawdy XOR, generowane są dane wyjściowe odpowiednich bitów.
Zastosujemy teraz bitową operację XOR na liczbach 3 i 15 w języku C++ i otrzymamy wynik, czyli 12.
Kod C++ dla powyższego przykładu:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Wyjście

