Znamy A drzewo jest nieliniową strukturą danych. Nie ma ograniczeń co do liczby dzieci. ACo to jest kompletne drzewo binarne?
Kompletne drzewo binarne to specjalny typ drzewa binarnego, w którym wszystkie poziomy drzewa są całkowicie wypełnione, z wyjątkiem węzłów najniższego poziomu, które są wypełniane od lewej strony.

Kompletne drzewo binarne
Niektóre terminy związane z pełnym drzewem binarnym:
- Źródło – Węzeł, w którym żadna krawędź nie pochodzi od rodzica. Przykład -węzeł A
- Dziecko – Węzeł posiadający pewne krawędzie przychodzące nazywany jest dzieckiem. Przykład – węzły B, F są dziećmi odpowiednio A i C.
- Rodzeństwo – Węzły mające tego samego rodzica są rodzeństwem. Przykład - D, E są rodzeństwem, ponieważ mają tego samego rodzica B.
- Stopień węzła – Liczba dzieci danego rodzica. Przykład – stopień A wynosi 2, a stopień C wynosi 1. Stopień D wynosi 0.
- Węzły wewnętrzne/zewnętrzne – Węzły liściowe są węzłami zewnętrznymi, a węzły inne niż liście są węzłami wewnętrznymi.
- Poziom – Policz węzły na ścieżce prowadzącej do węzła docelowego. Przykład — Poziom węzła D wynosi 2, ponieważ węzły A i B tworzą ścieżkę.
- Wysokość – Liczba krawędzi prowadzących do węzła docelowego. Korzeń znajduje się na wysokości 0. Przykład – Wysokość węzła E wynosi 2, ponieważ ma on dwie krawędzie od korzenia.
Właściwości kompletnego drzewa binarnego:
- Pełne drzewo binarne nazywa się właściwym drzewem binarnym, w którym wszystkie liście mają tę samą głębokość.
- W pełnym drzewie binarnym liczba węzłów na głębokości D Jest 2 D .
- W kompletnym drzewie binarnym z N wysokość węzłów drzewa wynosi log(n+1) .
- Wszystkie poziomy z wyjątkiem ostatniego poziomu są całkowicie pełne.
Idealne drzewo binarne vs Pełne drzewo binarne:
Drzewo binarne o wysokości „h” posiadające maksymalną liczbę węzłów to a doskonały drzewo binarne.
Dla danej wysokości H , maksymalna liczba węzłów wynosi 2 h+1 -1 .
A kompletny drzewo binarne o wysokości h jest doskonałym drzewem binarnym do wysokości h-1 , a na ostatnim poziomie elementy są przechowywane w kolejności od lewej do prawej.
Przykład 1:
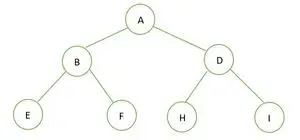
Drzewo binarne
Wysokość danego drzewa binarnego wynosi 2, a maksymalna liczba węzłów w tym drzewie wynosi n= 2h+1-1 = 22+1-1 = 23-1 = 7 .
Dlatego możemy stwierdzić, że tak idealne drzewo binarne .
Teraz, jeśli chodzi o kompletne drzewo binarne, jest ono pełne do wysokości h-1 tj.; 1, a elementy ostatniego poziomu są przechowywane w kolejności od lewej do prawej. Dlatego jest to również kompletne drzewo binarne. Oto reprezentacja elementów przechowywanych w tablicy

Element przechowywany w tablicy poziom po poziomie
W tablicy wszystkie elementy są przechowywane w sposób ciągły.
Przykład 2:
podstawowe pytania do rozmowy kwalifikacyjnej w języku Java
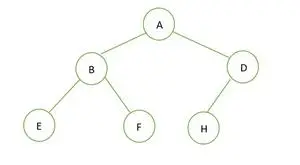
Drzewo binarne
Wysokość danego drzewa binarnego wynosi 2, a maksymalna liczba węzłów, jakie powinny się w nim znajdować, wynosi 2h+1– 1 = 22+1– 1 = 23– 1 = 7 .
Ale liczba węzłów w drzewie jest 6 . Dlatego tak jest nie jest idealnym drzewem binarnym .
Teraz, jeśli chodzi o kompletne drzewo binarne, jest ono pełne do wysokości h-1 tj.; 1 , a element ostatniego poziomu są przechowywane w kolejności od lewej do prawej. Dlatego jest to kompletne drzewo binarne . Zapisz element w tablicy i będzie tak;
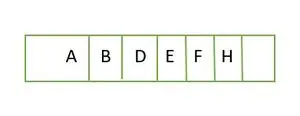
Element przechowywany w tablicy poziom po poziomie
Przykład 3:
np.gdzie
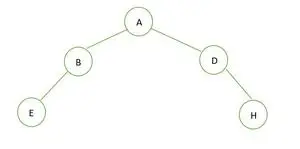
Drzewo binarne
Wysokość drzewa binarnego wynosi 2, a maksymalna liczba węzłów, jakie mogą w nim być, wynosi 7, ale jest tylko 5 węzłów, dlatego jest to nie jest idealnym drzewem binarnym .
W przypadku pełnego drzewa binarnego widzimy, że na ostatnim poziomie elementy nie są wypełniane w kolejności od lewej do prawej. Tak jest nie jest kompletnym drzewem binarnym .
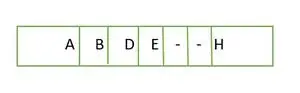
Element przechowywany w tablicy poziom po poziomie
Elementy tablicy nie są ciągłe.
Pełne drzewo binarne vs pełne drzewo binarne:
W przypadku pełnego drzewa binarnego każdy węzeł ma 2 dzieci lub 0 dzieci.
Przykład 1:
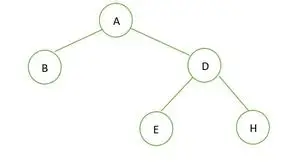
Drzewo binarne
W danym drzewie binarnym nie ma węzła o stopniu 1, ani 2, ani 0 dzieci na każdy węzeł, stąd jest to pełne drzewo binarne .
W przypadku pełnego drzewa binarnego elementy są przechowywane poziom po poziomie, a nie od lewej strony ostatniego poziomu. Dlatego tak jest nie jest kompletnym drzewem binarnym . Reprezentacja tablicowa to:
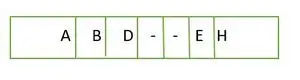
Element przechowywany w tablicy poziom po poziomie
Przykład 2:
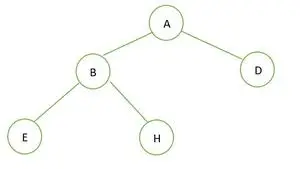
Drzewo binarne
W danym drzewie binarnym nie ma węzła o stopniu 1. Każdy węzeł ma stopień 2 lub 0. Jest to zatem pełne drzewo binarne .
W przypadku pełnego drzewa binarnego elementy są przechowywane poziom po poziomie i wypełniane od lewej strony ostatniego poziomu. Stąd to A kompletne drzewo binarne . Poniżej znajduje się tablicowa reprezentacja drzewa:
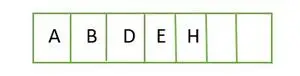
Element przechowywany w tablicy poziom po poziomie
Przykład 3:
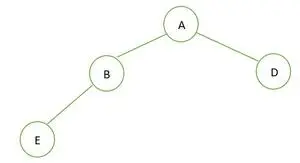
Drzewo binarne
W danym drzewie binarnym węzeł B ma stopień 1, co narusza właściwość pełnego drzewa binarnego i tak jest nie jest pełnym drzewem binarnym
wiek Mia Khalifa
W przypadku pełnego drzewa binarnego elementy są przechowywane poziom po poziomie i wypełniane od lewej strony ostatniego poziomu. Dlatego jest to kompletne drzewo binarne . Reprezentacja tablicowa drzewa binarnego to:
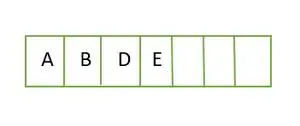
Element przechowywany w tablicy poziom po poziomie
Przykład 4:
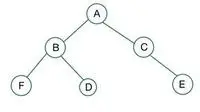
drzewo binarne
przekreślenie
W danym drzewie binarnym węzeł C ma stopień 1, co narusza właściwość pełnego drzewa binarnego i tak jest nie jest pełnym drzewem binarnym
W przypadku pełnego drzewa binarnego elementy są przechowywane poziom po poziomie i wypełniane od lewej strony ostatniego poziomu. Tutaj węzeł E narusza warunek. Dlatego tak jest nie jest kompletnym drzewem binarnym .
Tworzenie kompletnego drzewa binarnego:
Znamy A kompletne drzewo binarne to drzewo, w którym oprócz ostatniego poziomu (powiedzmy l )wszystkie pozostałe poziomy mają ( 2l ) węzły i węzły są ułożone od lewej do prawej strony.
Można to przedstawić za pomocą tablicy. Jeśli rodzicem jest to indeks I więc lewe dziecko jest w 2i+1 i właściwe dziecko jest w 2i+2 .
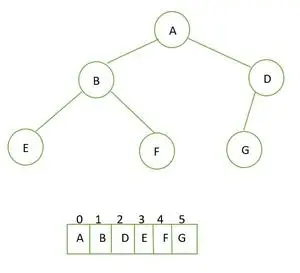
Kompletne drzewo binarne i jego reprezentacja tablicowa
Algorytm:
Za stworzenie A Kompletne drzewo binarne , potrzebujemy Krok 1: Zainicjuj korzeń nowym węzłem, gdy drzewo jest puste.
Krok 2: Jeśli drzewo nie jest puste, zdobądź przedni element
- Jeśli przedni element nie ma lewego dziecka, ustaw lewe dziecko na nowy węzeł
- Jeśli nie ma odpowiedniego dziecka, ustaw je jako nowy węzeł
Krok 3: Jeśli węzeł ma oboje dzieci, to Muzyka pop to z kolejki.
Krok 4: Kolejkuj nowe dane.
Ilustracja:
Rozważ poniższą tablicę:
Java analizuje ciąg znaków na int1. Pierwszy element będzie pierwiastkiem (wartość w indeksie = 0 )
A jest traktowane jako root
2. Następny element (w indeksie = 1 ) pozostanie i trzeci element (indeks = 2 ) będzie prawym dzieckiem root
B jako lewe dziecko i D jako prawe dziecko
3. czwarty (indeks = 3 ) i piąty element (indeks = 4 ) będzie lewym i prawym dzieckiem węzła B
E i F są lewym i prawym dzieckiem B
4. Następny element (indeks = 5 ) pozostanie dzieckiem węzła D
G staje się lewym dzieckiem węzła D
W ten sposób tworzone jest kompletne drzewo binarne.
Realizacja: Dla realizacji budowy kompletnego drzewa binarnego z poziomu kolejności przechodzenia podano w ten post .
Zastosowanie pełnego drzewa binarnego:
- Sortowanie sterty
- Struktura danych oparta na sortowaniu sterty
Sprawdź, czy dane drzewo binarne jest kompletne czy nie: Podążać ten post aby sprawdzić, czy dane drzewo binarne jest kompletne, czy nie.




