Funkcja usuwania służy do usunięcia określonego węzła z drzewa wyszukiwania binarnego. Musimy jednak usunąć węzeł z drzewa poszukiwań binarnych w taki sposób, aby nie naruszyć własności drzewa poszukiwań binarnych. Istnieją trzy sytuacje usunięcia węzła z drzewa wyszukiwania binarnego.
Węzeł do usunięcia jest węzłem liścia
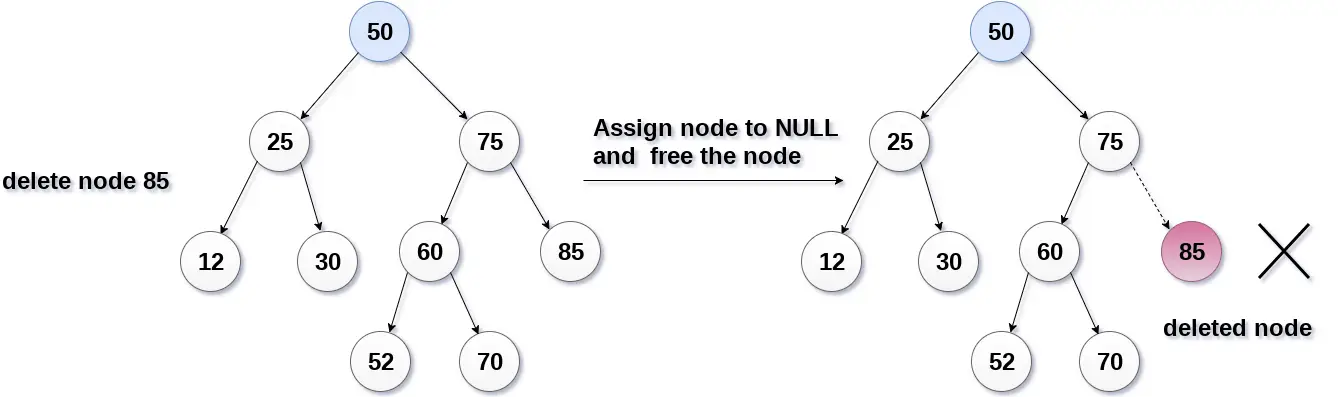
Jest to najprostszy przypadek, w tym przypadku zamień węzeł liścia na NULL i po prostu zwolnij przydzielone miejsce.
Na poniższym obrazku usuwamy węzeł 85, ponieważ węzeł jest węzłem liścia, dlatego węzeł zostanie zastąpiony wartością NULL, a przydzielone miejsce zostanie zwolnione.
Węzeł, który ma zostać usunięty, ma tylko jedno dziecko.
W takim przypadku zastąp węzeł jego potomkiem i usuń węzeł potomny, który teraz zawiera wartość, która ma zostać usunięta. Po prostu zastąp go wartością NULL i zwolnij przydzielone miejsce.
Na poniższym obrazku węzeł 12 ma zostać usunięty. Ma tylko jedno dziecko. Węzeł zostanie zastąpiony węzłem podrzędnym, a zastąpiony węzeł 12 (który jest teraz węzłem liścia) zostanie po prostu usunięty.

Węzeł, który ma zostać usunięty, ma dwoje dzieci.
Jest to nieco skomplikowana sprawa w porównaniu z dwoma pozostałymi sprawami. Jednakże węzeł, który ma zostać usunięty, jest zastępowany rekurencyjnie swoim porządnym następcą lub poprzednikiem, aż wartość węzła (do usunięcia) zostanie umieszczona na liściu drzewa. Po zakończeniu procedury zamień węzeł na NULL i zwolnij przydzielone miejsce.
Na poniższym obrazku należy usunąć węzeł 50, który jest węzłem głównym drzewa. Poniżej podano kolejność przechodzenia przez drzewo.
6, 25, 30, 50, 52, 60, 70, 75.
zamień 50 na jego następcę w kolejności 52. Teraz 50 zostanie przeniesione na liść drzewa, który zostanie po prostu usunięty.

Algorytm
Usuń (DRZEWO, ELEMENT)
Wpisz „nie znaleziono elementu w drzewie” W przeciwnym razie JEŚLI DANE PRZEDMIOTU
Usuń(DRZEWO->LEWO, ELEMENT)
W przeciwnym razie JEŚLI POZYCJA > DRZEWO -> DANE
Usuń(DRZEWO -> PRAWO, ELEMENT)
W przeciwnym razie JEŚLI DRZEWO -> W LEWO I DRZEWO -> W PRAWO
USTAW TEMP = findLargestNode (DRZEWO -> LEWO)
USTAW DRZEWO -> DANE = TEMP -> DANE
Usuń(DRZEWO -> LEWO, TEMP -> DANE)
W PRZECIWNYM RAZIE
TEMP USTAWIONA = DRZEWO
JEŻELI DRZEWO -> LEWO = NULL I DRZEWO -> PRAWO = NULL
USTAW DRZEWO = NULL
W przeciwnym razie JEŚLI DRZEWO -> LEWO != NULL
USTAW DRZEWO = DRZEWO -> W LEWO
W PRZECIWNYM RAZIE
USTAW DRZEWO = DRZEWO -> PRAWO
[KONIEC JEŚLI]
WOLNA TEMP
[KONIEC JEŚLI]
Funkcjonować:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 