Usuwanie węzła z drzewa AVL przebiega podobnie jak w przypadku drzewa wyszukiwania binarnego. Usunięcie może zakłócić współczynnik równowagi drzewa AVL i dlatego drzewo musi zostać ponownie zrównoważone, aby utrzymać AVL. W tym celu musimy wykonać rotacje. Dwa rodzaje rotacji to rotacja L i rotacja R. Tutaj omówimy rotacje R. Obroty L są ich lustrzanymi odbiciami.

Jeżeli węzeł przeznaczony do usunięcia znajduje się w lewym poddrzewie węzła krytycznego, to należy zastosować rotację L, w przeciwnym razie węzeł przeznaczony do usunięcia znajduje się w prawym poddrzewie węzła krytycznego , zastosowany zostanie obrót R.

Rozważmy, że A jest węzłem krytycznym, a B jest węzłem głównym lewego poddrzewa. Jeśli węzeł X, obecny w prawym poddrzewie A, ma zostać usunięty, mogą wystąpić trzy różne sytuacje:

Obrót R0 (Węzeł B ma współczynnik równowagi 0)

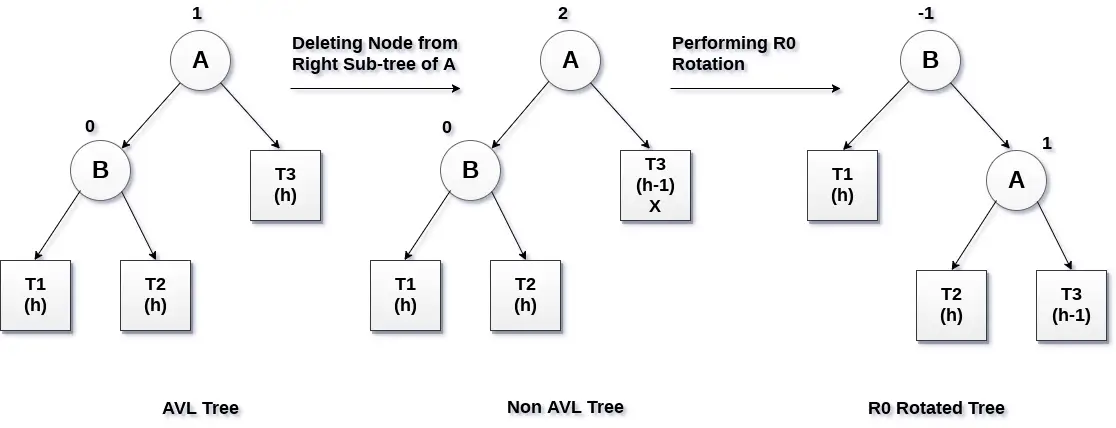
Jeżeli węzeł B ma współczynnik równowagi 0, a współczynnik równowagi węzła A zostanie zakłócony po usunięciu węzła X, wówczas drzewo zostanie zrównoważone poprzez obrócenie drzewa za pomocą rotacji R0.

Węzeł krytyczny A zostaje przesunięty na prawą stronę, a węzeł B staje się korzeniem drzewa, a T1 jest jego lewym poddrzewem. Poddrzewa T2 i T3 stają się lewym i prawym poddrzewem węzła A. Proces związany z rotacją R0 pokazano na poniższym obrazku.

Przykład:

Usuń węzeł 30 z drzewa AVL pokazanego na poniższym obrazku.

Rozwiązanie

W tym przypadku węzeł B ma współczynnik równowagi 0, dlatego drzewo zostanie obrócone przy użyciu obrotu R0, jak pokazano na poniższym obrazku. Węzeł B(10) staje się korzeniem, natomiast węzeł A zostaje przesunięty w jego prawą stronę. Prawe dziecko węzła B stanie się teraz lewym dzieckiem węzła A.

1 z 1000

Obrót R1 (Węzeł B ma współczynnik równowagi 1)

Obrót R1 należy wykonać, jeśli współczynnik równowagi Węzła B wynosi 1. Podczas obrotu R1 węzeł krytyczny A zostaje przesunięty w prawo, mając poddrzewa T2 i T3 jako odpowiednio lewe i prawe dziecko. T1 należy umieścić jako lewe poddrzewo węzła B.

Proces związany z rotacją R1 pokazano na poniższym obrazku.

Przykład

Usuń węzeł 55 z drzewa AVL pokazanego na poniższym obrazku.

Rozwiązanie :

Usunięcie 55 z drzewa AVL zakłóca współczynnik równowagi węzła 50, czyli węzła A, który staje się węzłem krytycznym. Jest to warunek obrotu R1, w którym węzeł A zostanie przesunięty w prawo (pokazany na obrazku poniżej). Prawa strona B staje się teraz lewą stroną A (tj. 45).

Proces związany z rozwiązaniem pokazano na poniższym obrazku.

Obrót R-1 (Węzeł B ma współczynnik równowagi -1)

Rotację R-1 należy wykonać, jeżeli węzeł B ma współczynnik równowagi -1. Przypadek ten traktowany jest w taki sam sposób jak obrót LR. W tym przypadku węzeł C, będący prawym dzieckiem węzła B, staje się węzłem głównym drzewa, a B i A są odpowiednio jego lewymi i prawymi dziećmi.

Poddrzewa T1, T2 stają się lewym i prawym poddrzewem B, podczas gdy T3, T4 stają się lewym i prawym poddrzewem A.

numerować alfabet

Proces związany z rotacją R-1 pokazano na poniższym obrazku.

Przykład

Usuń węzeł 60 z drzewa AVL pokazanego na poniższym obrazku.

Rozwiązanie:

w tym przypadku węzeł B ma współczynnik równowagi -1. Usunięcie węzła 60 zaburza współczynnik równowagi węzła 50, dlatego należy go obrócić R-1. Węzeł C, tj. 45, staje się korzeniem drzewa, a węzły B(40) i A(50) są jego lewym i prawym dzieckiem.