Algorytm wektora odległości jest iteracyjny, asynchroniczny i rozproszony.
Rozpowszechniane:Polega ona na tym, że każdy węzeł otrzymuje informacje od jednego lub większej liczby bezpośrednio podłączonych sąsiadów, wykonuje obliczenia, a następnie przesyła wynik z powrotem do swoich sąsiadów.Wielokrotny:Jest iteracyjny w tym sensie, że jego proces trwa do momentu, gdy nie będzie już dostępnych informacji do wymiany między sąsiadami.Asynchroniczny:Nie wymaga, aby wszystkie jego węzły współpracowały ze sobą w kroku blokowania.
• Algorytm wektora odległości jest algorytmem dynamicznym.
• Stosowany jest głównie w sieciach ARPANET i RIP.
• Każdy router utrzymuje tabelę odległości zwaną Wektor .

Trzy klucze do zrozumienia działania algorytmu routingu wektora odległości:

Wiedza o całej sieci:Każdy router dzieli się swoją wiedzą w całej sieci. Router wysyła zebraną wiedzę o sieci do swoich sąsiadów.Routing tylko do sąsiadów:Router wysyła swoją wiedzę o sieci tylko do tych routerów, które mają bezpośrednie łącza. Router wysyła przez porty wszystko, co ma na temat sieci. Informacje są odbierane przez router i wykorzystują je do aktualizacji własnej tablicy routingu.Udostępnianie informacji w regularnych odstępach czasu:W ciągu 30 sekund router wysyła informację do sąsiednich routerów.

Algorytm routingu wektora odległości

Niech d_X(y) będzie kosztem najtańszej ścieżki z węzła x do węzła y. Najmniejsze koszty opisuje równanie Bellmana-Forda,

 d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} 

Gdzie minv jest równaniem wziętym dla wszystkich x sąsiadów. Jeśli po podróży od x do v rozważymy najtańszą ścieżkę z v do y, koszt ścieżki wyniesie c(x,v)+d_W(y). Najmniejszy koszt od x do y to minimum c(x,v)+d_W(y) przejął wszystkich sąsiadów.

W przypadku algorytmu routingu wektora odległości węzeł x zawiera następujące informacje o trasie:

• Dla każdego sąsiada v koszt c(x,v) jest kosztem ścieżki od x do bezpośrednio dołączonego sąsiada v.
• Wektor odległości x, tj. D_X= [ D_X(y): y w N], zawierający koszt do wszystkich miejsc docelowych, y, w N.
• Wektor odległości każdego z sąsiadów, tj. D_W= [ D_W(y): y w N ] dla każdego sąsiada v x.

Routing wektora odległości to algorytm asynchroniczny, w którym węzeł x wysyła kopię swojego wektora odległości do wszystkich swoich sąsiadów. Kiedy węzeł x otrzymuje nowy wektor odległości od jednego z sąsiednich wektorów v, zapisuje wektor odległości v i wykorzystuje równanie Bellmana-Forda do aktualizacji własnego wektora odległości. Równanie podano poniżej:

... w Javie

 d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N 

Węzeł x zaktualizował swoją własną tabelę wektorów odległości, korzystając z powyższego równania i wysyła swoją zaktualizowaną tabelę do wszystkich swoich sąsiadów, aby mogli zaktualizować własne wektory odległości.

Algorytm

 At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = &#x221E; for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> 

Uwaga: w algorytmie wektora odległości węzeł x aktualizuje swoją tabelę, gdy albo zauważy jakąkolwiek zmianę kosztów w jednym bezpośrednio połączonym węźle, albo otrzyma aktualizację wektora od jakiegoś sąsiada.

Rozumiemy na przykładzie:

Dzielenie się informacjami

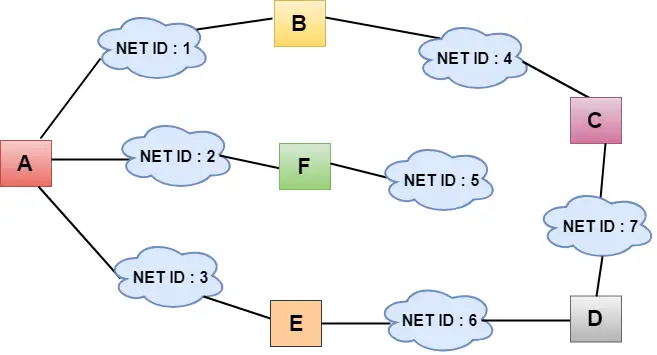
• Na powyższym rysunku każda chmura reprezentuje sieć, a liczba wewnątrz chmury reprezentuje identyfikator sieci.
• Wszystkie sieci LAN są połączone routerami i są reprezentowane w polach oznaczonych jako A, B, C, D, E, F.
• Algorytm routingu wektora odległości upraszcza proces routingu, zakładając, że koszt każdego łącza to jedna jednostka. Dlatego też efektywność transmisji można mierzyć liczbą łączy prowadzących do celu.
• W przypadku routingu wektora odległości koszt opiera się na liczbie przeskoków.

Na powyższym rysunku widzimy, że router wysyła wiedzę do bezpośrednich sąsiadów. Sąsiedzi dodają tę wiedzę do swojej wiedzy i przesyłają zaktualizowaną tabelę do swoich sąsiadów. W ten sposób routery uzyskują własne informacje oraz nowe informacje o sąsiadach.

Tabela routingu

Zachodzą dwa procesy:

• Tworzenie tabeli
• Aktualizacja tabeli

Tworzenie tabeli

Początkowo dla każdego routera tworzona jest tabela routingu, która zawiera co najmniej trzy rodzaje informacji, takie jak identyfikator sieci, koszt i następny przeskok.

Identyfikator sieci:Identyfikator sieciowy określa ostateczne miejsce docelowe pakietu.Koszt:Koszt to liczba przeskoków, które pakiet musi wykonać, aby się tam dostać.Następny skok:Jest to router, do którego pakiet musi zostać dostarczony.

• Na powyższym rysunku pokazano oryginalne tablice routingu wszystkich routerów. W tabeli routingu pierwsza kolumna reprezentuje identyfikator sieci, druga kolumna przedstawia koszt łącza, a trzecia kolumna jest pusta.
• Te tablice routingu są wysyłane do wszystkich sąsiadów.

Na przykład:

 A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A. 

Aktualizacja tabeli

• Kiedy A otrzymuje tablicę routingu od B, wykorzystuje te informacje do aktualizacji tablicy.
• Tabela routingu B pokazuje, w jaki sposób pakiety mogą przemieszczać się do sieci 1 i 4.
• B jest sąsiadem routera A, pakiety od A do B mogą dotrzeć w jednym przeskoku. Zatem do wszystkich kosztów podanych w tabeli B dodaje się 1, a suma będzie kosztem dotarcia do określonej sieci.

• Po dostosowaniu A następnie łączy tę tabelę z własną tabelą, aby utworzyć połączoną tabelę.

• Połączona tabela może zawierać zduplikowane dane. Na powyższym rysunku połączona tabela routera A zawiera zduplikowane dane, dlatego przechowuje tylko te dane, których koszt jest najniższy. Na przykład A może wysłać dane do sieci 1 na dwa sposoby. Pierwszy, który nie korzysta z kolejnego routera, więc kosztuje jeden przeskok. Drugi wymaga dwóch przeskoków (A do B, następnie B do sieci 1). Pierwsza opcja jest najtańsza, dlatego zostaje utrzymana, a druga odrzucona.

• Proces tworzenia tablicy routingu jest kontynuowany dla wszystkich routerów. Każdy router otrzymuje informacje od sąsiadów i aktualizuje tablicę routingu.

Poniżej podano końcowe tablice routingu wszystkich routerów: