Dziel i rządź to wzorzec algorytmiczny. W metodach algorytmicznych projekt polega na podjęciu sporu dotyczącego ogromnego wkładu, podzieleniu go na mniejsze części, rozstrzygnięciu problemu w każdym z małych fragmentów, a następnie połączeniu fragmentarycznych rozwiązań w rozwiązanie globalne. Ten mechanizm rozwiązywania problemu nazywa się strategią dziel i zwyciężaj.

Algorytm „Dziel i rządź” polega na sporze składającym się z trzech następujących kroków.

Dzielićpierwotny problem na zbiór podproblemów.Podbić:Rozwiązuj każdy podproblem indywidualnie, rekurencyjnie.Łączyć:Połącz rozwiązania podproblemów, aby uzyskać rozwiązanie całego problemu.

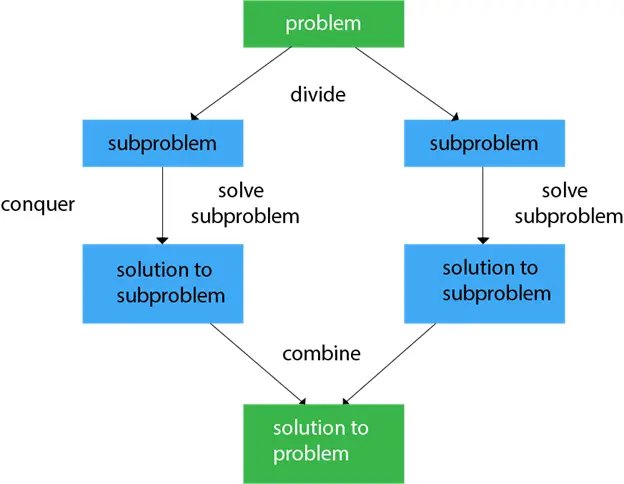
Generalnie możemy podążać za dziel i rządź podejście składające się z trzech etapów.

Przykłady: Specyficzne algorytmy komputerowe opierają się na podejściu Dziel i Rządź:

1. Problem maksymalny i minimalny
2. Wyszukiwanie binarne
3. Sortowanie (sortowanie przez scalanie, sortowanie szybkie)
4. Wieża Hanoi.

Podstawy strategii „Dziel i rządź”:

Istnieją dwie podstawowe zasady strategii „Dziel i rządź”:

1. Formuła relacyjna
2. Warunek zatrzymania

1. Wzór relacyjny: Jest to formuła, którą generujemy na podstawie danej techniki. Po wygenerowaniu Formuły stosujemy Strategię D&C, czyli rozbijamy problem rekurencyjnie i rozwiązujemy zepsute podproblemy.

2. Warunek zatrzymania: Kiedy rozwiązujemy problem za pomocą strategii Dziel i rządź, musimy wiedzieć, przez jaki czas musimy stosować strategię Dziel i rządź. Zatem stan, w którym konieczne jest zatrzymanie kroków rekurencji D&C, nazywany jest stanem zatrzymania.

Zastosowania podejścia „dziel i zwyciężaj”:

Poniższe algorytmy opierają się na koncepcji Techniki Dziel i Rządź:

Wyszukiwanie binarne:Algorytm wyszukiwania binarnego to algorytm wyszukiwania, nazywany także wyszukiwaniem półprzedziałowym lub wyszukiwaniem logarytmicznym. Działa poprzez porównanie wartości docelowej ze środkowym elementem istniejącym w posortowanej tablicy. Jeśli po dokonaniu porównania wartości będą się różnić, wówczas połowa, która nie może zawierać celu, zostanie ostatecznie wyeliminowana, a następnie poszukiwania będą kontynuowane na drugiej połowie. Ponownie rozważymy środkowy element i porównamy go z wartością docelową. Proces jest powtarzany aż do osiągnięcia wartości docelowej. Jeśli po zakończeniu wyszukiwania okaże się, że druga połowa jest pusta, to można stwierdzić, że celu nie ma w tablicy.Szybkie sortowanie:Jest to najbardziej wydajny algorytm sortowania, znany również jako sortowanie przez wymianę partycji. Rozpoczyna się od wybrania wartości przestawnej z tablicy, a następnie podzielenia pozostałych elementów tablicy na dwie podtablice. Podziału dokonuje się poprzez porównanie każdego z elementów z wartością obrotu. Porównuje, czy element ma większą, czy mniejszą wartość niż element przestawny, a następnie sortuje tablice rekurencyjnie.Sortowanie przez scalanie:Jest to algorytm sortowania, który sortuje tablicę poprzez dokonywanie porównań. Rozpoczyna się od podzielenia tablicy na podtablice, a następnie rekurencyjne sortowanie każdej z nich. Po zakończeniu sortowania łączy je z powrotem.Najbliższa para punktów:Jest to problem geometrii obliczeniowej. Algorytm ten kładzie nacisk na znalezienie najbliższej pary punktów w przestrzeni metrycznej, biorąc pod uwagę n punktów, tak aby odległość między parą punktów była minimalna.Algorytm Strassena:Jest to algorytm mnożenia macierzy, którego nazwa pochodzi od Volkera Strassena. Okazało się, że jest znacznie szybszy niż tradycyjny algorytm, gdy działa na dużych macierzach.Algorytm szybkiej transformaty Fouriera Cooleya-Tukeya (FFT):Algorytm szybkiej transformacji Fouriera został nazwany na cześć J. W. Cooleya i Johna Turkeya. Jest to zgodne z podejściem „dziel i zwyciężaj” i narzuca złożoność O(nlogn).Algorytm Karatsuby do szybkiego mnożenia:Jest to jeden z najszybszych algorytmów mnożenia w czasach tradycyjnych, wynaleziony przez Anatolija Karatsubę pod koniec 1960 r. i opublikowany w 1962 r. Mnoży dwie liczby n-cyfrowe w taki sposób, redukując je co najwyżej do jednej cyfry.

Zalety Dziel i rządź

• Dziel i rządź zwykle skutecznie rozwiązuje jeden z największych problemów, takich jak Wieża Hanoi, zagadka matematyczna. Rozwiązywanie skomplikowanych problemów, o których nie ma się podstawowego pojęcia, jest wyzwaniem, ale dzięki podejściu „dziel i zwyciężaj” zmniejsza to wysiłek, ponieważ polega na podzieleniu głównego problemu na dwie połowy, a następnie rozwiązywaniu ich rekurencyjnie. Algorytm ten jest znacznie szybszy niż inne algorytmy.
• Efektywnie wykorzystuje pamięć podręczną, nie zajmując dużo miejsca, ponieważ rozwiązuje proste problemy w obrębie pamięci podręcznej, zamiast uzyskiwać dostęp do wolniejszej pamięci głównej.
• Jest bardziej sprawna niż jej odpowiednik, technika Brute Force.
• Ponieważ algorytmy te hamują równoległość, nie wymaga to żadnych modyfikacji i jest obsługiwany przez systemy obejmujące przetwarzanie równoległe.

Wady dziel i zwyciężaj

• Ponieważ większość algorytmów została zaprojektowana z wykorzystaniem rekurencji, wymaga to dużego zarządzania pamięcią.
• Wyraźny stos może nadużywać przestrzeni.
• Może nawet spowodować awarię systemu, jeśli rekurencja zostanie wykonana na poziomie większym niż stos obecny w procesorze.