Problemy z regresją i klasyfikacją probabilistyczną można rozwiązać za pomocą procesu Gaussa (GP), techniki uczenia się nadzorowanego. Ponieważ każdy proces Gaussa można traktować jako nieskończenie wymiarowe uogólnienie wielowymiarowych Rozkłady Gaussa , w nazwie pojawia się termin Gaussian. W tym poście omówimy procesy Gaussa dotyczące regresji, które są również określane jako regresja procesów Gaussa (GPR). Wiele rzeczywistych problemów z zakresu inżynierii materiałowej, chemii, fizyki i biologii zostało rozwiązanych za pomocą georadaru.
Spis treści
- Regresja procesu Gaussa (GPR)
- Kluczowe pojęcia regresji procesu Gaussa (GPR)
- Matematyczna koncepcja regresji procesu Gaussa (GPR)
- Implementacja procesu Gaussa w Pythonie
Regresja procesu Gaussa (GPR)
Regresja procesu Gaussa (GPR) to potężna i elastyczna technika regresji nieparametrycznej stosowana w nauczanie maszynowe I Statystyka . Jest to szczególnie przydatne przy rozwiązywaniu problemów związanych z danymi ciągłymi, gdzie związek między zmiennymi wejściowymi a wynikami nie jest wyraźnie znany lub może być złożony. GPR to podejście bayesowskie, które może modelować pewność przewidywań, co czyni go cennym narzędziem do różnych zastosowań, w tym optymalizacji, prognozowania szeregów czasowych i nie tylko. GPR opiera się na koncepcji procesu Gaussa, który jest zbiorem zmiennych losowych, których dowolna skończona liczba ma wspólny rozkład Gaussa. Proces Gaussa można traktować jako rozkład funkcji.
Kluczowe pojęcia regresji procesu Gaussa (GPR)
Proces Gaussaina
Nieparametryczny model probabilistyczny zwany a Proces Gaussa (GP) jest wykorzystywany w statystyce i uczeniu maszynowym do regresji, klasyfikacji i kwantyfikacji niepewności. Przedstawia grupę zmiennych losowych, z których każda ma wspólny rozkład Gaussa i może mieć skończoną liczbę. GP to wszechstronna i skuteczna technika modelowania skomplikowanych relacji w danych i tworzenia prognoz obarczonych niepewnością.
Charakterystyka procesów Gaussa :
- Charakter nieparametryczny : Lekarze pierwszego kontaktu mogą dostosować się do złożoności danych, ponieważ nie opierają się na ustalonej liczbie parametrów modelu
- Przewidywania probabilistyczne : Przewidywania lekarzy pierwszego kontaktu można określić ilościowo, ponieważ dostarczają przewidywań w postaci rozkładów prawdopodobieństwa.
- Interpolacja i wygładzanie : GP są przydatne w przypadku zaszumionych lub nieregularnie próbkowanych danych, ponieważ dobrze radzą sobie z wygładzaniem zaszumionych danych i interpolacją między punktami danych.
- Marginalizacja hiperparametrów : Eliminując wymóg jawnego poprawiania hiperparametrów, marginalizują hiperparametry, upraszczając model.
Średnia funkcja
Przewidywana wartość modelowanej funkcji w każdym punkcie wejściowym jest reprezentowana przez średnia funkcja w procesach Gaussa (GP). Funkcjonuje jako podstawowe założenie dotyczące podstawowej struktury danych. Funkcja średniej często jest domyślnie ustawiona na zero, ale niekoniecznie i można ją modyfikować w oparciu o właściwości danych lub wiedzę dziedzinową. Wpływając na centralną tendencję prognoz, pomaga lekarzom pierwszego kontaktu w identyfikowaniu wzorców lub trendów w danych. GP zapewniają prognozy probabilistyczne zawierające niepewność, a także szacunki punktowe poprzez uwzględnienie funkcji średniej
Funkcja kowariancji (jądra).
The funkcja kowariancji , zwana także funkcją jądra, mierzy stopień podobieństwa punktów danych wejściowych do siebie w procesach Gaussa (GP). Jest to istotne przy charakteryzowaniu zachowania modelu GP, wpływając na wybór funkcji z poprzedniego rozkładu. Funkcja kowariancji mierzy podobieństwa parami, aby ustalić korelację między wartościami funkcji. Lekarze pierwszego kontaktu mogą dostosować się do szerokiego zakresu wzorców danych, od gładkich trendów po złożone struktury, ponieważ różne funkcje jądra wychwytują różne rodzaje korelacji. Wybór jądra może w dużym stopniu wpływać na wydajność modelu.
Wcześniejsze dystrybucje
The wcześniejsza dystrybucja w procesach Gaussa (GP) to nasze rozumienie funkcji przed obserwacją jakichkolwiek danych. Zwykle opisuje się ją funkcją kowariancji (jądra) i funkcją średniej. Podczas gdy funkcja kowariancji opisuje podobieństwo lub korelację pomiędzy wartościami funkcji w różnych punktach wejściowych, funkcja średniej koduje nasze wcześniejsze oczekiwania. Jest to wcześniej wykorzystywane przez lekarzy pierwszego kontaktu do tworzenia rozkładu według funkcji. U lekarzy pierwszego kontaktu można wybrać priorytety, aby reprezentować niepewność danych, integrować wiedzę dziedzinową lub wskazywać gładkość.
Rozkłady późniejsze
Procesy Gaussa” późniejsza dystrybucja pokazuje nasze zmienione założenia dotyczące funkcji po obserwacji danych. Łączy prawdopodobieństwo danych, biorąc pod uwagę funkcję i poprzedni rozkład. Regresja tylna w regresji GP zapewnia rozkład funkcji, które najlepiej odpowiadają obserwowanym danym. Uwzględniając przewidywania probabilistyczne i kwantyfikację niepewności, rozkład późniejszy odzwierciedla kompromis między wcześniejszymi przekonaniami przechowywanymi w rozkładzie wcześniejszym a informacjami dostarczonymi przez dane.
Matematyczna koncepcja regresji procesu Gaussa (GPR)
W przypadku zadań regresyjnych stosuje się nieparametryczny, probabilistyczny model uczenia maszynowego zwany regresją procesu Gaussa (GP). Jest to potężne narzędzie do modelowania skomplikowanych i niejednoznacznych interakcji między zmiennymi wejściowymi i wyjściowymi. Zakłada się, że wielowymiarowy rozkład Gaussa generuje punkty danych w regresji GP, a celem jest wywnioskowanie tego rozkładu.
Model regresji GP ma następujące wyrażenie matematyczne. Załóżmy x1, X2,…..,XNsą punktami danych wejściowych, gdzie x należą do liczb rzeczywistych (-2, -1,0,1…), (xI
Załóżmy, że y1, I2,……., INsą wartościami wyjściowymi, gdzie yInależy do liczby rzeczywistej (yI
Model regresji GP zakłada, że proces Gaussa z funkcją średnią (
Następnie dla zbioru lokalizacji testowych x* rozkład f jest określony wzorem:
Zazwyczaj funkcje jądra służą do definiowania funkcji średniej i funkcji kowariancji. Dla ilustracji często stosowane kwadratowe jądro wykładnicze opisano jako:
Gdzie,
k(x_{i}, x_{j}) = Funkcja jądra jest reprezentowana przez to i oblicza korelację lub podobieństwo między dwoma wejściowymi punktami danych, xIi xJ.sigma^2 = Parametr wariancji jądra jest następujący. Ustala skalę funkcji jądra lub rozpiętość pionową. Reguluje stopień korelacji punktów danych. Wyższysigma^2 daje funkcję jądra o większej wariancji.- exp: Funkcja wykładnicza jest odpowiedzialna za podniesienie e do potęgi argumentu.
||x_{i} – x_{j}||^2 : Różnica między wejściowymi punktami danych, xIi xJ, jest kwadratem odległości euklidesowej. Mierzona jest geometryczna separacja pomiędzy punktami w przestrzeni cech.- l2: Jest to reprezentacja skali długości jądra lub długości charakterystycznej. Reguluje tempo, w jakim funkcja jądra pogarsza się w miarę oddalania się punktów danych. Niższe l powoduje szybszą degradację jądra.
Model regresji GP stosuje wnioskowanie bayesowskie w celu określenia rozkładu f, który najprawdopodobniej wygenerował dane, biorąc pod uwagę zestaw danych uczących (x, y). W tym celu należy obliczyć późniejszy rozkład f przy danych, który definiuje się w następujący sposób:
gdzie prawdopodobieństwo krańcowe danych wynosi p(y|x), wcześniejszy rozkład f wynosi p(f), a prawdopodobieństwo danych, biorąc pod uwagę funkcję f, wynosi (y|x,f).
co to jest ini pulpitu
Po poznaniu późniejszego rozkładu f model oblicza późniejszy rozkład predykcyjny w celu uzyskania przewidywań w dodatkowych punktach testowych x*. Można to zdefiniować w następujący sposób:
Gdzie,
p(f^*|x*, y, x) = To pokazuje, biorąc pod uwagę dane szkoleniowe y i x, prawdopodobieństwo warunkowe przewidywanych wartości funkcji f*w nowym punkcie wejściowym x*Inaczej mówiąc, jest to rozkład prawdopodobieństwa dla wszystkich potencjalnych wartości funkcji w nowym miejscu wejściowym x*, uwarunkowane obserwowanymi danymi y i odpowiadającymi im lokalizacjami wejściowymi x.int p(f^*|x^*, f)p(f|y,x)df = W tej części równania zastosowano całkę w celu określenia prawdopodobieństwa warunkowego. Całka obejmuje wszystkie potencjalne wartości funkcji f.p(f^*|x^*, f) = Jest to warunkowy rozkład prawdopodobieństwa oczekiwanych wartości funkcji f*o x*, biorąc pod uwagę wartości funkcji f w niektórych lokalizacjach pośrednich.p(f|y,x) = Biorąc pod uwagę zaobserwowane dane (y) i ich lokalizacje wejściowe (x), jest to warunkowy rozkład prawdopodobieństwa wartości funkcji (f).
W przypadku zadań takich jak podejmowanie decyzji ze świadomością niepewności i aktywne uczenie się rozkład ten stanowi miarę niepewności prognozy, która może być pomocna.
Kroki regresji procesu Gaussa
- Zbieranie danych : Zbierz pary danych wejściowych i wyjściowych dla swojego problemu regresji.
- Wybierz funkcję jądra : Wybierz odpowiednią funkcję kowariancji (jądro), która pasuje do Twojego problemu. Wybór jądra wpływa na kształt funkcji, które GPR może modelować.
- Optymalizacja parametrów : Oszacuj hiperparametry funkcji jądra, maksymalizując prawdopodobieństwo danych. Można tego dokonać za pomocą technik optymalizacyjnych, takich jak opadanie gradientu.
- Prognoza: Biorąc pod uwagę nowe dane wejściowe, użyj przeszkolonego modelu GPR, aby dokonać prognoz. GPR zapewnia zarówno przewidywaną średnią, jak i związaną z nią niepewność (wariancję).
Implementacja regresji procesu Gaussa (GPR)
Pyton import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Wyjście:
W tym kodzie najpierw wygeneruj kilka przykładowych punktów danych z dodanym szumem, a następnie zdefiniuj jądro RBF i utwórz plik Regresor procesu Gaussa z tym. Model jest szkolony na danych szkoleniowych i używany do przewidywania danych testowych. Na koniec wyniki są wizualizowane za pomocą wykresu przedstawiającego dane szkoleniowe, przewidywaną średnią i 95% przedział ufności.
Implementacja procesu Gaussa w Pythonie
Ucz się
Pyton import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Niezbędne biblioteki do regresji procesu Gaussa (GPR) w Pythonie są importowane przez ten kod; to są SciPy dla funkcji algebry liniowej, NumPy do operacji numerycznych i Matplotlib do wizualizacji danych. Aby upewnić się, że jest kompatybilny z niezbędnymi pakietami, dodatkowo weryfikuje wersję Pythona i wypisuje ją wraz z wersjami NumPy i scikit-learn (sklearn).
Wybór jądra
Pyton np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Wyjście:
[RBF(długość_skali=1),
RationalQuadratic(alfa=1, długość_skali=1),
ExpSineSquared(długość_skali=1, okresowość=10),
Iloczyn Kropki(sigma_0=1) ** 2,
Matczyna(długość_skali=1, nu=1,5)]
Kod określa liczbę miejsc testowych (n) i inicjuje a losowe ziarno . Aby wyświetlić wybrane jądra, generuje listę kilku funkcji jądra i drukuje tę listę.
Porównanie i wizualizacja jądra
Pyton for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Wyjście:
RBF
gp.kernel_ RBF(długość_skali=1,93)
gp.log_marginal_likelihood: -3,444937833462133
-------------------------------------------------- -
Racjonalne kwadratowe

gp.kernel_ RationalQuadratic(alfa=1e+05, długość_skali=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
--------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(długość_skali=0,000524, okresowość=2,31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
--------------------------------------------------
Produkt kropkowy

gp.kernel_ DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------
Macierzyński

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------
Kod zaczyna się od zapętlenia różnych funkcji jądra wymienionych na liście kernel_. Regresor procesu Gaussa (gp) jest tworzony przy użyciu określonego jądra dla każdego jądra. W przypadku procesu Gaussa ustala to strukturę kowariancji. Aby ocenić poprzedni rozkład, ustalany jest zbiór testowych punktów wejściowych zwany x_test, o wartościach z zakresu od -5 do 5. Ten zbiór punktów jest przekształcany na wektor kolumnowy.
Za pomocą metody gp.predict w każdym punkcie testowym wyznaczana jest średnia rozkładu apriorycznego (mu_prior) i odchylenie standardowe (sd_prior). Wartości odchylenia standardowego są żądane przy użyciu opcji return_std=True. gp.przykład_y (x_test, 3) służy do uzyskania trzech próbek funkcji z poprzedniej dystrybucji.
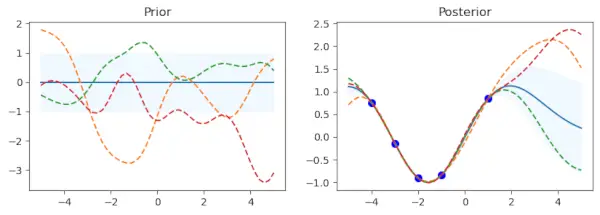
Pierwszy wykres cząstkowy przedstawia średnią poprzedniego rozkładu, z odchyleniem standardowym reprezentowanym przez zacieniony obszar. Próbki nakładają się na siebie w postaci linii przerywanych, a średnia jest wyświetlana w postaci linii ciągłej. Istnieje wątek poboczny o nazwie Prior. Istnieje zdefiniowany zestaw punktów danych treningowych (x_train) i wartości celów (y_train), które są z nimi powiązane. Za pomocą tych punktów dopasowuje się model procesu Gaussa (gp.fit(x_train, y_train)). Dane szkoleniowe w tym kodzie składają się na pięć punktów danych z odpowiadającymi im wartościami sinusoidalnymi.
Po fazie dopasowywania danych uczących procedura oblicza średnią późniejszej dystrybucji (mu_post) i odchylenie standardowe (sd_post) dla tych samych punktów testowych (x_test). gp.sample_y(x_test, 3) jest również używane do tworzenia próbek funkcji z rozkładu późniejszego. Drugi wykres cząstkowy nakłada próbkowane funkcje w postaci linii przerywanych i pokazuje średnią rozkładu późniejszego, zacieniowaną z odchyleniem standardowym. Na niebiesko zaznaczono punkty danych szkoleniowych. Fabuła poboczna nosi nazwę Posterior.
Aby zobaczyć poprzednie i późniejsze wykresy dla bieżącego jądra i uzyskać wizualne zrozumienie zachowania modelu, wywołaj funkcję plt.show() Matplotliba.
Kod pokazuje szczegółowe informacje na temat bieżącego jądra, takie jak gp.kernel_, który wskazuje aktualnie używane jądro, oraz gp.log_marginal_likelihood (gp.kernel_.theta), co daje logarytmowi marginalne prawdopodobieństwo, że model użyje bieżącego jądra, po każdym zestawie wcześniejszych i późniejszych wykresów.
Zalety regresji procesu Gaussa (GPR)
Regresja procesu Gaussa (GPR) ma wiele zalet w różnych zastosowaniach:
- GPR zapewnia probabilistyczne ramy regresji, co oznacza, że nie tylko podaje szacunki punktowe, ale także zapewnia szacunki niepewności prognoz.
- Jest bardzo elastyczny i może uchwycić złożone relacje w danych.
- GPR można dostosować do różnych zastosowań, w tym do prognozowania szeregów czasowych, optymalizacji i optymalizacji Bayesa.
Wyzwania związane z regresją procesu Gaussa (GPR)
- GPR może być kosztowny obliczeniowo w przypadku dużych zbiorów danych, ponieważ wymagane jest odwrócenie macierzy kowariancji.
- Wybór funkcji jądra i jej hiperparametrów może znacząco wpłynąć na wydajność modelu.
Dobre przykłady zastosowań GPR
- Prognoza cen akcji: GPR można wykorzystać do modelowania i przewidywania cen akcji, biorąc pod uwagę zmienność i niepewność na rynkach finansowych.
- Eksperymenty komputerowe: GPR jest przydatny w optymalizacji złożonych symulacji poprzez modelowanie relacji wejście-wyjście i identyfikację najbardziej wpływowych parametrów.
- Wykrywanie anomalii: GPR można zastosować do wykrywania anomalii, gdzie identyfikuje nietypowe wzorce w danych szeregów czasowych poprzez przechwytywanie normalnych rozkładów danych.
Wniosek
Podsumowując, regresja procesu Gaussa jest cennym narzędziem do analizy i przewidywania danych w sytuacjach, w których niezbędne jest zrozumienie niepewności przewidywań. Wykorzystując modelowanie probabilistyczne i funkcje jądra, GPR może zapewnić dokładne i możliwe do interpretacji wyniki. Jednak przy wdrażaniu georadaru w praktyce należy wziąć pod uwagę koszt obliczeniowy i potrzebę udziału ekspertów.
