Metoda zachłanna jest jedną ze strategii takich jak Dziel i rządź, używaną do rozwiązywania problemów. Metodę tę stosuje się do rozwiązywania problemów optymalizacyjnych. Problem optymalizacji to problem, który wymaga maksymalnych lub minimalnych wyników. Rozumiemy za pomocą niektórych terminów.
Metoda zachłanna jest najprostszą i najszybszą metodą. To nie algorytm, ale technika. Główną funkcją tego podejścia jest podejmowanie decyzji na podstawie aktualnie dostępnych informacji. Bez względu na obecne informacje, decyzja jest podejmowana bez obawy o skutki bieżącej decyzji w przyszłości.
wstawianie Pythona
Technikę tę stosuje się zasadniczo do określenia wykonalnego rozwiązania, które może być optymalne lub nie. Rozwiązaniem dopuszczalnym jest podzbiór spełniający podane kryteria. Rozwiązaniem optymalnym jest rozwiązanie, które jest najlepszym i najkorzystniejszym rozwiązaniem w podzbiorze. W przypadku wykonalnych, jeżeli więcej niż jedno rozwiązanie spełnia podane kryteria, wówczas te rozwiązania zostaną uznane za wykonalne, natomiast rozwiązanie optymalne to rozwiązanie najlepsze spośród wszystkich rozwiązań.
Charakterystyka metody zachłannej
Poniżej przedstawiono cechy metody zachłannej:
- Aby skonstruować rozwiązanie w sposób optymalny, algorytm ten tworzy dwa zbiory, z których jeden zawiera wszystkie wybrane elementy, a drugi elementy odrzucone.
- Algorytm zachłanny dokonuje dobrych wyborów lokalnych w nadziei, że rozwiązanie będzie wykonalne lub optymalne.
Składniki algorytmu zachłannego
Elementy, które można wykorzystać w algorytmie zachłannym to:
Java czytaj CSV
Zastosowania algorytmu zachłannego
- Służy do wyszukiwania najkrótszej ścieżki.
- Służy do znalezienia minimalnego drzewa rozpinającego przy użyciu algorytmu Prima lub algorytmu Kruskala.
- Jest używany w sekwencjonowaniu zadań z ostatecznym terminem.
- Algorytm ten służy również do rozwiązywania ułamkowego problemu plecakowego.
Pseudokod algorytmu Greedy
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Powyższy algorytm jest zachłanny. Początkowo rozwiązaniu przypisuje się wartość zerową. W algorytmie zachłannym przekazujemy tablicę i liczbę elementów. Wewnątrz pętli for wybieramy jeden po drugim elementy i sprawdzamy, czy rozwiązanie jest wykonalne, czy nie. Jeśli rozwiązanie jest wykonalne, wykonujemy zjednoczenie.
Rozumiemy na przykładzie.
Załóżmy, że istnieje problem „P”. Chcę podróżować z punktu A do B, jak pokazano poniżej:
P: A → B
Problem w tym, że musimy odbyć tę podróż z A do B. Istnieją różne rozwiązania, aby przejść z A do B. Możemy przejść z A do B poprzez spacer, samochód, rower, pociąg, samolot itp. Istnieje ograniczenie w podróży, że musimy odbyć tę podróż w ciągu 12 godzin. Jeśli pojadę pociągiem lub samolotem tylko wtedy, tę odległość pokonam w ciągu 12 godzin. Istnieje wiele rozwiązań tego problemu, ale tylko dwa rozwiązania spełniają to ograniczenie.
Jeśli mówimy, że musimy pokryć podróż minimalnym kosztem. Oznacza to, że musimy przebyć tę odległość jak najmniej, więc problem ten nazywany jest problemem minimalizacji. Jak dotąd mamy dwa możliwe rozwiązania, tj. jedno koleją i drugie samolotem. Ponieważ podróż pociągiem wiąże się z minimalnymi kosztami, jest to więc rozwiązanie optymalne. Rozwiązanie optymalne to także rozwiązanie wykonalne, ale zapewniające najlepszy wynik, tak aby rozwiązanie było rozwiązaniem optymalnym przy minimalnych kosztach. Optymalne rozwiązanie byłoby tylko jedno.
Problem wymagający wyniku minimalnego lub maksymalnego nazywany jest problemem optymalizacji. Metoda zachłanna jest jedną ze strategii stosowanych w rozwiązywaniu problemów optymalizacyjnych.
waga kat timpf
Wady stosowania algorytmu Greedy
Algorytm zachłanny podejmuje decyzje na podstawie informacji dostępnych na każdym etapie, nie biorąc pod uwagę szerszego problemu. Może zatem istnieć możliwość, że rozwiązanie zachłanne nie zapewni najlepszego rozwiązania każdego problemu.
Na każdym etapie następuje wybór optymalnego lokalnego z zamiarem znalezienia optymalnego globalnego. Rozumiemy na przykładzie.
Rozważmy wykres podany poniżej:
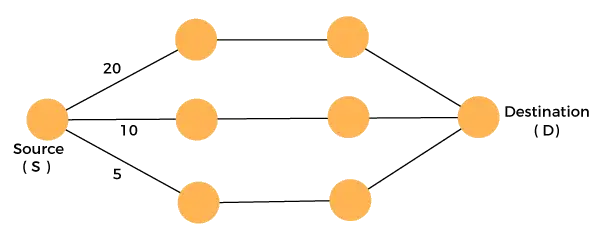
Musimy podróżować od źródła do miejsca docelowego przy minimalnych kosztach. Ponieważ mamy trzy wykonalne rozwiązania ze ścieżkami kosztów 10, 20 i 5. 5 to ścieżka minimalnego kosztu, więc jest to rozwiązanie optymalne. Jest to maksimum lokalne i w ten sposób na każdym etapie znajdujemy maksimum lokalne, aby obliczyć rozwiązanie optymalne globalne.
śpij w javascript
