Kąt mierzony jest w stopniach (°) i radianach. Tworzy się pomiędzy dwoma sąsiednimi bokami wielokąta. Każdy wielokąt ma inne boki i różną liczbę kątów. Wzór na znalezienie kątów w stopniach jest przydatny w geometrii i trygonometrii. Niezbędne jest zrozumienie innych pojęć matematycznych, takich jak łuk, kąt środkowy koła itp.
- Pełny okrąg = 360°
- Linia prosta = 180°
- Półkole = 180°
- Ćwierć koła = 90°
Obliczanie kątów w stopniach
Istnieją trzy różne metody znajdowania kątów w stopniach, które są następujące:
- Korzystanie z ochraniacza D
- Korzystając z twierdzenia Pitagorasa i funkcji trygonometrycznej, można obliczyć trójkąt prostokątny
- Korzystając ze wzoru na sumę kątów
- Kąt środkowy okręgu
Korzystanie z ochraniacza D
Ochraniacz to rodzaj linijki lub skali używanej do pomiaru odległości w centymetrach lub milimetrach. Osłona służąca do pomiaru kątów ma kształt litery „D” z zaznaczoną wartością kątów od 0 do 180° w dowolnym kierunku (prawym lub lewym). Aby zmierzyć kąt, musimy wyrównać oś z linią na literze D. Środkowy okrąg ochraniacza jest wyrównany z wierzchołkiem mierzonego kąta. Promienie wzdłuż wierzchołka kąta pomogą znaleźć kąt w stopniach.
Korzystanie z twierdzenia Pitagorasa i funkcji trygonometrycznych w trójkącie prostokątnym
W trygonometrii istnieje sześć funkcji, sinus, cos, cosec, opalenizna, łóżeczko, I sek. Trójkąt prostokątny ma trzy boki, podstawę, prostopadłą i przeciwprostokątną.
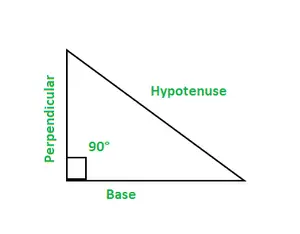
- Podstawa: Jest to bok sąsiadujący z kątem 90°. Prostopadła: Jest to także bok sąsiadujący z kątem 90°. Przeciwprostokątna: Jest to bok przeciwny do kąta 90°.
Trójkąt prostokątny jest reprezentowany przez kąt 90° jako jeden z kątów. Całkowita suma kątów trójkąta wynosi 180°.
- Cosecθ: Jest przedstawiany jako przeciwprostokątna podzielona przez prostopadłą.
Cosecθ =
- Cotθ: Jest reprezentowany jako podstawa podzielona przez prostopadłą.
Łóżeczko θ =
Pozostałe funkcje trygonometryczne są reprezentowane jako:
grzechθ =
Cosθ =
tanθ =
secθ =
Cosecθ można również przedstawić jako 1/sinθ
secθ można również przedstawić jako 1/ cosθ
Cotθ można również przedstawić jako 1/tanθ
Gdzie,
Θ jest kątem
Twierdzenie Pitagorasa
Jeśli znamy dwa boki kąta prostego, możemy łatwo obliczyć trzeci bok trójkąta prostokątnego. W trójkącie prostokątnym twierdzenie Pitagorasa jest dane wzorem:
(Przeciwprostokątna)2= (podstawa)2+ (prostopadle)2
Wzór na sumę kątów
Suma kątów odnosi się do całkowitej sumy kątów wewnętrznych wielokąta tworzącego się między dwoma bokami. Jeśli wielokąt ma sześć boków, istnieje około sześciu kątów. Znalezienie kąta pomaga, jeśli znane są inne kąty i suma kątów wielokąta.
Wzór na obliczenie całkowitej sumy kątów wielokąta wyraża się wzorem:
Całkowita suma kątów = 180 (n – 2)
Gdzie,
n to liczba boków wielokąta
Przykład:
- Jeśli n = 4,

Całkowita suma kątów = 180 (4 – 2)
Słownik C#= 180 (2)
= 360°
Jeśli n = 5,
Całkowita suma kątów = 180 (5 – 2)
= 180 (3)
= 540°
- Jeśli n = 6

Całkowita suma kątów = 180 (6 – 2)
= 180 (4)
= 720°
Kąt środkowy okręgu
Okrąg to okrągła figura, której brzeg znajduje się w równej odległości od jej środka. Odległość między punktem środkowym a granicą nazywa się promieniem okręgu. Kąt utworzony przez dwa promienie okręgu nazywany jest kątem środkowym. Wartość kąta środkowego okręgu mieści się w przedziale od 0 do 360 stopni.

Wzór na obliczenie kąta środkowego okręgu wynika ze wzoru:
Długość łuku = 2πr × (θ/360)
Θ = 360L/2pr
Gdzie,
r jest promieniem okręgu
AB to łuk
Theta to kąt w stopniach.
L = długość łuku
Przykładowe problemy
Pytanie 1: Znajdź kąt środkowy koła o promieniu 2 m i łuku o długości 4 m?
Rozwiązanie :
Wzór na obliczenie kąta środkowego okręgu wynika ze wzoru:
Θ = 360L/2pr
Gdzie,
r jest promieniem okręgu
Theta to kąt w stopniach.
L = długość łuku
Θ = Kąt w stopniach
r = 2 m
Dł. = 4m
Θ = 360 × 4 /2 × π × 2
Θ = 114,6°
przekonwertuj obiekt Java na jsonZatem kąt środkowy okręgu wynosi 114,6°.
Pytanie 2: Znajdź kąt środkowy koła o promieniu 10 cm i łuku o długości 18 cm?
Rozwiązanie :
Wzór na obliczenie kąta środkowego okręgu wynika ze wzoru:
Θ = 360L/2pr
Gdzie,
r jest promieniem okręgu
Theta to kąt w stopniach.
L = długość łuku
r = 10 cm
Dł. = 18 cm
Θ = Kąt w stopniach
Θ = 360 × 18 /2 × π × 10
Θ = 103,13°
Zatem kąt środkowy okręgu wynosi 103,13°.
Pytanie 3: Znajdź kąt równoległoboku, jeśli pozostałe trzy kąty wynoszą 80°, 95° i 105°?
Rozwiązanie :
Linux $home
Równoległobok ma cztery boki, a suma kątów wynosi 360°.
Wzór na sumę kątów = 180 (n – 2)
Gdzie,
n to liczba boków wielokąta
Tutaj n = 4,
Całkowita suma kątów = 180 (4 – 2)
= 180 (2)
= 360°
Suma całkowita = Kąt 1 + Kąt 2 + Kąt 3 + Kąt 4
360 = 80+ 95+ 105+ Kąt 4
360 = 280 + kąt 4
Kąt 4 = 360 – 280
Kąt 4 = 80°
Zadanie 4: Znajdź kąt A na podanym rysunku.

Rozwiązanie :
Dane: Przeciwprostokątna = 12
Prostopadły = 6
Funkcja trygonometryczna służąca do obliczania kąta jest dana wzorem:
grzechA = 6/12
A = 30°
Zadanie 5: Znajdź kąt A na podanym rysunku.

Rozwiązanie :
Dane: Przeciwprostokątna = 10
Podstawa = 5
Funkcja trygonometryczna służąca do obliczania kąta jest dana wzorem:
CosA = 5/10
A = 60°
Pytanie 6: Znajdź kąt pięciokąta, jeśli pozostałe cztery kąty wynoszą 115°, 100°, 105° i 100°?
Rozwiązanie :
W pięciokącie istnieje pięć boków, których łączna suma kątów wynosi 540°.
Wzór na sumę kątów = 180 (n – 2)
normalizacja w bazie danychGdzie,
n to liczba boków wielokąta
Tutaj n = 5,
Całkowita suma kątów = 180 (5 – 2)
= 180 (3)
= 540°
Suma całkowita = Kąt 1 + Kąt 2 + Kąt 3 + Kąt 4 + Kąt 5
540 = 115° + 100° + 105°+100° + Kąt 5
540 = 420 + kąt 5
Kąt 5 = 540 – 420
Kąt 5 = 120°
Zadanie 7: Znajdź kąt A na podanym rysunku.

Rozwiązanie :
Dane: Podstawa = √3
Prostopadły = 1
Funkcja trygonometryczna służąca do obliczania kąta jest dana wzorem:
tanθ =
tanθ = 1/√3
A = 30°
Pytanie 8: Znajdź kąt równoległoboku, jeśli pozostałe trzy kąty wynoszą 100°, 70° i 80°?
Rozwiązanie :
Równoległobok ma cztery boki, których suma kątów wynosi 360°.
Wzór na sumę kątów = 180 (n – 2)
Gdzie,
n to liczba boków wielokąta
Tutaj n = 4,
Całkowita suma kątów = 180 (4 – 2)
= 180 (2)
= 360°
Suma całkowita = Kąt 1 + Kąt 2 + Kąt 3 + Kąt 4
360 = 100 + 70 + 80 + kąt 4
360 = 250 + kąt 4
ciąg do znaku JavaKąt 4 = 360 – 250
Kąt 4 = 110°
Zatem drugi kąt ma miarę 110°.
Pytanie 9: Znajdź kąt sześciokąta, jeśli pozostałych pięć kątów wynosi 120°, 115°, 110°, 125° i 105°?
Rozwiązanie :
Sześciokąt ma sześć boków, a suma kątów wynosi 720°.
Wzór na sumę kątów = 180 (6 – 2)
Gdzie,
n to liczba boków wielokąta
Tutaj n = 6,
Całkowita suma kątów = 180 (6 – 2)
= 180 (4)
= 720°
Suma całkowita = Kąt 1 + Kąt 2 + Kąt 3 + Kąt 4 + Kąt 5 + Kąt 6
720 = 120 + 115 + 110 + 125 + 105 + kąt 6
720 = 575 + kąt 6
Kąt 6 = 720 – 575
Kąt 6 = 145°
Zatem szósty kąt sześciokąta wynosi 145°.






