W tym artykule omówimy przechodzenie wewnętrzne w strukturze danych.
Jeśli chcemy przechodzić przez węzły w kolejności rosnącej, wówczas korzystamy z przechodzenia w kolejności. Poniżej przedstawiono kroki wymagane do przejścia w kolejności:
- Odwiedź wszystkie węzły w lewym poddrzewie
- Odwiedź węzeł główny
- Odwiedź wszystkie węzły w prawym poddrzewie
Liniowe struktury danych, takie jak stos, tablica, kolejka itp., mają tylko jeden sposób przeglądania danych. Ale w hierarchicznych strukturach danych, takich jak drzewo, istnieje wiele sposobów przeglądania danych. Tutaj omówimy inny sposób przechodzenia przez drzewiastą strukturę danych, tj. przechodzenie w kolejności.
Istnieją dwa podejścia stosowane w przypadku przejścia wewnętrznego:
- Przechodzenie w kolejności za pomocą rekurencji
- Przechodzenie wewnątrzrzędne metodą iteracyjną
Technika przechodzenia wewnątrzrzędnego jest zgodna z Lewy rdzeń Prawy polityka. W tym przypadku lewe poddrzewo węzła głównego oznacza, że najpierw przemierzane jest lewe poddrzewo węzła głównego, następnie węzeł główny, a następnie prawe poddrzewo węzła głównego. Tutaj sama nazwa sugeruje, że węzeł główny znajduje się pomiędzy lewym i prawym poddrzewem.
Omówimy przechodzenie wewnątrz rzędu przy użyciu technik rekurencyjnych i iteracyjnych. Zacznijmy najpierw od przechodzenia wewnątrz rzędu za pomocą rekurencji.
Przechodzenie w kolejności za pomocą rekurencji
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Przykład przejścia wewnętrznego
Zobaczmy teraz przykład przejścia wewnątrz rzędu. Procedurę przejścia wewnętrznego będzie łatwiej zrozumieć na przykładzie.
Java do string
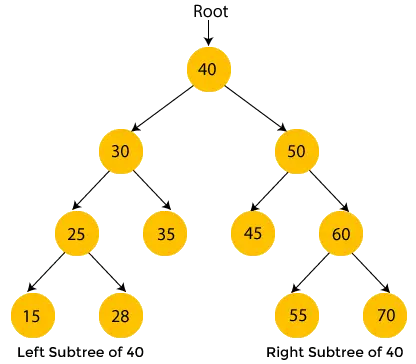
Węzły oznaczone żółtym kolorem nie zostały jeszcze odwiedzone. Teraz będziemy przechodzić przez węzły powyższego drzewa za pomocą przechodzenia w kolejności.
- Tutaj 40 to węzeł główny. Przechodzimy do lewego poddrzewa liczby 40, czyli 30, i ono również ma poddrzewo 25, więc ponownie przechodzimy do lewego poddrzewa liczby 25, czyli 15. Tutaj 15 nie ma poddrzewa, więc wydrukować 15 i przejdź do węzła nadrzędnego, 25.
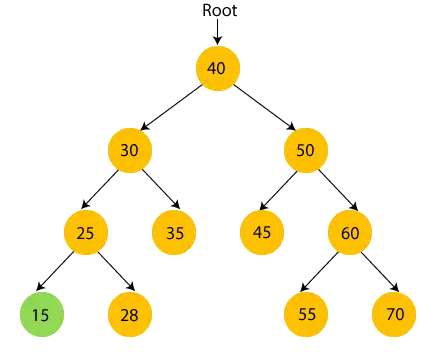
- Teraz, wydrukować 25 i przejdź do prawego poddrzewa liczby 25.
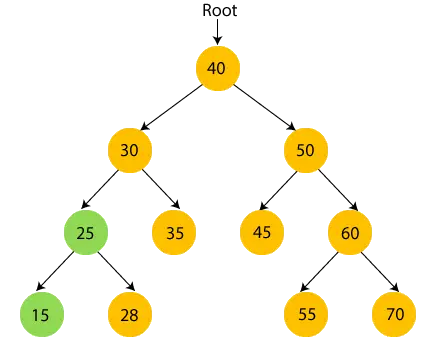
- Teraz, wydrukować 28 i przejdź do węzła głównego liczby 25, czyli liczby 30.
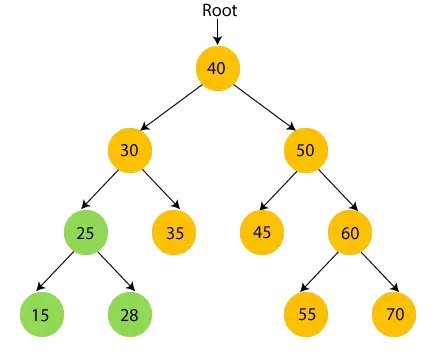
- Zatem odwiedzane jest lewe poddrzewo liczby 30. Teraz, wydrukować 30 i przejdź do prawego dziecka w wieku 30 lat.
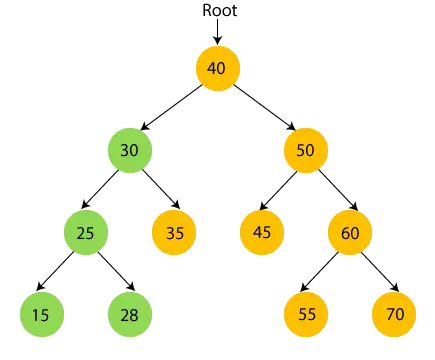
- Teraz, wydrukować 35 i przejdź do węzła głównego 30.
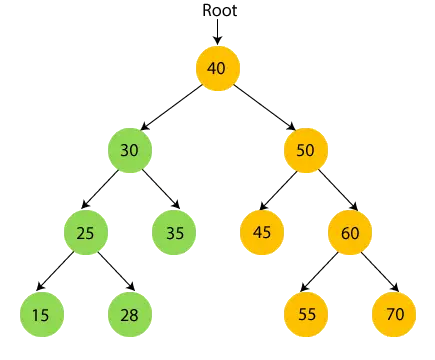
- Teraz, wydrukuj węzeł główny 40 i przejdź do jego prawego poddrzewa.
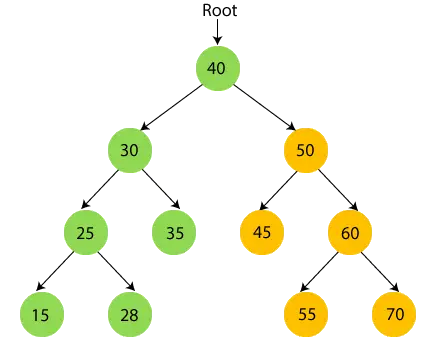
- Teraz rekurencyjnie przechodź przez prawe poddrzewo liczby 40, czyli 50.
50 ma poddrzewo, więc najpierw przejdź przez lewe poddrzewo 50, czyli 45. 45 nie ma dzieci, więc wydrukować 45 i przejdź do jego węzła głównego.
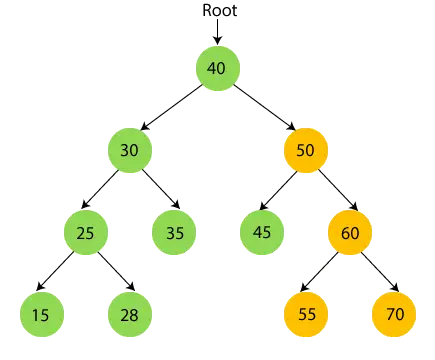
- Teraz wydrukować 50 i przejdź do prawego poddrzewa liczby 50, czyli liczby 60.
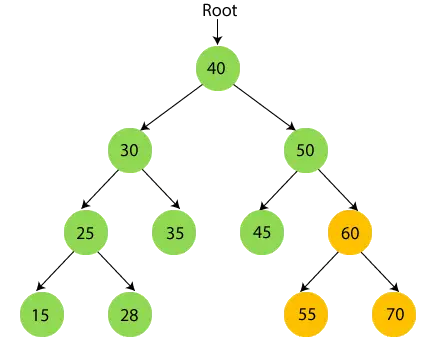
- Teraz rekurencyjnie przechodź przez prawe poddrzewo liczby 50, czyli 60. 60 ma poddrzewo, więc najpierw przejdź przez lewe poddrzewo liczby 60, czyli 55. 55 nie ma dzieci, więc wydrukować 55 i przejdź do jego węzła głównego.
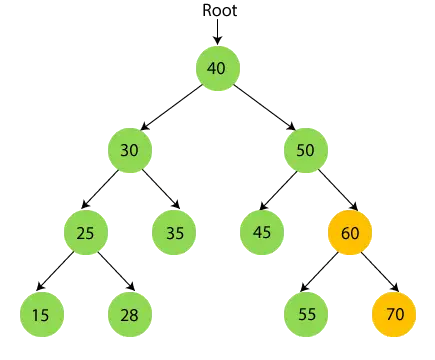
- Teraz wydrukować 60 i przejdź do prawego poddrzewa liczby 60, czyli 70.
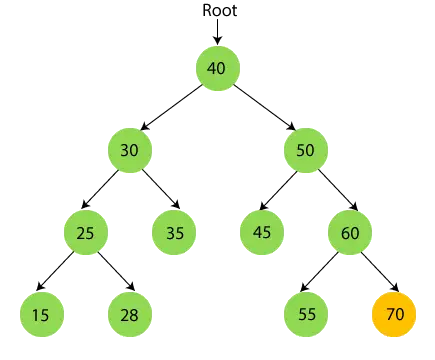
- Teraz wydrukować 70.
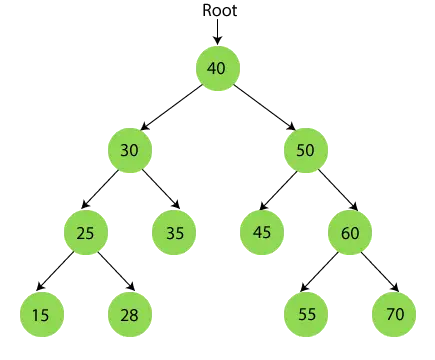
Po zakończeniu przejścia w kolejności ostateczny wynik to -
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Złożoność przejścia Inorder
Złożoność czasowa przejścia Inorder wynosi NA), gdzie „n” jest rozmiarem drzewa binarnego.
Natomiast złożoność przestrzenna przejścia wewnątrz rzędu wynosi O(1), jeśli nie weźmiemy pod uwagę rozmiaru stosu dla wywołań funkcji. W przeciwnym razie złożoność przestrzenna przejścia wewnętrznego wynosi Oh), gdzie „h” jest wysokością drzewa.
Implementacja przejścia Inorder
Przyjrzyjmy się teraz implementacji przechodzenia wewnętrznego w różnych językach programowania.
Program: Napisz program realizujący przechodzenie w kolejności wewnętrznej w języku C.
Ciąg w formacie Java
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Wyjście

Program: Napisz program implementujący przechodzenie w kolejności wewnętrznej w języku C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Wyjście

Program: Napisz program implementujący przechodzenie w kolejności uporządkowanej w Javie.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Wyjście

To tyle na temat artykułu. Mam nadzieję, że artykuł będzie dla Ciebie pomocny i pouczający.











