A Skierowany graf acykliczny , często w skrócie DZIEŃ , to podstawowe pojęcie w teorii grafów. DAG służą do pokazania, w jasny i zorganizowany sposób, jak rzeczy są ze sobą powiązane lub od siebie zależne. W tym artykule dowiemy się o Skierowany graf acykliczny , jego właściwości i zastosowanie w życiu codziennym.

Skierowany graf acykliczny

Co to jest skierowany graf acykliczny?

A Skierowany graf acykliczny (DAG) jest grafem skierowanym, który nie zawiera cykli.

Poniższy wykres przedstawia ukierunkowany graf acykliczny (DAG):

Bezpośredni wykres acykliczny

Znaczenie skierowanego wykresu acyklicznego:

Skierowany graf acykliczny ma dwie ważne cechy:

• Wyreżyserowany Edge S:Na ukierunkowanym grafie acyklicznym, każda krawędź ma kierunek, co oznacza, że ​​przechodzi z jednego wierzchołka (węzła) do drugiego. Kierunek ten oznacza: jednokierunkowa związek lub zależność między węzłami.
• Acykliczny: Termin acykliczny wskazuje, że na wykresie nie ma cykli ani zamkniętych pętli. Innymi słowy, nie można przejść przez sekwencję skierowanych krawędzi i powrócić do tego samego węzła, kierując się kierunkami krawędzi. Tworzenie cykli jest zabronione w DZIEŃ. Dlatego ta cecha jest niezbędna.

Skierowany graf acykliczny

Właściwości skierowanego grafu acyklicznego DAG:

Skierowany graf acykliczny (DAG) ma różne właściwości, dzięki którym można go zastosować w problemach grafowych.

Skierowany graf acykliczny (DAG) ma następujące właściwości:

• Relacja osiągalności: W DAG możemy określić, czy istnieje relacja osiągalności pomiędzy dwoma węzłami. Mówi się, że węzeł A jest osiągalny z węzła B, jeśli istnieje ukierunkowana ścieżka rozpoczynająca się w węźle B i kończąca się w węźle A. Oznacza to, że możesz podążać za kierunkiem krawędzi na wykresie, aby dostać się z B do A.
• Zamknięcie przejściowe: Zamknięcie przechodnie grafu skierowanego to nowy graf, który reprezentuje wszystkie bezpośrednie i pośrednie relacje lub połączenia między węzłami oryginalnego wykresu. Innymi słowy, informuje, do których węzłów można dotrzeć z innych węzłów, podążając za jedną lub większą liczbą skierowanych krawędzi.

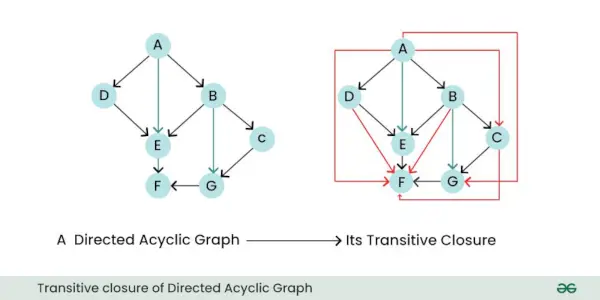
Przechodnie zamknięcie skierowanego grafu acyklicznego

• Redukcja przechodnia: Redukcja przechodnia grafu skierowanego to nowy graf, który zachowuje tylko istotne, bezpośrednie relacje między węzłami, usuwając jednocześnie niepotrzebne krawędzie pośrednie. W istocie upraszcza wykres poprzez eliminację krawędzi, które można wywnioskować z pozostałych krawędzi.

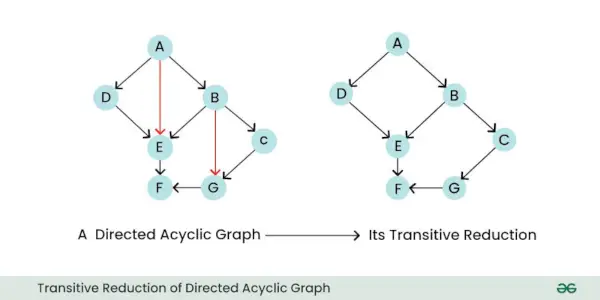
Redukcja przechodnia ukierunkowanego grafu acyklicznego

• Porządek topologiczny: DAG można sortować topologicznie, co oznacza, że ​​można liniowo uporządkować jego węzły w taki sposób, aby dla wszystkich krawędzi węzeł początkowy krawędzi występował wcześniej w sekwencji. Ta właściwość jest przydatna w przypadku zadań takich jak planowanie i rozpoznawanie zależności.

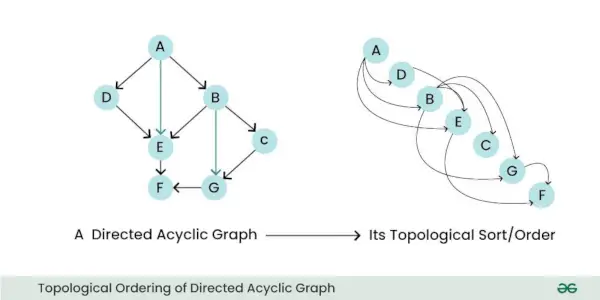
Topologiczne uporządkowanie skierowanego grafu acyklicznego

Praktyczne zastosowania DAG:

• Analiza przepływu danych: W projektowaniu i optymalizacji kompilatora DAG służą do reprezentowania przepływu danych w programie. Pomaga to w optymalizacji kodu poprzez identyfikację zbędnych obliczeń i martwego kodu. DAG są również używane do reprezentowania struktury podstawowe bloki w projektowaniu kompilatorów.

• Harmonogram zadań: DAG są wykorzystywane w zarządzaniu projektami i planowaniu zadań. Każde zadanie lub zadanie jest reprezentowane jako węzeł w DAG, z skierowanymi krawędziami wskazującymi zależności. Acykliczny charakter DAG zapewnia planowanie zadań w logicznym porządku, zapobiegając zależnościom cyklicznym.

Do przedstawienia problemu planowania można zastosować ważony skierowany graf acykliczny. Weźmy przykład problemu z planowaniem zadań. W tym przypadku wierzchołek może reprezentować zadanie, a jego waga może reprezentować rozmiar obliczenia zadania. Podobnie krawędź może reprezentować komunikację między dwoma zadaniami, a jej waga może reprezentować koszt komunikacji:

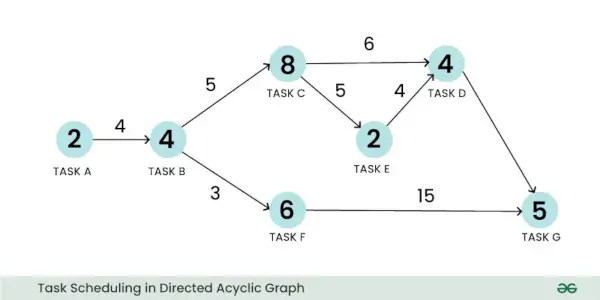
Planowanie zadań w ukierunkowanym grafie acyklicznym

Wniosek:

Podsumowując, kierowane grafy acykliczne są podstawową koncepcją teorii grafów z licznymi zastosowaniami praktycznymi. DAG odgrywają kluczową rolę w planowaniu zadań, analizie przepływu danych, rozwiązywaniu zależności i różnych innych obszarach informatyki i inżynierii. Pomagają optymalizować procesy, zarządzać zależnościami i zapewniać efektywną realizację zadań lub zadań.