Długość, szerokość i wysokość to wymiary figury geometrycznej, które wskazują, jak długa, szeroka i wysoka jest ta figura. Długość, szerokość i wysokość są ważnymi narzędziami w przypadku figur geometrycznych.

W tym artykule poznasz wszystkie szczegóły związane z długością, szerokością i wysokością. Jeśli jesteś prawdziwym studentem i ciekawi Cię długość, szerokość i wysokość, to jesteś we właściwym miejscu.

Spis treści

• Co to jest długość szerokość wysokość?
• Jak zapisać wymiary długości, szerokości, wysokości
• Długość × szerokość × wysokość
• Długość kontra szerokość
• Długość, szerokość i wysokość w prostokącie
• Długość Szerokość Wysokość Wzór

Co to jest długość szerokość wysokość?

Długość, szerokość i wysokość służą do znajdowania boku lub wymiarów obiektu. Najdłuższy bok figury to długość, szerokość to krótszy bok figury, a pionowy wymiar figury nazywany jest wysokością. Długość i szerokość stosujemy w kształtach dwuwymiarowych (kształty 2D), natomiast w kształtach trójwymiarowych (kształty 3D) używamy wysokości wraz z długością i szerokością.

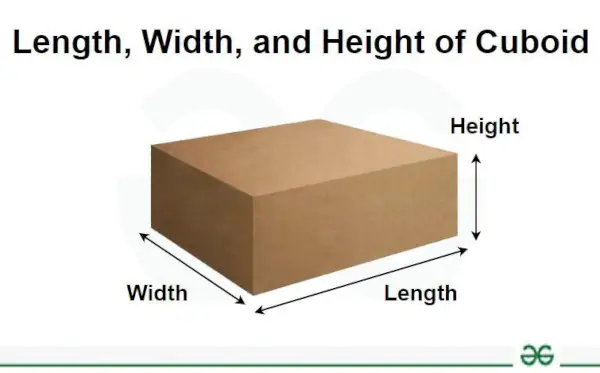
Długość

Narzędzie wymagające pomiaru odległości między dwoma punktami nazywa się Długość. Długość służy do pomiaru najdłuższego wymiaru figury. Długość jest miarą liniową, która służy do pomiaru jedynie odległości dzielącej dwa punkty. Jednostki długości to metry, kilometry, centymetry, cale i tak dalej.

Jako przykład długości możemy powiedzieć, że długość boiska do krykieta wynosi 20 metrów.

Szerokość

Narzędzie używane do pomiaru krótszej odległości obiektu lub figury nazywa się Szerokość. Jest to krótszy wymiar figury. Szerokość jest miarą liniową, która służy do pomiaru tylko krótszej odległości obiektu. Jednostką szerokości są metry, kilometry, centymetry, cale i tak dalej.

Jako przykład szerokości możemy powiedzieć, że szerokość boiska do krykieta wynosi 5 metrów.

Wysokość

Innym określeniem wysokości jest głębokość. Wysokość lub głębokość to trzeci pionowy wymiar obiektu w kształcie 3D. Określa głębokość lub wysokość obiektu. Jednostki wzrostu to metry, kilometry, centymetry, cale i tak dalej.

Jak zapisać wymiary długości, szerokości, wysokości

Wymiary długości, szerokości i wysokości można zapisać bardzo łatwo, ponieważ zapoznaliśmy się już z definicją tych narzędzi. W kształcie geometrycznym 2D otrzymujemy tylko dwa wymiary, długość i szerokość (szerokość). W kształcie 3D otrzymujemy wszystkie trzy wymiary: długość, szerokość i wysokość. Najdłuższy bok figury jest oznaczony jako długość. Wymiar pionowy zapisywany jest jako wysokość lub głębokość. Pozostała strona nazywana jest szerokością lub szerokością.

Koncepcja ta została przedstawiona na powyższym schemacie. Jednostki tych wymiarów są wyrażane w jednostkach takich jak metry, centymetry, cale i tak dalej.

Długość × szerokość × wysokość

Kiedy wszystkie trzy wymiary pomnożymy razem, otrzymamy objętość o kształcie geometrycznym. Objętość definiuje się jako ilość przestrzeni zajmowanej przez kształt geometryczny. The objętość prostopadłościanu jest równa pomnożeniu jego długości, szerokości i wysokości. Innymi słowy, jeśli pomnożymy wszystkie trzy wymiary przez siebie, otrzymamy objętość prostopadłościanu lub dowolnego prostokąta.

Matematycznie objętość prostopadłościanu ( prostopadłościan ) lub Pudełko = Długość × Szerokość × Wysokość.

Na przykład, jeśli długość, szerokość i wysokość prostopadłościanu wynosi odpowiednio 5, 8 i 10 jednostek, to jego objętość (V) wynosi:

V = 5 × 8 × 10

V = 400 jednostek sześciennych

sieciowy system operacyjny

Długość kontra szerokość

Długość i szerokość służą do pomiaru odległości lub wymiaru boku, ale istnieje między nimi znacząca różnica. Długość to najdłuższy wymiar, szerokość to najkrótszy wymiar. Długość jest zawsze większa niż szerokość. Innymi słowy, długość oznacza dłuższy bok figury, a szerokość oznacza jej krótszy bok. Szerokość (szerokość) nadaje szeroki charakter kształtu geometrycznego, natomiast długość określa długość kształtu.

Jeśli dane są dwa wymiary kształtu geometrycznego, czyli odpowiednio 100 cm i 70 cm, to z łatwością możemy powiedzieć, że 100 cm to długość, a 70 cm to szerokość.

Długość, szerokość i wysokość w prostokącie

Prostokąt jest przykładem kształtu 2D, więc ma tylko długość i szerokość, ale prostokątne pudełko lub prostokątny pryzmat (prostopadłościan) ma kształt 3D, więc ma wszystkie trzy wymiary: długość, szerokość i wysokość. Można więc powiedzieć, że przedłużenia kształtu prostokątnego w 3D zawierają długość, szerokość i wysokość.

Długość Szerokość Wysokość Wzór

Długość, szerokość i wysokość służą do obliczania objętości i pola powierzchni prostopadłościanu za pomocą określonych wzorów. Poniżej podano te formuły,

Objętość prostopadłościanu Formuła

Objętość prostopadłościanu = długość × szerokość × wysokość

Pole powierzchni prostopadłościanu Formuła

Pole powierzchni bocznej prostopadłościanu = 2 [(długość × szerokość) + (szerokość × wysokość)]

Całkowita powierzchnia prostopadłościanu = 2 [(długość × szerokość) + (szerokość × wysokość) + (długość × wysokość)]

Długość Szerokość Wysokość pudełka

Długość, szerokość i wysokość pudełka można łatwo wyrazić, patrząc na jego kształt. Ponieważ wiemy, że długość pudełka to zazwyczaj najdłuższy bok, jego szerokość to krótszy bok, a jego wysokość to wymiar w wymiarze pionowym.

Generalnie dla dowolnych kształtów 3D wymiary są zapisywane jako Długość, po której następuje Szerokość lub Szerokość i Wysokość. Oznacza to, że jeśli mamy zmierzyć wymiary pudełka, to należy je podać jako długość, szerokość i wysokość. Na przykład 10 metrów, 5 metrów i 8 metrów oznacza:

• Długość pudełka = 10 metrów
• Szerokość pudełka = 5 metrów
• Wysokość pudełka = 8 metrów

Podobne artykuły,

• Obszar kształtów 2D
• Powierzchnia i objętość kształtów 3D

Długość Szerokość Wysokość Przykłady

Oto niektóre przykłady dotyczące długości, szerokości i wysokości:

Przykład 1: Wymiary prostokątnego ogrodu 2D to 50 metrów i 35 metrów. Jaki jest wymiar długości i szerokości?

Rozwiązanie:

Jak wiemy,

samouczek języka programowania Java

Dłuższy wymiar jest ogólnie uważany za długość, a krótszy za szerokość

Wymiar długości wynosi 50 metrów, a szerokość 35 metrów

Przykład 2: Jeśli wymiary prostokątnego pudełka wynoszą odpowiednio 26 m, 22 m i 24 m. Jaka będzie wartość wysokości tego prostokątnego pudełka?

Rozwiązanie:

Jak wiemy, wymiary w kształcie 3D wyrażane są w kolejności długości, szerokości i wysokości.

Podane wymiary,

• Długość = 26 m
• Szerokość = 22 m
• Wysokość = 24 m

Zatem wysokość wynosi 24 metry

Przykład 3: Długość, szerokość i wysokość prostopadłościanu wynosi 6 cm, 4 cm i 5 cm. Określ jego objętość.

Rozwiązanie:

Dany,

• Długość = 6 cm
• Szerokość = 4 cm
• Wysokość = 5 cm

Objętość = długość × szerokość × wysokość

Objętość = 6 × 4 × 5

Objętość = 120 cm3

Ćwicz pytania dotyczące długości, szerokości, wysokości

Niektóre pytania praktyczne dotyczące długości, szerokości i wysokości to:

Pytanie 1: Znajdź objętość prostopadłościanu o długości, szerokości i wysokości jako: długość = 12 cm, szerokość = 8 cm, wysokość = 4 cm.

Pytanie 2: Znajdź objętość prostopadłościanu o długości, szerokości i wysokości jako: długość = 18 m, szerokość = 9 m, wysokość = 3 m.

Pytanie 3: Znajdź TSA prostopadłościanu o długości, szerokości i wysokości jako: długość = 42 cm, szerokość = 28 cm, wysokość = 14 cm.

Pytanie 4: Znajdź LSA prostopadłościanu o długości, szerokości i wysokości jako: długość = 7 cm, szerokość = 5 cm, wysokość = 6 cm.

Często zadawane pytania dotyczące długości, szerokości, wysokości

Co to jest długość szerokość wysokość?

Długość, szerokość i wysokość to narzędzia używane do pomiaru wymiarów różnych obiektów trójwymiarowych.

Który wymiar jest dłuższy między szerokością a długością?

Długość to dłuższy wymiar. Długość jest powszechnie używana do pomiaru dłuższych wymiarów obiektu.

Co stanie się z wymiarem, jeśli obiekt będzie okrągły, jak kula?

Do różnych pomiarów obiektów takich jak kule używamy promienia lub średnicy zamiast długości, szerokości lub wysokości, jeśli obiekt jest okrągły. „Wysokość” kuli jest równa jej średnicy.

Czy objętość jest zawsze obliczana na podstawie długości wzoru × szerokość × wysokość?

Formuła objętości to ogólnie długość × szerokość × wysokość dla kształtów 3-D, gdzie jej wymiary to długość, szerokość i wysokość.