Regresja liniowa i regresja logistyczna to dwa słynne algorytmy uczenia maszynowego, które wchodzą w zakres techniki uczenia się nadzorowanego. Ponieważ oba algorytmy mają charakter nadzorowany, algorytmy te wykorzystują oznaczony zbiór danych do przewidywania. Ale główna różnica między nimi polega na tym, jak są używane. Regresja liniowa służy do rozwiązywania problemów regresji, natomiast regresja logistyczna służy do rozwiązywania problemów klasyfikacji. Poniżej znajduje się opis obu algorytmów wraz z tabelą różnic.
Regresja liniowa:
- Regresja liniowa to jeden z najprostszych algorytmów uczenia maszynowego wchodzącego w skład techniki uczenia się nadzorowanego i wykorzystywanego do rozwiązywania problemów regresyjnych.
- Służy do przewidywania ciągłej zmiennej zależnej za pomocą zmiennych niezależnych.
- Celem regresji liniowej jest znalezienie najlepszej linii dopasowania, która pozwala dokładnie przewidzieć wynik dla ciągłej zmiennej zależnej.
- Jeśli do przewidywania używana jest pojedyncza zmienna niezależna, nazywa się to prostą regresją liniową, a jeśli istnieją więcej niż dwie zmienne niezależne, taką regresję nazywa się wielokrotną regresją liniową.
- Znajdując najlepszą linię dopasowania, algorytm ustala związek pomiędzy zmienną zależną i zmienną niezależną. A zależność powinna mieć charakter liniowy.
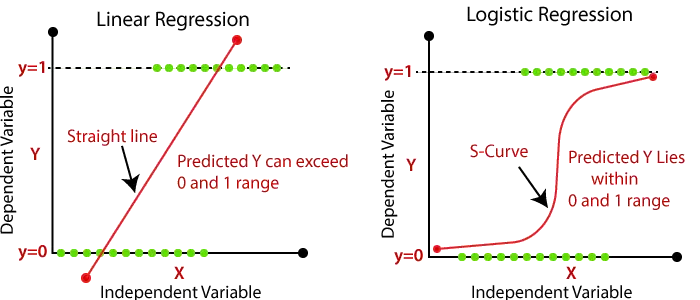
- Wynikiem regresji liniowej powinny być tylko wartości ciągłe, takie jak cena, wiek, wynagrodzenie itp. Związek między zmienną zależną a zmienną niezależną można pokazać na poniższym obrazku:

Na powyższym obrazku zmienna zależna znajduje się na osi Y (wynagrodzenie), a zmienna niezależna na osi X (doświadczenie). Linię regresji można zapisać jako:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Gdzie0i a1są współczynnikami, a ε jest składnikiem błędu.
Regresja logistyczna:
- Regresja logistyczna jest jednym z najpopularniejszych algorytmów uczenia maszynowego wchodzącego w skład technik uczenia nadzorowanego.
- Może być stosowany do problemów klasyfikacyjnych i regresyjnych, ale głównie jest używany do problemów klasyfikacyjnych.
- Regresja logistyczna służy do przewidywania kategorycznej zmiennej zależnej za pomocą zmiennych niezależnych.
- Wynik problemu regresji logistycznej może wynosić tylko od 0 do 1.
- Regresję logistyczną można zastosować, gdy wymagane jest prawdopodobieństwo między dwiema klasami. Na przykład, czy dzisiaj będzie padać deszcz, czy nie, 0 lub 1, prawda czy fałsz itp.
- Regresja logistyczna opiera się na koncepcji estymacji maksymalnego prawdopodobieństwa. Według tego szacunku zaobserwowane dane powinny być najbardziej prawdopodobne.
- W regresji logistycznej ważoną sumę danych wejściowych przekazujemy przez funkcję aktywacji, która może odwzorowywać wartości pomiędzy 0 a 1. Taka funkcja aktywacji jest nazywana funkcja sigmoidalna a uzyskana krzywa nazywana jest krzywą sigmoidalną lub krzywą S. Rozważ poniższy obraz:

- Równanie regresji logistycznej wygląda następująco:

Różnica między regresją liniową a regresją logistyczną:
| Regresja liniowa | Regresja logistyczna |
|---|---|
| Regresja liniowa służy do przewidywania ciągłej zmiennej zależnej przy użyciu danego zestawu zmiennych niezależnych. | Regresja logistyczna służy do przewidywania jakościowej zmiennej zależnej przy użyciu danego zestawu zmiennych niezależnych. |
| Regresja liniowa służy do rozwiązywania problemów regresji. | Regresja logistyczna jest wykorzystywana do rozwiązywania problemów klasyfikacyjnych. |
| W regresji liniowej przewidujemy wartość zmiennych ciągłych. | W regresji logistycznej przewidujemy wartości zmiennych kategorycznych. |
| W regresji liniowej znajdujemy linię najlepszego dopasowania, dzięki której możemy łatwo przewidzieć wynik. | W regresji logistycznej znajdujemy krzywą S, według której możemy klasyfikować próbki. |
| Do szacowania dokładności stosowana jest metoda estymacji najmniejszych kwadratów. | Do oceny dokładności wykorzystuje się metodę estymacji największej wiarygodności. |
| Dane wyjściowe regresji liniowej muszą być wartością ciągłą, taką jak cena, wiek itp. | Wynikiem regresji logistycznej musi być wartość kategoryczna, taka jak 0 lub 1, tak lub nie itp. |
| W regresji liniowej wymagane jest, aby związek między zmienną zależną a zmienną niezależną był liniowy. | W regresji logistycznej nie jest wymagane występowanie liniowej zależności pomiędzy zmienną zależną i niezależną. |
| W regresji liniowej może występować kolinearność pomiędzy zmiennymi niezależnymi. | W regresji logistycznej nie powinna występować kolinearność między zmienną niezależną. |
