Algorytm Luhna, znany również jako moduł 10 Lub w kierunku 10 algorytm to prosta formuła sumy kontrolnej używana do sprawdzania poprawności różnych numerów identyfikacyjnych, takich jak numery kart kredytowych, numery IMEI, kanadyjskie numery ubezpieczenia społecznego. Wzór LUHN został stworzony pod koniec lat 60. XX wieku przez grupę matematyków. Wkrótce potem przyjęły to firmy obsługujące karty kredytowe. Ponieważ algorytm jest własnością publiczną, może z niego korzystać każdy. Większość kart kredytowych i wiele rządowych numerów identyfikacyjnych wykorzystuje ten algorytm jako prostą metodę odróżniania prawidłowych numerów od błędnie wpisanych lub z innych powodów niepoprawnych. Został zaprojektowany w celu ochrony przed przypadkowymi błędami, a nie złośliwymi atakami.
Kroki związane z algorytmem Luhna
Przyjrzyjmy się algorytmowi na przykładzie:
Rozważmy przykład numeru konta 79927398713 .
Krok 1 – Zaczynając od prawej cyfry, podwajaj wartość co drugiej cyfry,
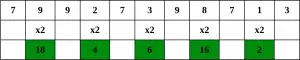
Krok 2 – Jeżeli podwojenie liczby daje liczbę dwucyfrową, czyli większą od 9 (np. 6 × 2 = 12), to dodajemy cyfry iloczynu (np. 12: 1 + 2 = 3, 15: 1 + 5 = 6), aby uzyskać liczbę jednocyfrową.

Krok 3 – Teraz zsumuj wszystkie cyfry.
topologie

Krok 4 – Jeżeli suma modulo 10 jest równa 0 (jeśli suma kończy się na zera), to liczba jest ważna zgodnie ze wzorem Luhna; w przeciwnym razie jest to nieważne.

Ponieważ suma wynosi 70, co jest wielokrotnością 10, numer konta jest prawdopodobnie prawidłowy.
Pomysł jest prosty; przechodzimy od końca. Co drugą cyfrę podwajamy przed dodaniem. Do liczby otrzymanej po podwojeniu dodajemy dwie cyfry.
Realizacja:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; ja--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Jawa
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
funkcje łańcuchowe Java
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
schemat modelu e-r
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; ja--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
przekreślenie przeceny
>
JavaScript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; ja--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Wyjście
This is a valid card>
Algorytm Luhna wykrywa każdy błąd jednocyfrowy, a także prawie wszystkie transpozycje sąsiednich cyfr.
