W prawdziwym świecie nauczanie maszynowe zastosowaniach często występuje wiele istotnych funkcji, ale można zaobserwować tylko ich podzbiór. Kiedy mamy do czynienia ze zmiennymi, które czasami są obserwowalne, a czasami nie, rzeczywiście możliwe jest wykorzystanie przypadków, w których zmienna jest widoczna lub zaobserwowana, w celu uzyskania wiedzy i przewidywania przypadków, w których nie jest ona obserwowalna. Podejście to jest często określane jako obsługa brakujących danych. Wykorzystując dostępne instancje, w których zmienna jest obserwowalna, algorytmy uczenia maszynowego mogą uczyć się wzorców i relacji na podstawie obserwowanych danych. Te wyuczone wzorce można następnie wykorzystać do przewidywania wartości zmiennej w przypadkach, gdy jej brakuje lub nie można jej zaobserwować.
Algorytm maksymalizacji oczekiwań można zastosować do obsługi sytuacji, w których zmienne są częściowo obserwowalne. Kiedy pewne zmienne są obserwowalne, możemy wykorzystać te przypadki do poznania i oszacowania ich wartości. Wtedy możemy przewidzieć wartości tych zmiennych w przypadkach, gdy nie jest to obserwowalne.
Algorytm EM został zaproponowany i nazwany w przełomowym artykule opublikowanym w 1977 roku przez Arthura Dempstera, Nan Laird i Donalda Rubina. Ich praca sformalizowała algorytm i wykazała jego przydatność w modelowaniu statystycznym i estymacji.
Algorytm EM ma zastosowanie do zmiennych ukrytych, czyli zmiennych, których nie można bezpośrednio zaobserwować, ale można je wywnioskować z wartości innych obserwowanych zmiennych. Wykorzystując znaną ogólną postać rozkładu prawdopodobieństwa regulującego te ukryte zmienne, algorytm EM może przewidzieć ich wartości.
Algorytm EM służy jako podstawa dla wielu algorytmów klastrowania bez nadzoru w dziedzinie uczenia maszynowego. Zapewnia ramy do znajdowania lokalnych parametrów największej wiarygodności modelu statystycznego i wnioskowania o zmiennych ukrytych w przypadkach, gdy brakuje danych lub są one niekompletne.
Algorytm maksymalizacji oczekiwań (EM).
Algorytm maksymalizacji oczekiwań (EM) to iteracyjna metoda optymalizacji, która łączy różne metody optymalizacji bez nadzoru nauczanie maszynowe algorytmy do znajdowania maksymalnego prawdopodobieństwa lub maksymalnych późniejszych szacunków parametrów w modelach statystycznych obejmujących nieobserwowane zmienne ukryte. Algorytm EM jest powszechnie używany w przypadku modeli zmiennych ukrytych i może obsługiwać brakujące dane. Składa się z etapu estymacji (etap E) i etapu maksymalizacji (etap M), tworząc proces iteracyjny mający na celu poprawę dopasowania modelu.
- W kroku E algorytm oblicza zmienne ukryte, czyli oczekiwanie logarytmu wiarygodności, na podstawie bieżących estymatorów parametrów.
- W kroku M algorytm wyznacza parametry, które maksymalizują oczekiwaną logarytywność uzyskaną w kroku E, a odpowiednie parametry modelu są aktualizowane w oparciu o oszacowane zmienne ukryte.

Maksymalizacja oczekiwań w algorytmie EM
Powtarzając te kroki, algorytm EM stara się maksymalizować prawdopodobieństwo zaobserwowanych danych. Jest powszechnie używany do zadań uczenia się bez nadzoru, takich jak grupowanie, w których wnioskuje się ukryte zmienne, i ma zastosowania w różnych dziedzinach, w tym w uczeniu maszynowym, widzeniu komputerowym i przetwarzaniu języka naturalnego.
instrukcja bash if
Kluczowe terminy w algorytmie maksymalizacji oczekiwań (EM).
Niektóre z najczęściej używanych kluczowych terminów w algorytmie maksymalizacji oczekiwań (EM) są następujące:
- Zmienne ukryte: Zmienne ukryte to zmienne nieobserwowane w modelach statystycznych, które można wywnioskować jedynie pośrednio na podstawie ich wpływu na zmienne obserwowalne. Nie można ich bezpośrednio zmierzyć, ale można je wykryć poprzez ich wpływ na obserwowalne zmienne. Prawdopodobieństwo: Jest to prawdopodobieństwo zaobserwowania danych danych przy danych parametrach modelu. W algorytmie EM celem jest znalezienie parametrów maksymalizujących prawdopodobieństwo. Log-Likelihood: Jest to logarytm funkcji wiarygodności, która mierzy stopień dopasowania obserwowanych danych do modelu. Algorytm EM stara się maksymalizować logarytm wiarygodności. Estymacja maksymalnej wiarygodności (MLE): MLE to metoda estymacji parametrów modelu statystycznego poprzez znalezienie wartości parametrów, które maksymalizują funkcję wiarygodności, która mierzy, jak dobrze model wyjaśnia obserwowane dane. Prawdopodobieństwo późniejsze: W kontekście wnioskowania bayesowskiego algorytm EM można rozszerzyć, aby oszacować maksymalne oszacowania a posteriori (MAP), gdzie prawdopodobieństwo późniejsze parametrów jest obliczane na podstawie rozkładu apriorycznego i funkcji wiarygodności. Krok oczekiwań (E): Krok E algorytmu EM oblicza oczekiwaną wartość lub późniejsze prawdopodobieństwo ukrytych zmiennych, biorąc pod uwagę obserwowane dane i bieżące oszacowania parametrów. Polega na obliczeniu prawdopodobieństw każdej ukrytej zmiennej dla każdego punktu danych. Krok maksymalizacji (M): Krok M algorytmu EM aktualizuje estymatory parametrów poprzez maksymalizację oczekiwanej logarytmu wiarygodności uzyskanej z etapu E. Polega na znalezieniu wartości parametrów, które optymalizują funkcję wiarygodności, zwykle za pomocą metod optymalizacji numerycznej. Zbieżność: Zbieżność odnosi się do stanu, w którym algorytm EM osiągnął stabilne rozwiązanie. Zwykle określa się ją poprzez sprawdzenie, czy zmiana logarytmu wiarygodności lub oszacowań parametrów spada poniżej z góry określonego progu.
Jak działa algorytm maksymalizacji oczekiwań (EM):
Istotą algorytmu maksymalizacji oczekiwań jest wykorzystanie dostępnych danych obserwowanych ze zbioru danych do oszacowania brakujących danych, a następnie wykorzystanie tych danych do aktualizacji wartości parametrów. Przyjrzyjmy się szczegółowo algorytmowi EM.

Schemat blokowy algorytmu EM
- Inicjalizacja:
- Początkowo rozważany jest zbiór wartości początkowych parametrów. Do systemu podawany jest zbiór niekompletnych zaobserwowanych danych przy założeniu, że obserwowane dane pochodzą z konkretnego modelu.
- Oblicz późniejsze prawdopodobieństwo lub odpowiedzialność każdej ukrytej zmiennej, biorąc pod uwagę zaobserwowane dane i bieżące szacunki parametrów.
- Oszacuj brakujące lub niekompletne wartości danych, korzystając z bieżących szacunków parametrów.
- Oblicz logarytm wiarygodności zaobserwowanych danych w oparciu o bieżące szacunki parametrów i szacunkowe brakujące dane.
- Zaktualizuj parametry modelu, maksymalizując oczekiwaną wiarygodność pełnego logu danych uzyskaną z etapu E.
- Zwykle wiąże się to z rozwiązywaniem problemów optymalizacyjnych w celu znalezienia wartości parametrów, które maksymalizują logarytm wiarygodności.
- Konkretna zastosowana technika optymalizacji zależy od charakteru problemu i używanego modelu.
- Sprawdź zbieżność, porównując zmianę logarytmu wiarygodności lub wartości parametrów pomiędzy iteracjami.
- Jeśli zmiana jest poniżej z góry określonego progu, zatrzymaj się i uznaj, że algorytm jest zbieżny.
- W przeciwnym razie wróć do kroku E i powtarzaj proces, aż do osiągnięcia zbieżności.
Wdrożenie algorytmu maksymalizacji oczekiwań krok po kroku
Zaimportuj niezbędne biblioteki
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
jak zainicjować tablicę w Javie
>
>
Wygeneruj zbiór danych z dwoma składnikami Gaussa
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
operatory Javy
>
Wyjście :

Wykres gęstości
Zainicjuj parametry
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Wykonaj algorytm EM
- Iteruje po określonej liczbie epok (w tym przypadku 20).
- W każdej epoce krok E oblicza obowiązki (wartości gamma), oceniając gęstości prawdopodobieństwa Gaussa dla każdego składnika i ważąc je odpowiednimi proporcjami.
- Krok M aktualizuje parametry poprzez obliczenie średniej ważonej i odchylenia standardowego dla każdego składnika
Python3
typ w Javie
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Wyjście :

Epoka a logarytm wiarygodności
Narysuj ostateczną szacunkową gęstość
Python3
strony z filmami podobne do 123movies
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Wyjście :
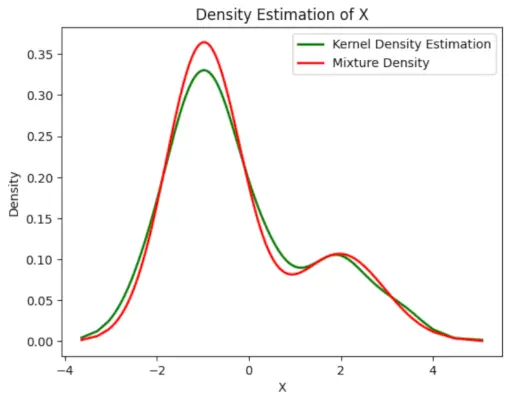
Szacowana gęstość
Zastosowania Algorytm EM
- Można go wykorzystać do uzupełnienia brakujących danych w próbce.
- Można go wykorzystać jako podstawę do nienadzorowanego uczenia się klastrów.
- Można go wykorzystać do estymacji parametrów Ukrytego Modelu Markowa (HMM).
- Można go wykorzystać do odkrywania wartości zmiennych ukrytych.
Zalety algorytmu EM
- Zawsze mamy gwarancję, że prawdopodobieństwo będzie rosło z każdą iteracją.
- Krok E i krok M są często dość łatwe w przypadku wielu problemów związanych z wdrażaniem.
- Rozwiązania M-kroków często istnieją w formie zamkniętej.
Wady algorytmu EM
- Charakteryzuje się powolną zbieżnością.
- Dokonuje zbieżności tylko do lokalnych optimów.
- Wymaga obu prawdopodobieństw, do przodu i do tyłu (optymalizacja numeryczna wymaga tylko prawdopodobieństwa do przodu).
