Prawo chłodzenia Newtona to podstawowe prawo opisujące szybkość przekazywania ciepła przez ciało do otoczenia poprzez promieniowanie. Prawo to stanowi, że szybkość, z jaką ciało emituje ciepło, jest wprost proporcjonalna do różnicy temperatur ciała od otoczenia, pod warunkiem, że różnica temperatur jest niewielka. tzn. im większa różnica pomiędzy temperaturą ciała i jego otoczenia, tym więcej ciepła jest tracone, a im niższa temperatura, tym mniej ciepła. Prawo chłodzenia Newtona jest szczególnym przypadkiem prawa Stefana-Boltzmanna.

W tym artykule dowiemy się szczegółowo o prawie chłodzenia Newtona, prawie chłodzenia Newtona, jego wyprowadzeniu, przykładach i innych szczegółach.

Definicja prawa chłodzenia Newtona

Niuton jako pierwszy zbadał związek między ciepłem oddanym przez ciało do otoczenia. Twierdzi, że im większa jest różnica temperatur pomiędzy przedmiotem a otoczeniem, tym więcej ciepła wypromieniowuje ciało.

Prawo chłodzenia Newtona stwierdza, że

Szybkość utraty ciepła z ciała jest wprost proporcjonalna do różnicy temperatur pomiędzy ciałem a jego otoczeniem, pod warunkiem, że różnica temperatur nie jest duża.

Prawo to służy do wyjaśnienia, dlaczego gorąca woda lub mleko pozostawione na stole ochładza się szybciej niż odrobina ciepłego mleka lub wody pozostawiona na stole. Prawo chłodzenia Newtona pomaga nam zmierzyć temperaturę dowolnej osoby bez jej mierzenia, biorąc pod uwagę początkową temperaturę ciała i temperaturę otoczenia.

Wzór na prawo chłodzenia Newtona

Wzór na prawo chłodzenia Newtona to wzór umożliwiający obliczenie temperatury materiału podczas oddawania ciepła do otoczenia w wyniku promieniowania.

Zgodnie z prawem chłodzenia Newtona,

Szybkość utraty ciepła ( – dQ/dt) ciała jest wprost proporcjonalna do różnicy temperatur [ΔT = (T ₂ - T ₁ )] ciała i otoczenia.

historia w Javie

Możemy to przedstawić jako,

– dQ/dt ∝ (T ₂ - T ₁ )

– dQ/dt = k(T ₂ - T ₁ )

Gdzie,
k jest stałą proporcjonalności

Rozwiązując powyższe równanie różniczkowe otrzymujemy,

T(t) = T _S + (T _O - T _S ) To jest ^-kt

Gdzie,
T to jest czas
T(t) jest temperaturą ciała w chwili t
T _S to temperatura otoczenia
T _O to początkowa temperatura ciała
k jest stałą proporcjonalności

Wyprowadzenie prawa chłodzenia Newtona

Wzór na prawo chłodzenia Newtona można wyprowadzić, korzystając z rozwiązania równania różniczkowego. Niech ciało o masie m i pojemności cieplnej właściwej s ma temperaturę T₂oraz T₁jest temperatura otoczenia.

Jeśli temperatura spadnie o niewielką ilość dT ₂ w samą porę dt , wówczas ilość ciepła utraconego wynosi,

dQ = ms dT ₂

Szybkość utraty ciepła jest wyrażona wzorem,

dQ/dt = ms (dT ₂ /dt)

Zgodnie z prawem chłodzenia Newtona,

– dQ/dt = k(T ₂ - T ₁ )

Porównując powyższe równanie

– ms (dT ₂ /dt) = k (T ₂ - T ₁ )

dT ₂ /(T ₂ -T ₁ ) = – (k/ms) dt

dT ₂ /(T ₂ - T ₁ ) = – Kdt

Gdzie, K = k/m s

Całkowanie powyższego równania

dziennik _{To jest} (T ₂ - T ₁ ) = – K. t + do

T ₂ = T ₁ + C’ i ^–Kt

Gdzie, C’ = e ^C

Zależność spadku temperatury ciała od czasu przedstawiono za pomocą wykresu chłodzenia. Nachylenie tego wykresu pokazuje szybkość spadku temperatury.

zamień całą Javę

Krzywa chłodzenia to wykres przedstawiający zależność między temperaturą ciała a czasem. Szybkość spadku temperatury zależy od nachylenia stycznej do krzywej w dowolnym punkcie. Obraz dodany poniżej pokazuje zależność spadku temperatury od czasu.

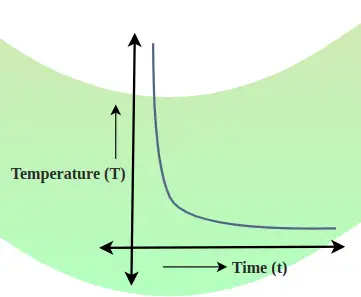
Ogólnie,

T(t) = T _A +(T _H -T _A )To jest ^-kt

Gdzie
T(t) jest temperaturą w chwili t
T _A to temperatura otoczenia lub temperatura otoczenia
T _H jest temperaturą gorącego obiektu
k jest stałą dodatnią, a t jest czasem

Metody stosowania prawa chłodzenia Newtona

Przy stałej szybkości chłodzenia, szybkość chłodzenia odnosi się do średniej temperatury ciała w danym przedziale, a następnie możemy obliczyć przybliżoną wartość, korzystając z prawa chłodzenia Newtona

dθ/dt = k(q – q _S )

Gdzie,
Q jest temperatura ciała
Q _S jest temperatura otoczenia

Teraz, jeśli średnia temperatura ciała wynosi q, gdzie:

q = (q _I + q _F )/2

Weryfikacja prawa chłodzenia Newtona

Możemy łatwo zweryfikować prawo chłodzenia Newtona za pomocą eksperymentu opisanego poniżej:

W eksperymencie bierzemy naczynie o podwójnych ściankach (V) z wodą pomiędzy ścianami. Wewnątrz naczynia o podwójnych ściankach pobieramy kalorymetr miedziany (C) zawierający gorącą wodę.

Używamy dwóch termometrów T₂do pomiaru temperatury wody w kalorymetrze i T₁do pomiaru temperatury gorącej wody pomiędzy podwójnymi ścianami. Po równych odstępach czasu odnotowuje się obie temperatury i tworzy wykres pomiędzy logami_{To jest}(T₂-T₁) i czas (t) są wykreślane w postaci linii prostej o nachyleniu ujemnym.

Wykres prawa chłodzenia Newtona

Poniżej dodano wykres prawa chłodzenia Newtona, na którym pokazano log różnicy pomiędzy dwiema temperaturami i czasem.

Ograniczenia prawa chłodzenia Newtona

Różne ograniczenia prawa chłodzenia Newtona to:

• Prawo chłodzenia Newtona obowiązuje, jeśli różnica temperatur między ciałem a otoczeniem jest niewielka.
• Strata ciepła przez organizm następuje wyłącznie w postaci: Promieniowanie .
• Temperatura otoczenia musi pozostać stała podczas chłodzenia ciała, w przeciwnym razie prawo chłodzenia Newtona nie jest prawdziwe.

Zastosowania prawa chłodzenia Newtona

Różne zastosowania prawa chłodzenia Newtona to:

• Aby oszacować, ile czasu zajmie ciepłemu obiektowi ochłodzenie się do określonej temperatury.
• Aby określić temperaturę napoju w lodówce po upływie określonego czasu.
• Pomaga określić czas śmierci, sprawdzając możliwą temperaturę ciała w chwili śmierci i aktualną temperaturę ciała.

Czytaj więcej,

ciąg zawiera Java

• Specyficzna pojemność cieplna
• Podstawowa koncepcja termodynamiki
• Procesy termodynamiczne

Rozwiązane przykłady Prawo chłodzenia Newtona

Przykład 1: Naczynie wypełnione gorącą potrawą schładza się z 94°C do 86°C w ciągu 2 minut, gdy temperatura w pomieszczeniu wynosi 20°C. Ile czasu zajmie ochłodzenie z 71°C do 69°C?

Rozwiązanie:

Średnia z 94°C i 86°C to 90°C,

• T₂= 90°C
• T₁= 20°C

Wrzuć tem. żywności wynosi 8°C w ciągu 2 minut.

Zgodnie z prawem chłodzenia Newtona,

– dQ/dt = k(T ₂ -T ₁ )

8°C /2 min = k(90 – 20)

4 = k(70) ………(1)

Średnia temperatura 69°C i 71°C wynosi 70°C

• T₂= 70°C
• T₁= 20°C

Zgodnie z prawem chłodzenia Newtona,

2°C /dt = k(70 – 20) ……(2)

Z równań (1) i (2)

Zmiana czasu = 0,7 min = =42 sek

W związku z tym schładzanie żywności z 71°C do 69°C zajmie 42 sekundy.

Przykład 2: Ciało o temperaturze 40°C przebywa się w otoczeniu o stałej temperaturze 20°C. Obserwuje się, że w ciągu 10 minut jego temperatura spada do 35°C. Oblicz, ile czasu zajmie ciału osiągnięcie temperatury 30°C.

Rozwiązanie:

Dany,

• Q_I= (40 – 20)°C
• Q_F= (35 – 20)°C

Zgodnie z prawem chłodzenia Newtona

Q _F = q _I To jest ^-kt

Teraz dla przedziału, w którym temperatura spada z 40°C do 35°C.

(35 – 20) = (40 – 20) i^{-(10 tys.)}

To jest^{-10 tys}= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Teraz ponownie korzystając ze wzoru Newona,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

To jest^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Korzystając z wartości k,

t = 0,40546/0,02876

t = 14,098 min

Zatem czas potrzebny organizmowi na osiągnięcie temperatury 30°C wynosi 14,098 min

Przykład 3: Olej podgrzewa się do 70°C. Po 6 minutach schładza się do 50°C. Oblicz czas potrzebny olejowi na ochłodzenie się z 50°C do 40°C, biorąc pod uwagę temperaturę otoczenia T _S = 25°C

Rozwiązanie:

Dany,

Temperatura oleju po 6 min tj. T(t) wynosi 50°C

zmienna typu Java

• Temperatura otoczenia T_S= 25°C
• Temperatura oleju, T_O= 70°C
• Czas schładzania do 50°C = 6 min

Zgodnie z prawem chłodzenia Newtona,

T(t) = T_S+ (T₀- T_S) To jest^-kt

{T(t) – T_S}/(T_O- T_S) = i^-kt

-kt = ln[(T(t) – T_S)/(T_O- T_S)] ………(1)

Zastąp wartości

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

Średnia temperatura od 50°C do 40°C wynosi 45°C

Ponownie skorzystaj z prawa chłodzenia Newtona

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Zatem czas schładzania oleju z 50°C do 40°C wynosi 8,278 min

Przykład 4: Wodę podgrzewa się do 80°C przez 10 minut. Jaka byłaby jego temperatura w stopniach Celsjusza, gdyby k = 0,056 na minutę, a temperatura otoczenia wynosiła 25°C?

Rozwiązanie:

Dany,

• Temperatura otoczenia T_S= 25°C
• Temperatura wody T₀= 80°C
• Czas podgrzewania wody (t) = 10 min
• Wartość stałej k = 0,056.

Zgodnie z prawem chłodzenia Newtona,

T(t) = T_S+ (T₀- T_S) To jest^-kt

Zastąpienie wartości

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55 e^-(0,056×10)

T(t) = 25 + 31,42

T(t) = 56,42

Po 10 minutach temperatura wody będzie wynosić 56,42°C.

Często zadawane pytania dotyczące prawa chłodzenia Newtona

P1: Jakie jest prawo chłodzenia Newtona?

Odpowiedź:

Prawo chłodzenia Newtona stwierdza, że ​​szybkość utraty ciepła przez ciało jest wprost proporcjonalna do różnicy temperatur pomiędzy ciałem a jego otoczeniem.

P2: Jaki jest wzór na prawo chłodzenia Newtona?

Odpowiedź:

Wzór na prawo chłodzenia Newtona stwierdza, że:

T(t) = T _S + (T _O - T _S ) To jest ^-kt

poradnik dotyczący selenu

P3: Ile wynosi k w prawie chłodzenia Newtona?

Odpowiedź:

The k we wzorze „Prawo chłodzenia Newtona” jest stałą zależną od materiału, tj. zmiana materiału powoduje zmianę k w prawie chłodzenia Newtona.

P4: Dlaczego gorące mleko łatwiej jest pić z miski niż ze szklanki?

Odpowiedź:

Miska ma większą powierzchnię niż szkło, dlatego też więcej ciepła oddaje do otoczenia w postaci promieniowania cieplnego przez miskę, dzięki czemu łatwiej jest nam pić z niej gorące mleko.