CO TO JEST NAchylenie?

Liczba wartości bezwzględnych, które określają, czy linia jest bardziej strome lub płaskie i kierunek linii na wykresie są znane jako a nachylenie lub nachylenie. Nachylenie linii jest podstawowym pojęciem w ekonomii i matematyce. Zwykle jest to oznaczone literą 'M'. Nachylenie można obliczyć, dzieląc „zmiana pionowa” z „zmiana pozioma” pomiędzy dwoma różnymi punktami na linii.

RODZAJE STOKU

Istnieją dwa główne typy zboczy, które podano poniżej:

Nachylenie dodatnie:Nachylenie, w którym dwie zmienne, tj. zmienna na osi x i zmienna na osi y, pokazują pozytywna relacja jest znany jako nachylenie dodatnie. Mówiąc prościej, nachylenie dodatnie to takie, w którym zmienna x rośnie wraz ze wzrostem zmiennej y i/lub zmienna y rośnie wraz ze wzrostem zmiennej x. Podobnie zmienna x maleje wraz ze spadkiem zmiennej y i/lub zmienna y maleje wraz ze spadkiem zmiennej x. Oznacza to, że obie zmienne są uzupełnia do siebie. Dodatnie nachylenie przesuwa się w kierunek w górę lub jest nachylony ku górze.
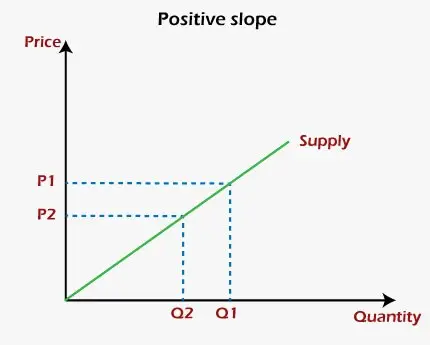
W ujęciu graficznym nachylenie dodatnie to takie, w którym linia na wykresie rośnie, gdy przesuwa się od lewej do prawej. Pojęcie dodatniego nachylenia można łatwo zrozumieć za pomocą krzywa podaży producenta lub firmy w ekonomii. Dwie zmienne krzywej to cena na osi y i ilość towarów na osi x. Załóżmy, że firma produkuje towary dla maksymalizacja zysków. Dlatego też, gdy ceny towarów wzrosną, ilość dostarczana przez firmę również wzrośnie, natomiast gdy ceny spadną, ilość dostarczana przez firmę zmniejszy się. Innymi słowy, przy wyższych cenach firma lub producent zwiększy dostarczaną ilość, aby uzyskać większy zysk, natomiast przy niższych cenach zmniejszy dostarczaną ilość, aby zmniejszyć straty. Pokazuje zatem, że ceny i dostarczana ilość są ze sobą dodatnio powiązane, co można wyczytać z poniższego diagramu:
Nachylenie ujemne:Nachylenie, w którym dwie zmienne, tj. zmienna na osi x i zmienna na osi y, pokazują negatywna relacja jest znany jako nachylenie ujemne. Innymi słowy, nachylenie ujemne to takie, w którym zmienna x rośnie wraz ze spadkiem zmiennej y i/lub zmienna y rośnie wraz ze spadkiem zmiennej x. W ten sam sposób zmienna x maleje wraz ze wzrostem zmiennej y i/lub zmienna y maleje wraz ze wzrostem zmiennej x. To reprezentuje odwrotna relacja pomiędzy tymi dwiema zmiennymi. Nachylenie ujemne przesuwa się w kierunek w dół lub jest opadająca.
Graficznie, nachylenie ujemne to takie, w którym linia na wykresie opada, gdy przesuwa się od lewej do prawej. Jednym z najlepszych przykładów ujemnego nachylenia wykresu jest: krzywa popytu w ekonomii. Dwie zmienne krzywej to cena na osi y i ilość towarów na osi x. Jak wiemy, konsumenci kupują większą ilość dobra po cenie niższej niż po cenie wyższej. Zatem wraz ze wzrostem cen tych dóbr wielkość popytu ze strony konsumentów na towary będzie się zmniejszać. Z drugiej strony, gdy ceny towarów spadną, popyt ilościowy wzrośnie. Stąd wynika A negatywna relacja pomiędzy cenami a ilością dostarczonych towarów. Można to wyczytać ze schematu podanego poniżej:

DWA INNE TYPY STOKU

Oprócz nachyleń dodatnich i ujemnych istnieją jeszcze dwa typy nachyleń, zwane nachyleniem zerowym i nachyleniem nieskończonym. Można je zrozumieć na podstawie podanego wyjaśnienia:

Nachylenie zerowe:Stan, w którym zmienna na osi y pozostaje taka sama wraz ze zmianą zmiennej na osi x, nazywa się nachylenie zera. Graficznie, A linia pozioma lub płaska na wykresie ma zerowe nachylenie. Dlatego nazywa się to A stała funkcja. Nachylenie zerowe nie przesuwa się ani w górę, ani w dół. Porusza się tylko w lewo lub w prawo.
Diagram podany poniżej jest graficzną prezentacją nachylenia zerowego:
Nieskończone nachylenie:Stan, w którym zmienna na osi x pozostaje taka sama wraz ze zmianą zmiennej na osi y, nazywa się nieskończone nachylenie. Nazywa się to również nieokreślone nachylenie. Zgodnie z warunkami graficznymi, a linia pionowa lub prostopadła na wykresie ma nieskończone nachylenie. Nieskończone nachylenie nie przesuwa się ani w lewo, ani w prawo. Pokazuje ruch tylko w górę lub w dół.
Na podanym schemacie pokazano nieskończone nachylenie:

OBLICZANIE NACHYLENIA

• W równaniu liniowym topór + o + c = 0, nachylenie definiuje się jako -a/b.
• Równanie prostej można obliczyć za pomocą wzoru wzór na nachylenie punktu jeśli oba nachylenie M linii i punktu (x1, y1) są znane. Wzór podano poniżej:
  y - y1 = m (x - x1)
• Będzie dwuliniowy równoległy jeśli ich zbocza są równy, podczas gdy dwie linie będą prostopadły jeśli iloczyn ich nachyleń wynosi -1.

DODATKOWE INFORMACJE

• Wartość bezwzględna nachylenia służy do sprawdzenia, czy krzywa jest bardziej strome lub płaskie.
• Dodatnia i ujemna wartość nachylenia decyduje o kierunku, tj. w górę lub w dół, ze zbocza.
• Krzywa staje się bardziej stromo wraz ze wzrostem wartości bezwzględnej nachylenia.
• Krzywa staje się pochlebiało wraz ze spadkiem wartości bezwzględnej nachylenia.
• Na te warunki nie ma wpływu nachylenie ujemne lub dodatnie (nie wartość ujemna lub dodatnia).
• A niższe nachylenie dodatnie oznacza, że ​​utworzona zostanie bardziej płaska krzywa nachylona w górę.
• A wyższe nachylenie dodatnie oznacza, że ​​utworzona zostanie bardziej stroma krzywa wygięta w górę.
• A nachylenie ujemne o dużej wartości bezwzględnej oznacza, że ​​utworzy się bardziej stroma krzywa nachylona w dół.
• A nachylenie ujemne o mniejszej wartości bezwzględnej oznacza, że ​​utworzona zostanie bardziej płaska krzywa wygięta w dół.