W tym artykule omówimy przechodzenie postordera w strukturze danych.
Liniowe struktury danych, takie jak stos, tablica, kolejka itp., mają tylko jeden sposób przeglądania danych. Ale w hierarchicznej strukturze danych, takiej jak drzewo istnieje wiele sposobów przeglądania danych. Zatem tutaj omówimy inny sposób poruszania się po drzewiastej strukturze danych, tj. przechodzenie przez pocztę . Przechodzenie postorderowe jest jedną z technik przechodzenia używanych do odwiedzania węzła w drzewie. Kieruje się zasadą LRN (węzeł lewy-prawy) . Przechodzenie postorderowe służy do uzyskania wyrażenia postfiksowego drzewa.
Do wykonania przejścia po zamówieniu wykorzystywane są następujące kroki:
- Przejdź przez lewe poddrzewo, wywołując rekursywnie funkcję postorder.
- Przejdź przez prawe poddrzewo, wywołując rekursywnie funkcję postorder.
- Uzyskaj dostęp do części danych bieżącego węzła.
Technika przechodzenia po zamówieniu jest zgodna z Lewy prawy korzeń polityka. W tym przypadku lewy prawy korzeń oznacza, że najpierw przemierzane jest lewe poddrzewo węzła głównego, następnie prawe poddrzewo, a na końcu przechodzi węzeł główny. W tym przypadku sama nazwa Postorder sugeruje, że węzeł główny drzewa zostanie w końcu przebyty.
Algorytm
Przyjrzyjmy się teraz algorytmowi przechodzenia postordera.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: POSTORDER(TREE -> LEFT) Step 3: POSTORDER(TREE -> RIGHT) Step 4: Write TREE -> DATA [END OF LOOP] Step 5: END
Przykład przejścia sprzedaży wysyłkowej
Zobaczmy teraz przykład przechodzenia po zamówieniu. Proces postorder traversal łatwiej będzie zrozumieć na przykładzie.
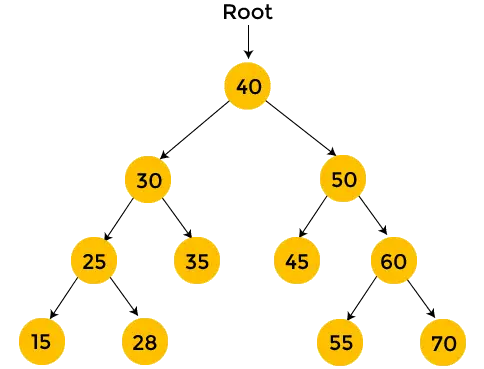
Węzły oznaczone żółtym kolorem nie zostały jeszcze odwiedzone. Teraz będziemy przechodzić przez węzły powyższego drzewa, korzystając z przechodzenia postorderowego.
- Tutaj 40 to węzeł główny. Najpierw odwiedzamy lewe poddrzewo liczby 40, tj. 30. Węzeł 30 również będzie przechodził w kolejności pocztowej. 25 to lewe poddrzewo liczby 30, zatem jest ono również przeglądane w kolejności pocztowej. Zatem 15 jest lewym poddrzewem liczby 25. Ale 15 nie ma poddrzewa, więc wydrukować 15 i przejdź w kierunku prawego poddrzewa liczby 25.
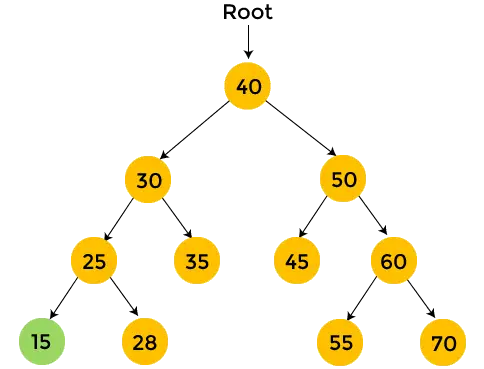
- 28 jest prawym poddrzewem liczby 25 i nie ma dzieci. Więc, wydrukować 28 .
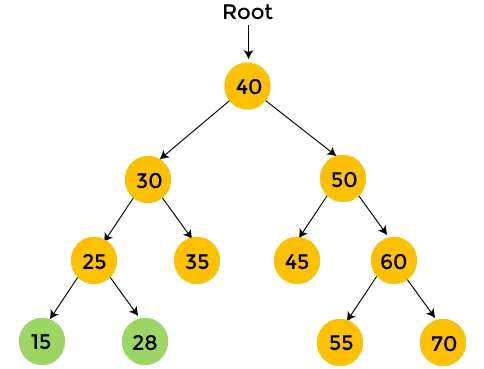
- Teraz, wydrukować 25 i przechodzenie po zamówieniu dla 25 skończone.
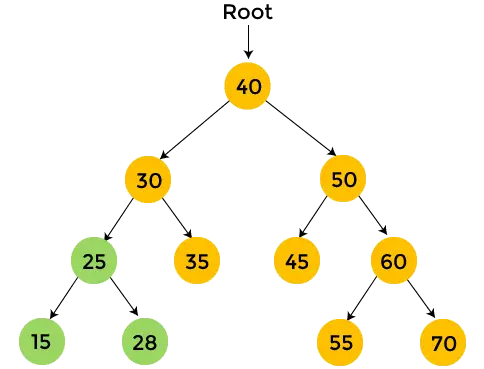
- Następnie przejdź w kierunku prawego poddrzewa liczby 30. 35 jest prawym poddrzewem liczby 30 i nie ma dzieci. Więc, wydrukować 35 .
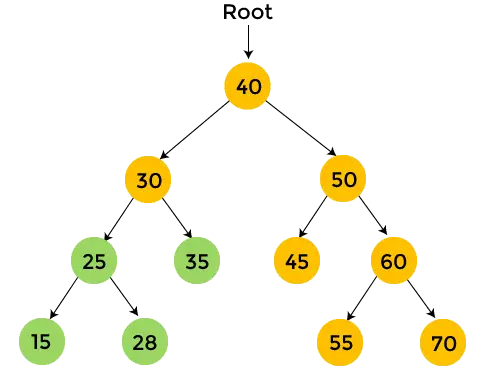
- Po tym, wydrukować 30 i przechodzenie po zamówieniu dla 30 skończone. Zatem przechodzi się przez lewe poddrzewo danego drzewa binarnego.
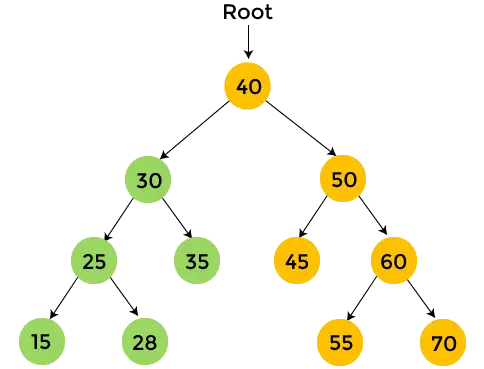
- Teraz przejdź w kierunku prawego poddrzewa liczby 40, czyli 50, i ono również będzie przechodzić w kolejności pocztowej. 45 jest lewym poddrzewem liczby 50 i nie ma dzieci. Więc, wydrukować 45 i przejdź w kierunku prawego poddrzewa liczby 50.
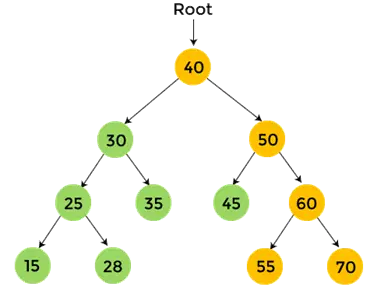
- 60 to prawe poddrzewo liczby 50, które będzie również przeglądane w kolejności pocztowej. 55 to lewe poddrzewo liczby 60, które nie ma dzieci. Więc, wydrukować 55 .
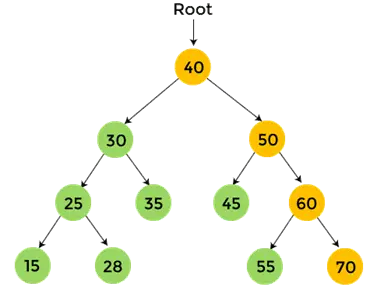
- Teraz, wydrukować 70, które jest prawym poddrzewem liczby 60.
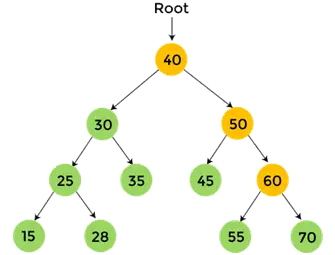
- Teraz, drukuj 60, i przechodzenie po złożeniu zamówienia na 60 zostało zakończone.
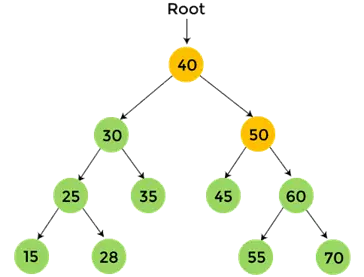
- Teraz, wydrukuj 50, i przechodzenie po złożeniu zamówienia na 50 zostało zakończone.
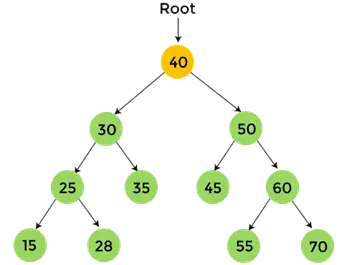
- W końcu, drukuj 40, który jest węzłem głównym danego drzewa binarnego i przechodzenie po kolejności dla węzła 40 zostało zakończone.
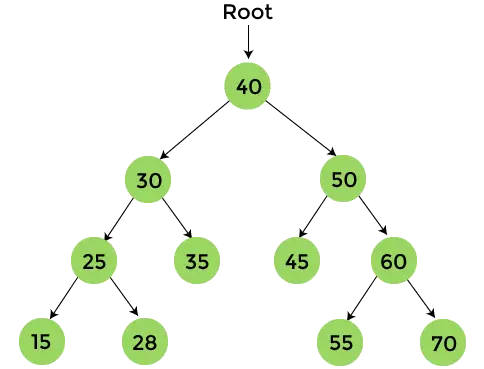
Ostateczny wynik, który otrzymamy po przejściu postordera to -
{15, 28, 25, 35, 30, 45, 55, 70, 60, 50, 40}
Złożoność ruchu wysyłkowego
Złożoność czasowa przejścia postordera wynosi NA) , gdzie „n” jest rozmiarem drzewa binarnego.
Natomiast złożoność przestrzenna przemieszczania się po zamówieniu wynosi O(1) , jeśli nie weźmiemy pod uwagę rozmiaru stosu dla wywołań funkcji. W przeciwnym razie złożoność przestrzenna przemieszczania się po zamówieniu wynosi Oh) , gdzie „h” jest wysokością drzewa.
Implementacja obsługi zamówień pocztowych
Przyjrzyjmy się teraz implementacji postorder traversal w różnych językach programowania.
Program: Napisz program realizujący realizację postorder travers w języku C.
#include #include struct node { s struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Wyjście

Program: Napisz program implementujący przechodzenie postordera w języku C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the postorder traversal of given binary tree is -
'; traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-14.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-15.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-16.webp" alt="Postorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -

Program: Napisz program implementujący przechodzenie postordera w Javie.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -

To tyle na temat artykułu. Mam nadzieję, że artykuł będzie dla Ciebie pomocny i pouczający.











