W tym artykule omówimy przechodzenie przedpremierowe w strukturze danych. Liniowe struktury danych, takie jak stos, tablica, kolejka itp., mają tylko jeden sposób przeglądania danych. Ale w hierarchicznej strukturze danych, takiej jak drzewo istnieje wiele sposobów przeglądania danych.
W przypadku przeglądania w przedsprzedaży najpierw odwiedzany jest węzeł główny, następnie lewe poddrzewo, a następnie prawe poddrzewo. Proces przeglądania zamówień w przedsprzedaży można przedstawić jako -
wycinek tablicy Java
root → left → right
Węzeł główny jest zawsze przemierzany jako pierwszy w przypadku przechodzenia w przedsprzedaży, podczas gdy jest to ostatni element w przypadku przechodzenia po zamówieniu. Przechodzenie w przedsprzedaży służy do uzyskania wyrażenia przedrostka drzewa.
Czynności wymagane do wykonania zamówienia w przedsprzedaży są następujące:
- Najpierw odwiedź węzeł główny.
- Następnie odwiedź lewe poddrzewo.
- Na koniec odwiedź prawe poddrzewo.
Technika przeglądania zamówień w przedsprzedaży jest zgodna z Korzeń Lewy Prawy polityka. Już sama nazwa preorder sugeruje, że węzeł główny zostanie przebyty jako pierwszy.
Algorytm
Przyjrzyjmy się teraz algorytmowi przemierzania zamówień w przedsprzedaży.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: Write TREE -> DATA Step 3: PREORDER(TREE -> LEFT) Step 4: PREORDER(TREE -> RIGHT) [END OF LOOP] Step 5: END
Przykład przejścia zamówienia w przedsprzedaży
Zobaczmy teraz przykład przeglądania zamówień w przedsprzedaży. Proces przeglądania przedsprzedaży łatwiej będzie zrozumieć na przykładzie.
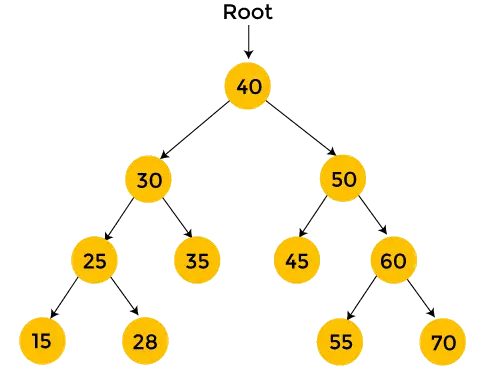
Węzły oznaczone żółtym kolorem nie zostały jeszcze odwiedzone. Teraz będziemy przechodzić przez węzły powyższego drzewa, korzystając z przechodzenia w przedsprzedaży.
- Zacznij od węzła głównego 40. Najpierw wydrukować 40 a następnie rekurencyjnie przechodź przez lewe poddrzewo.
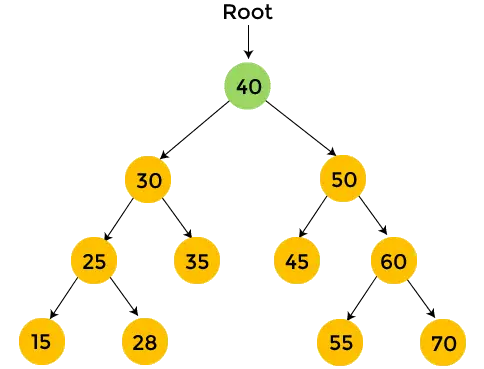
- Teraz przejdź do lewego poddrzewa. W przypadku lewego poddrzewa węzeł główny to 30. Drukuj 30 i przejdź w kierunku lewego poddrzewa liczby 30.
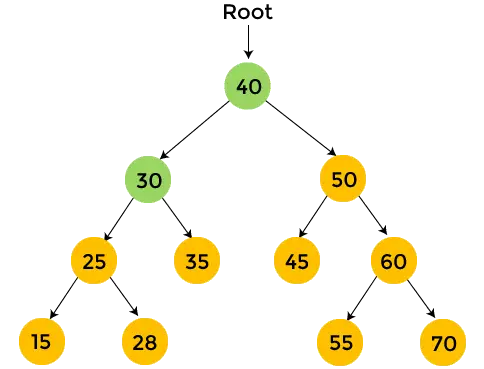
- W lewym poddrzewie liczby 30 znajduje się element 25, czyli wydrukować 25 i przemierzamy lewe poddrzewo liczby 25.
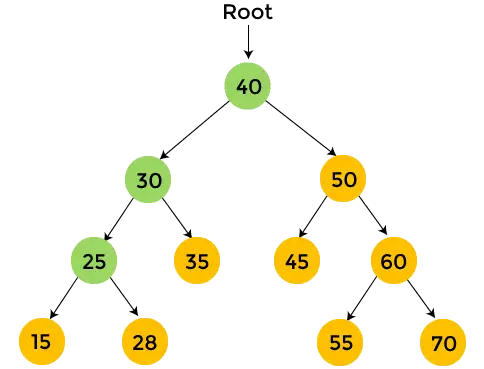
- W lewym poddrzewie liczby 25 znajduje się element 15, a 15 nie ma poddrzewa. Więc, wydrukować 15 i przejdź do prawego poddrzewa liczby 25.
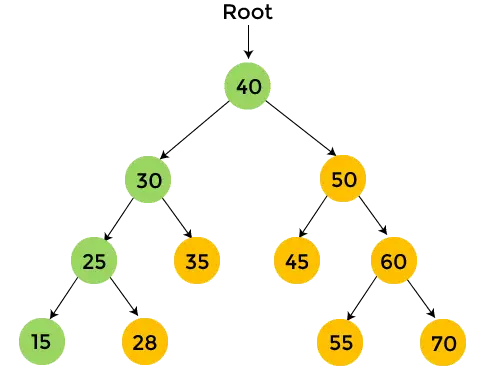
- W prawym poddrzewie liczby 25 znajduje się 28, a 28 nie ma poddrzewa. Więc, wydrukować 28 i przejdź do prawego poddrzewa liczby 30.
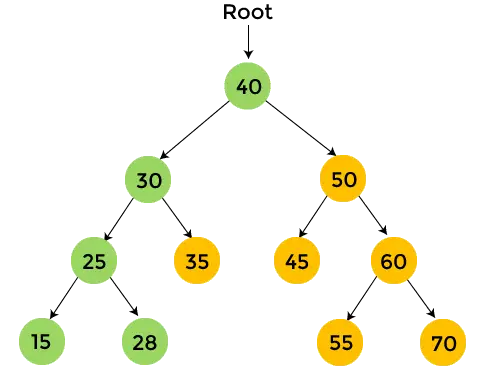
- W prawym poddrzewie liczby 30 znajduje się 35, które nie ma poddrzewa. Więc wydrukować 35 i przechodzimy przez prawe poddrzewo liczby 40.
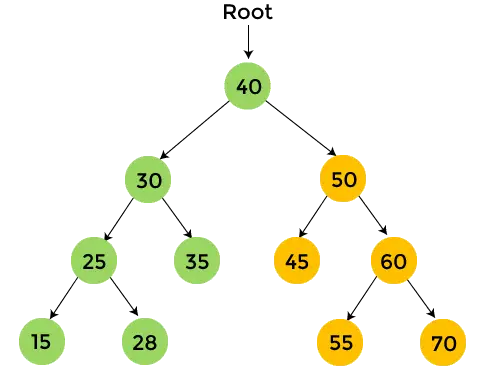
- W prawym poddrzewie liczby 40 znajduje się liczba 50. Wydrukuj 50 i przejdź przez lewe poddrzewo liczby 50.
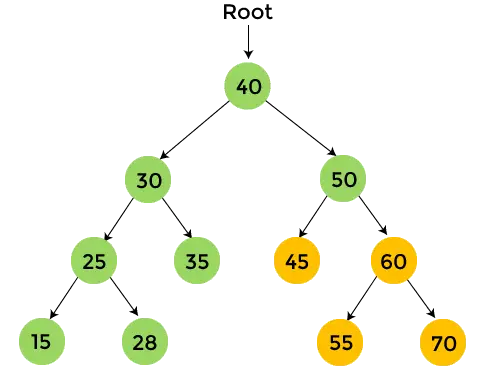
- W lewym poddrzewie liczby 50 znajduje się 45, które nie mają dzieci. Więc, wydrukować 45 i przejdź przez prawe poddrzewo liczby 50.
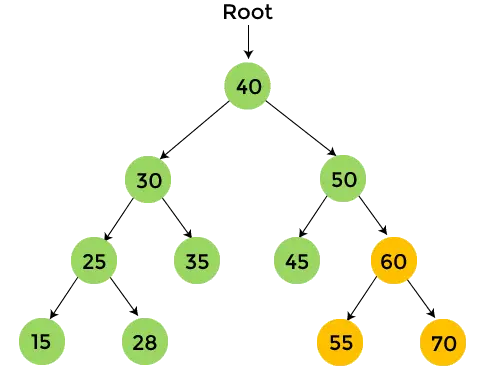
- W prawym poddrzewie liczby 50 znajduje się 60. Drukuj 60 i przemierzamy lewe poddrzewo liczby 60.
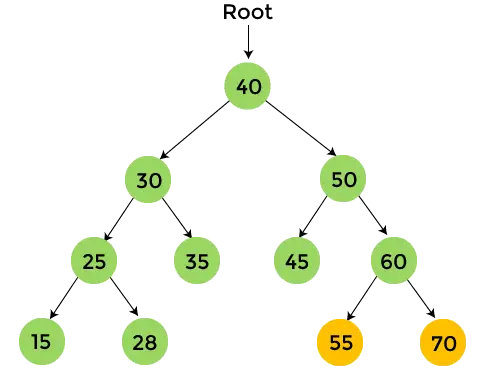
- W lewym poddrzewie liczby 60 znajduje się liczba 55, która nie ma żadnego dziecka. Więc, wydrukować 55 i przejdź do prawego poddrzewa liczby 60.
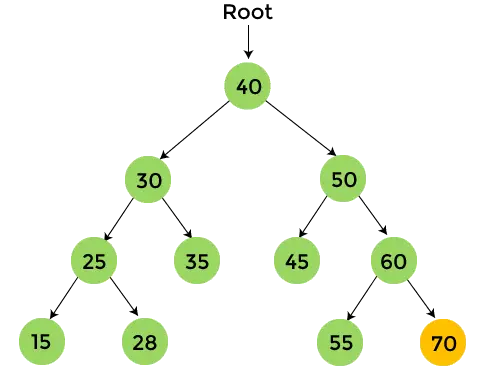
- W prawym poddrzewie liczby 60 znajduje się 70, które nie mają żadnego dziecka. Więc, wydrukować 70 i zatrzymać proces.
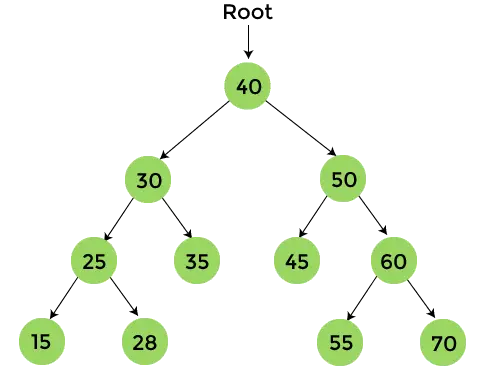
Po zakończeniu przeglądania zamówień w przedsprzedaży ostateczny wynik to -
40, 30, 25, 15, 28, 35, 50, 45, 60, 55, 70
Złożoność przeglądania zamówień w przedsprzedaży
Złożoność czasowa przejścia zamówienia w przedsprzedaży wynosi NA) , gdzie „n” jest rozmiarem drzewa binarnego.
Natomiast złożoność przestrzenna podróży w przedsprzedaży wynosi O(1) , jeśli nie weźmiemy pod uwagę rozmiaru stosu dla wywołań funkcji. W przeciwnym razie złożoność przestrzenna podróży w przedsprzedaży wynosi Oh) , gdzie „h” jest wysokością drzewa.
Implementacja przejścia przedsprzedażowego
Przyjrzyjmy się teraz implementacji przeglądania zamówień w przedsprzedaży w różnych językach programowania.
Program: Napisz program realizujący przeglądanie zamówień przedpremierowych w języku C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); return 0; } Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -

Program: Napisz program implementujący przechodzenie przedpremierowe w języku C++.
hashset vs hashmap
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } int main() { struct node* root = createNode(39); root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-14.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(38); bt.root.left = new Node(28); bt.root.right = new Node(48); bt.root.left.left = new Node(23); bt.root.left.right = new Node(33); bt.root.left.left.left = new Node(13); bt.root.left.left.right = new Node(26); bt.root.right.left = new Node(43); bt.root.right.right = new Node(58); bt.root.right.right.left = new Node(53); bt.root.right.right.right = new Node(68); Console.WriteLine('Preorder traversal of given binary tree is - '); bt.traversePreorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-15.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-16.webp" alt="Preorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -

Program: Napisz program implementujący przeglądanie zamówień przedpremierowych w Javie.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -

To tyle na temat artykułu. Mam nadzieję, że artykuł będzie dla Ciebie pomocny i pouczający.











