Funkcję rekurencyjną można zdefiniować jako procedurę, która wywołuje samą siebie bezpośrednio lub pośrednio.
Innymi słowy, funkcja rekurencyjna to funkcja, która rozwiązuje problem, rozwiązując mniejsze wystąpienia tego samego problemu. Technika ta jest powszechnie stosowana w programowaniu do rozwiązywania problemów, które można podzielić na prostsze, podobne podproblemy.
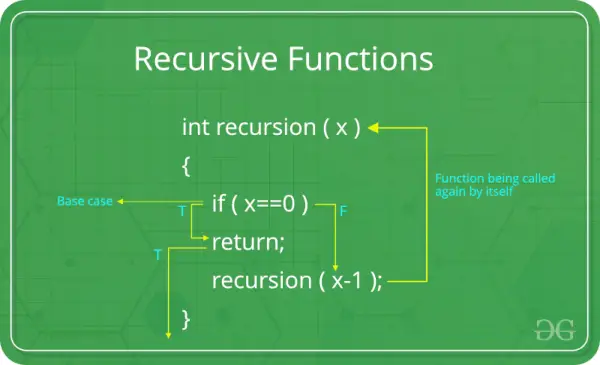
Potrzeba funkcji rekurencyjnej:
Funkcja rekurencyjna to funkcja, która rozwiązuje problem poprzez rozwiązywanie mniejszych wystąpień tego samego problemu. Technika ta jest często używana w programowaniu do rozwiązywania problemów, które można podzielić na prostsze, podobne podproblemy.
komentarze w Javie
1. Rozwiązywanie złożonych zadań:
Funkcje rekurencyjne dzielą złożone problemy na mniejsze wystąpienia tego samego problemu, co daje zwarty i czytelny kod.
2. Dziel i zwyciężaj:
Funkcje rekurencyjne nadają się do algorytmów dziel i zwyciężaj, takich jak sortowanie przez scalanie i szybkie sortowanie, dzielenie problemów na mniejsze podproblemy, rozwiązywanie ich rekurencyjnie i łączenie rozwiązań z pierwotnym problemem.
3. Cofanie się :
Rekursywne cofanie jest idealne do odkrywania i rozwiązywania problemów takich jak N-Queens i Sudoku.
4. Dynamiczny programowanie:
Funkcje rekurencyjne skutecznie rozwiązują problemy programowania dynamicznego, rozwiązując podproblemy i łącząc ich rozwiązania w kompletne rozwiązanie.
5. Drzewo i struktury grafów:
Funkcje rekurencyjne doskonale nadają się do pracy ze strukturami drzew i wykresów, upraszczając zadania związane z przechodzeniem i rozpoznawaniem wzorców .
Jak napisać funkcję rekurencyjną:
Składniki funkcji rekurencyjnej:
Obudowa podstawowa: Każda funkcja rekurencyjna musi mieć przypadek bazowy. Przypadek podstawowy to najprostszy scenariusz, który nie wymaga dalszej rekurencji. Jest to warunek zakończenia, który zapobiega wywoływaniu się funkcji przez czas nieokreślony. Bez odpowiedniego przypadku podstawowego funkcja rekurencyjna może prowadzić do nieskończonej rekurencji.
wykres alokacji zasobów
Przypadek rekurencyjny: W przypadku rekurencyjnym funkcja wywołuje samą siebie ze zmodyfikowanymi argumentami. Na tym polega istota rekurencji – rozwiązywanie większego problemu poprzez podzielenie go na mniejsze wystąpienia tego samego problemu. Przypadek rekurencyjny powinien z każdą iteracją zbliżać się do przypadku podstawowego.
Rozważmy przykład silnia liczby :
W tym przykładzie podstawowym przypadkiem jest kiedy N Jest 0 , a funkcja zwraca 1 . Przypadek rekurencyjny mnoży się N z wynikiem funkcji wywołanej z parametrem n – 1 . Proces trwa aż do osiągnięcia przypadku podstawowego.
Ważne jest, aby upewnić się, że funkcja rekurencyjna ma poprawny przypadek bazowy i że wywołania rekurencyjne prowadzą do przypadku bazowego, w przeciwnym razie procedura może działać w nieskończoność, co doprowadzi do przepełnienia stosu (przekroczenia dostępnej pamięci przydzielonej na wywołania funkcji).
Poniżej znajduje się implementacja silni liczby:
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> Jawa import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> Pyton # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> JavaScript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> Wyjście
Factorial of 4 is:24>
Złożoność czasowa: NA)
Przestrzeń pomocnicza: NA)
