W poniższym przykładzie istnieje sześć procesów o nazwach P1, P2, P3, P4, P5 i P6. Ich czas przybycia i czas wybuchu podano poniżej w tabeli. Kwant czasu układu wynosi 4 jednostki.
| Identyfikator procesu | Czas przybycia | Czas wybuchu |
|---|---|---|
| 1 | 0 | 5 |
| 2 | 1 | 6 |
| 3 | 2 | 3 |
| 4 | 3 | 1 |
| 5 | 4 | 5 |
| 6 | 6 | 4 |
Zgodnie z algorytmem musimy zachować gotową kolejkę i wykres Gantta. Struktura obu struktur danych zostanie zmieniona po każdym harmonogramie.
Gotowa kolejka:
Początkowo w czasie 0 przybywa proces P1, który zostanie zaplanowany na przedział czasu 4 jednostki. Zatem w kolejce gotowości będzie na początku tylko jeden proces P1 z czasem impulsu procesora wynoszącym 5 jednostek.
| P1 |
| 5 |
Wykres Gantta
Najpierw zostanie wykonany P1 dla 4 jednostek.
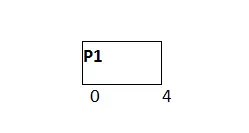
Gotowa kolejka
W międzyczasie wykonanie P1, cztery kolejne procesy P2, P3, P4 i P5 trafiają do kolejki gotowych. P1 nie został jeszcze ukończony, potrzebuje jeszcze 1 jednostki czasu, dlatego też zostanie dodany z powrotem do kolejki gotowych.
| P2 | P3 | P4 | P5 | P1 |
| 6 | 3 | 1 | 5 | 1 |
Wykres Gantta
Po P1, P2 będzie wykonywane przez 4 jednostki czasu, co pokazano na wykresie Gantta.

Gotowa kolejka
Podczas wykonywania P2 w kolejce gotowości pojawia się jeszcze jeden proces P6. Ponieważ P2 jeszcze się nie zakończył, P2 również zostanie dodany z powrotem do kolejki gotowości z pozostałym czasem serii wynoszącym 2 jednostki.
| P3 | P4 | P5 | P1 | P6 | P2 |
| 3 | 1 | 5 | 1 | 4 | 2 |
Wykres Gantta
Po P1 i P2, P3 będzie wykonywane przez 3 jednostki czasu, ponieważ czas jego działania procesora wynosi tylko 3 sekundy.

Gotowa kolejka
Ponieważ P3 został ukończony, zatem zostanie zakończony i nie zostanie dodany do kolejki gotowych. Następnym procesem, który zostanie wykonany, jest P4.
| P4 | P5 | P1 | P6 | P2 |
| 1 | 5 | 1 | 4 | 2 |
Wykres Gantta
Następnie zostaną wykonane P1, P2 i P3, P4. Jego czas wybuchu wynosi tylko 1 jednostkę, czyli jest mniejszy niż kwant czasu, dlatego zostanie ukończony.

Gotowa kolejka
Następnym procesem w kolejce gotowości jest P5 z 5 jednostkami czasu impulsu. Ponieważ P4 został ukończony, nie zostanie ponownie dodany do kolejki.
| P5 | P1 | P6 | P2 |
| 5 | 1 | 4 | 2 |
Wykres Gantta
P5 zostanie wykonane dla całego przedziału czasu, ponieważ wymaga 5 jednostek czasu impulsu, który jest dłuższy niż przedział czasu.

Gotowa kolejka
P5 nie został jeszcze ukończony; zostanie dodany z powrotem do kolejki z pozostałym czasem serii wynoszącym 1 jednostkę.
| P1 | P6 | P2 | P5 |
| 1 | 4 | 2 | 1 |
Wykres Gantta
Proces P1 otrzyma następną turę, aby zakończyć swoje wykonanie. Ponieważ wymaga tylko 1 jednostki czasu wybuchu, dlatego zostanie ukończony.

Gotowa kolejka
P1 jest ukończony i nie zostanie ponownie dodany do kolejki gotowych. Następny proces P6 wymaga tylko 4 jednostek czasu impulsu i zostanie wykonany jako następny.
| P6 | P2 | P5 |
| 4 | 2 | 1 |
Wykres Gantta
P6 będzie wykonywane przez 4 jednostki czasu do zakończenia.

Gotowa kolejka
Ponieważ P6 jest już ukończone, tym samym nie zostanie ponownie dodane do kolejki. W kolejce procesów gotowych znajdują się tylko dwa procesy. Następny proces P2 wymaga tylko 2 jednostek czasu.
| P2 | P5 |
| 2 | 1 |
Wykres Gantta
P2 zostanie wykonane ponownie, ponieważ wymaga tylko 2 jednostek czasu, dlatego zostanie ukończone.

Gotowa kolejka
Teraz jedynym dostępnym procesem w kolejce jest P5, który wymaga 1 jednostki czasu serii. Ponieważ przedział czasu składa się z 4 jednostek, zostanie on ukończony w następnej serii.
| P5 |
| 1 |
Wykres Gantta
P5 będzie wykonywane aż do zakończenia.

Czas realizacji, czas realizacji i czas oczekiwania zostaną obliczone zgodnie z poniższą tabelą.
Jak wiemy,
Turn Around Time = Completion Time - Arrival Time Waiting Time = Turn Around Time - Burst Time
| Identyfikator procesu | Czas przybycia | Czas wybuchu | Czas realizacji | Czas zawrócenia | Czas oczekiwania |
|---|---|---|---|---|---|
| 1 | 0 | 5 | 17 | 17 | 12 |
| 2 | 1 | 6 | 23 | 22 | 16 |
| 3 | 2 | 3 | jedenaście | 9 | 6 |
| 4 | 3 | 1 | 12 | 9 | 8 |
| 5 | 4 | 5 | 24 | 20 | piętnaście |
| 6 | 6 | 4 | dwadzieścia jeden | piętnaście | jedenaście |
Średni czas oczekiwania = (12+16+6+8+15+11)/6 = 76/6 jednostek
