Wzór na nachylenie służy do określenia stromości lub nachylenia linii. Współrzędne x i y punktów leżących na linii służą do obliczenia nachylenia linii. Zmiana współrzędnej y związana ze zmianą współrzędnej x nazywana jest nachyleniem linii i jest zwykle oznaczana literą m.

Spis treści

• Co to jest wzór na nachylenie?
• Formuła nachylenia
• Wyprowadzenie wzoru nachylenia
• Wzór na nachylenie linii (prostej).
• Równanie nachylenia
• Przykład dotyczący wzoru na nachylenie

Co to jest wzór na nachylenie?

Do obliczenia nachylenia linii potrzebny jest wzór na nachylenie. Do obliczenia nachylenia linii wymagane są współrzędne x i y punktów na linii. Stosunek zmiany współrzędnych y do zmiany współrzędnych x nazywa się nachyleniem linii.

Nachylenie (m) = zmiana y/zmiana x = Δy/Δx

Formuła nachylenia

W matematyce nachylenie linii służy do określenia stopnia nachylenia linii, tj. stromości linii. Aby określić nachylenie linii, potrzebujemy współrzędnych x i y punktów leżących na linii. Wzór na nachylenie to zmiana netto współrzędnej y podzielona przez zmianę netto współrzędnej x. Δy to zmiana współrzędnych y, a Δx to zmiana współrzędnych x. Stąd stosunek zmiany współrzędnych y do zmiany współrzędnych x jest określony wzorem:

Nachylenie (m) = zmiana y/zmiana x = Δy/Δx

m= (i ₂ - I ₁ )/(X ₂ - X ₁ )

Gdzie

• X₁i x₂są współrzędnymi osi X
• I₁i y₂są współrzędnymi osi Y

Wyprowadzenie wzoru nachylenia

Współrzędne x i y linii służą do obliczenia nachylenia linii. Zmiana netto współrzędnej y wynosi Δy, podczas gdy zmiana netto współrzędnej x wynosi Δx. Zatem zmianę współrzędnej y w odniesieniu do zmiany współrzędnej x można zapisać jako:

m = Δy/Δx

Gdzie,

• M jest nachylenie
• Δy jest zmianą współrzędnych y
• Δx jest zmianą współrzędnych x

Wiemy, że tg θ jest także nachyleniem linii, gdzie θ jest kątem utworzonym przez prostą z dodatnim kierunkiem osi x.

I, tan θ = wysokość/podstawa

Ponieważ wysokość/podstawa pomiędzy dowolnymi dwoma danymi punktami = (y₂- I₁)/(X₂- X₁)

Zatem równanie nachylenia wygląda następująco: m = tan θ = Δy/Δx

Z wykresu obserwujemy:

jak wyłączyć tryb programisty

Δy = (y₂- I₁)

Δx = (x₂- X₁)

Następnie wzór na nachylenie podaje się jako:

Nachylenie = m = (y ₂ - I ₁ )/(X ₂ - X ₁ )

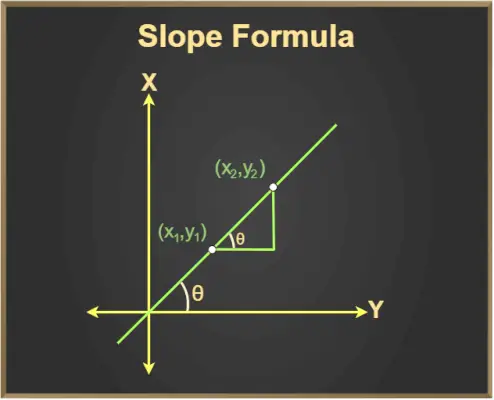
Wzór na nachylenie linii (prostej).

• Wiemy to opalenizna θ jest również nachyleniem linii, stąd nachylenie linii można również przedstawić jako,

Nachylenie (m) = tan θ = Δy/Δx

Gdzie I jest kątem utworzonym przez linię w.r.t do dodatniej osi X,

• Δy = zmiana współrzędnych y,
• Δx = zmiana współrzędnych x.

• Możemy również zdefiniować nachylenie linii jako stosunek wzniesienia względem biegu.

Nachylenie (m) = wzrost/bieg

• Niech ax + by + c = 0 będzie ogólnym równaniem prostej. Teraz wzór na nachylenie linii jest określony przez:

Nachylenie (m) = – współczynnik x / współczynnik y = -a/b

• Postać kierunkowa-przecinek linii za pomocą równania linii jest podana jako:

y = mx + do

Gdzie M jest nachyleniem linii, a c jest punktem przecięcia y linii.

Równanie nachylenia

Wzór na nachylenie służy do określenia nachylenia linii. Równanie używane do wyznaczania nachylenia zapisuje się jako:

m = tanθ = Δy/Δx = (y ₂ - I ₁ )/(X ₂ - X ₁ )

Gdzie,

• M jest nachyleniem linii
• Δy jest różnicą współrzędnych y
• Δx jest różnicą współrzędnych x
• I to kąt utworzony przez linię z dodatnią osią x

Równanie linii o nachyleniu m jest dane przez,

polecenie chown

y = mx + do

Gdzie,

• M jest nachyleniem linii
• B jest punktem przecięcia y linii

Czytaj więcej,

• Równoległe linie
• Formularz przecięcia zbocza

Przykład dotyczący wzoru na nachylenie

Przykład 1: Znajdź nachylenie linii, której współrzędne to (3, 7) i (5, 8).

Rozwiązanie:

Biorąc pod uwagę (x₁, I₁) = (3,7) i (x₂, I₂) = (5,8)

Wzór na nachylenie (m) = (y ₂ - I ₁ )/(X ₂ - X ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Zatem nachylenie danej linii wynosi 1/2.

Python konwertuje bajty na ciąg znaków

Przykład 2: Określ nachylenie linii, której współrzędne to (7, -5) i (2, -3).

Rozwiązanie:

Biorąc pod uwagę (x₁, I₁) = (7, -5) i (x₂, I₂) = (23)

Wzór na nachylenie (m) = (y ₂ - I ₁ )/(X ₂ - X ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Zatem nachylenie danej linii wynosi -2/5

Przykład 3: Znajdź wartość a, jeśli nachylenie linii przechodzącej przez punkty (-4, a) i (2, 5) wynosi 3.

Rozwiązanie:

Biorąc pod uwagę (x₁, I₁) = (4,a) i (x₂, I₂) = (2, 5) i nachylenie (m) = 3

Java do string

Wiemy, że nachylenie (m) = (y ₂ - I ₁ )/(X ₂ - X ₁ )

⇒ 3 = (5 – a)/(2 – 4)

⇒ 3 = (5 – a)/(-2)

⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11

Stąd wartość a = 11

Przykład 4: Jeśli linia tworzy kąt 60° z dodatnią osią Y, to jaka jest wartość nachylenia tej linii?

Rozwiązanie:

Biorąc pod uwagę dane, Kąt utworzony przez linię z dodatnią osią Y = 60°

Wiemy, że jeśli prosta tworzy kąt 60° z dodatnią osią Y, to tworzy z osią X kąt (90° – 60° = 30°).

Zatem wartość nachylenia linii (m) = tan 30° = 1/√3

Stąd wartość nachylenia prostej = 1/√3.

Przykład 5: Sheela sprawdzała wykres i zauważyła, że ​​podbicie wyniosło 12 jednostek, a run wyniósł 4 jednostki. Teraz oblicz nachylenie linii.

Rozwiązanie:

Biorąc pod uwagę dane, wzrost = 12 jednostek i bieg = 4 jednostki

Wiemy, że nachylenie (m) = wznoszenie/bieg

⇒ m = 12/4 = 3

Zatem nachylenie danej linii wynosi 3

Przykład 6: Znajdź nachylenie linii 3x – 7y + 8 = 0.

Rozwiązanie:

Dane dane, Równanie prostej = 3x – 7y + 8 = 0

Teraz porównaj dane z ogólnym równaniem prostej, tj. ax + by + c = 0

Dlatego a = 3, b = -7 i c = 8

Wiemy, że Nachylenie (m) = – współczynnik x/współczynnik y = -a/b

⇒ m = -3/(-7) = 3/7

Zatem nachylenie danej linii wynosi 3/7.

Ćwicz pytania dotyczące wzoru na nachylenie

Pytanie 1. Oblicz nachylenie prostej przechodzącej przez punkty (2, 3) i (5, 7)

Pytanie 2. Mając równanie prostej: y = 3x – 11, jakie jest jej nachylenie?

Pytanie 3. Jeśli nachylenie linii wynosi 5/6 i przechodzi ona przez punkt (2, 5), jakie jest równanie linii w postaci współczynnika nachylenia?

Pytanie 4. Oblicz nachylenie linii równoległej do linii (0, -3) i (1, 11)

Pytanie 5. Jeśli nachylenie linii jest nieokreślone, jakie wnioski można wyciągnąć na jej temat?

Często zadawane pytania dotyczące formuły nachylenia

Jakie jest nachylenie linii?

Nachylenie linii to wartość stromości lub nachylenia linii w płaszczyźnie x-y. Nachylenie oblicza się różnymi metodami, w zależności od tego, czy podane jest równanie linii, czy współrzędne punktów na linii.

rozmiar czcionki lateksowej

Jaki jest wzór na znalezienie nachylenia wzoru stycznego?

Nachylenie linii oblicza się za pomocą podanego wzoru. Załóżmy, że dane współrzędne dwóch punktów leżących na prostej to (x₁, I₁)/(X_2,I₂). Następnie podaje się wzór, Slope = m = tan θ = (y ₂ - I ₁ )/(X ₂ - X ₁ )

Jaka jest definicja wzoru na nachylenie?

Wzór na nachylenie definiuje się jako:

• Nachylenie = (Zmiana współrzędnej y)/(Zmiana współrzędnej x)
• Nachylenie = wznoszenie/bieg.

Jakie jest nachylenie wzoru wykresu?

Nachylenie linii jest miarą jej nachylenia względem dodatniej osi x. Matematycznie nachylenie definiuje się jako wznosić się nad biegiem .