Tarcie to siła przeciwstawiająca się ruchowi względnemu, występująca na styku ciał, ale także wewnątrz ciał, podobnie jak w przypadku płynów. Pojęcie współczynnika tarcia zostało po raz pierwszy sformułowane przez Leonarda da Vinci. Wielkość współczynnika tarcia zależy od właściwości powierzchni, otoczenia, cech powierzchni, obecności smaru itp.
Prawa tarcia
Istnieje pięć praw tarcia i są one następujące:
• Tarcie poruszającego się obiektu jest proporcjonalne i prostopadłe do siły normalnej.
• Tarcie doświadczane przez obiekt zależy od rodzaju powierzchni, z którą się styka.
• Tarcie jest niezależne od obszaru styku, o ile istnieje obszar styku.
• Tarcie kinetyczne jest niezależne od prędkości.
• Współczynnik tarcia statycznego jest większy niż współczynnik tarcia kinetycznego.
Kiedy widzimy dowolny obiekt, widzimy gładką powierzchnię, ale oglądając ten sam obiekt pod mikroskopem, można zauważyć, że nawet gładki obiekt ma ostre krawędzie. Pod mikroskopem można zobaczyć drobne wzniesienia i rowki, które nazywane są nieregularnościami powierzchni. Tak więc, gdy jeden obiekt jest przesuwany nad drugim, nierówności na powierzchni splatają się, powodując tarcie. Im większa szorstkość, tym więcej nieregularności i większa przyłożona siła.
Tarcie statyczne
Istnieje kilka teorii dotyczących przyczyn tarcia statycznego i podobnie jak większość koncepcji związanych z tarciem, każda z nich sprawdza się w pewnych warunkach, ale zawodzi w innych okolicznościach. Do zastosowań w świecie rzeczywistym (szczególnie tych związanych z maszynami przemysłowymi i ruchem). Kontroluj dwie najbardziej powszechnie akceptowane teorie tarcia statycznego, które mają związek z mikroskopijną chropowatością powierzchni.
Niezależnie od tego, jak doskonale powierzchnia jest obrobiona, wykończona i oczyszczona, nieuchronnie będzie miała nierówności – zasadniczo szorstkość, składającą się ze szczytów i dolin, podobnie jak pasmo górskie. (Technicznie rzecz biorąc, szczyty są chropowatościami.) Kiedy dwie powierzchnie stykają się, może się wydawać, że mają duży, dobrze określony obszar styku, ale w rzeczywistości kontakt występuje tylko w określonych miejscach – to znaczy tam, gdzie chropowatości obie powierzchnie kolidują.
Suma tych małych obszarów styku pomiędzy chropowatościami nazywana jest rzeczywistą lub efektywną powierzchnią styku. Ponieważ poszczególne obszary styku są bardzo małe, ciśnienie (ciśnienie = siła ÷ powierzchnia) pomiędzy powierzchniami w tych punktach jest bardzo duże. To ekstremalne ciśnienie umożliwia wystąpienie adhezji pomiędzy powierzchniami w procesie zwanym zgrzewaniem na zimno, który zachodzi na poziomie molekularnym. Zanim powierzchnie będą mogły się przesunąć względem siebie, wiązania powodujące tę adhezję muszą zostać zerwane.
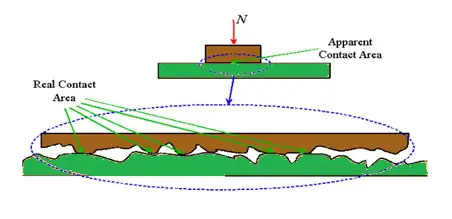
Ponadto chropowatość powierzchni oznacza, że w niektórych miejscach chropowatości jednej powierzchni osadzą się w zagłębieniach drugiej powierzchni – innymi słowy, powierzchnie będą się zazębiać.
Te powiązane ze sobą obszary muszą zostać rozerwane lub odkształcone plastycznie, zanim powierzchnie będą mogły się poruszyć. Inaczej mówiąc, musi nastąpić ścieranie. Zatem w większości zastosowań tarcie statyczne jest spowodowane zarówno przyczepnością, jak i ścieraniem stykających się powierzchni.
Prawa tarcia statycznego
Istnieją dwa prawa tarcia statycznego:
- Pierwsze prawo: Maksymalna siła tarcia statycznego nie jest zależna od powierzchni styku.
- Drugie prawo: Maksymalna siła tarcia statycznego jest porównywalna z siłą normalną, tj. jeśli siła normalna wzrasta, wzrasta również maksymalna siła zewnętrzna, jaką obiekt może wytrzymać bez ruchu.

Wyprowadzenie wzoru na tarcie statyczne
Rozważmy blok o masie mg leżący na poziomej powierzchni, jak pokazano na rysunku. Kiedy ciało naciska na powierzchnię, powierzchnia odkształca się, nawet jeśli wydaje się sztywna. Odkształcona powierzchnia popycha ciało z siłą normalną R, prostopadłą do powierzchni. Nazywa się to normalną siłą reakcji. To równoważy mg
R = mg
Rozważmy teraz, że na klocek działa siła P. Jest oczywiste, że ciało pozostaje w spoczynku, ponieważ w kierunku poziomym działa inna siła F, która przeciwstawia się przyłożonej sile P, w wyniku czego wypadkowa siła działająca na ciało wynosi zero. Siła F działająca wzdłuż powierzchni ciała stykającej się z powierzchnią stołu nazywana jest siłą tarcia.
Zatem dopóki ciało się nie porusza F = P. Oznacza to, że jeśli zwiększymy P, tarcie F również wzrośnie, pozostając zawsze równe P.
Ta siła tarcia, która działa do momentu rozpoczęcia rzeczywistego ruchu, nazywana jest tarciem statycznym.
Współczynnik tarcia statycznego
Tarcie statyczne to tarcie występujące podczas umieszczania obiektu na powierzchni. Tarcie kinetyczne wynika z ruchu obiektu na powierzchni. Tarcie dobrze charakteryzuje się współczynnikiem tarcia i wyjaśnia się jako stosunek siły tarcia do siły normalnej. Pomaga to obiektowi leżeć na powierzchni. Współczynnik tarcia statycznego jest wielkością skalarną i oznaczaną jako μS.
Wzór na współczynnik tarcia statycznego wyraża się jako
mu_{s} = frac{F}{N} Gdzie
M S = współczynnik tarcia statycznego
F = statyczna siła tarcia
N = normalna siła

Tarcie kinetyczne
Tarcie kinetyczne definiuje się jako siłę działającą pomiędzy poruszającymi się powierzchniami. Na ciało poruszające się po powierzchni działa siła działająca w kierunku przeciwnym do kierunku jego ruchu. Wielkość siły będzie zależała od współczynnika tarcia kinetycznego pomiędzy dwoma materiałami.
Tarcie można łatwo zdefiniować jako siłę, która powstrzymuje przesuwający się obiekt. Tarcie kinetyczne jest częścią wszystkiego i zakłóca ruch dwóch lub więcej obiektów. Siła działa w kierunku przeciwnym do kierunku, w którym obiekt chce się ślizgać.
Jeśli samochód musi się zatrzymać, uruchamiamy hamulce i właśnie wtedy wchodzi w grę tarcie. Idąc, gdy chce się nagle zatrzymać, tarcie oznacza ponowne podziękowanie. Ale kiedy musimy zatrzymać się w środku kałuży, sytuacja staje się trudniejsza, ponieważ tarcie jest tam mniejsze i nie może tak bardzo pomóc.

Pokonanie tarcia statycznego pomiędzy dwiema powierzchniami zasadniczo usuwa zarówno przeszkody molekularne (zgrzewanie na zimno pomiędzy nierównościami), jak i, w pewnym stopniu, przeszkody mechaniczne (interferencja pomiędzy chropowatościami i wgłębieniami powierzchni) utrudniające ruch. Po zainicjowaniu ruchu nadal występuje pewne ścieranie, ale na znacznie niższym poziomie niż podczas tarcia statycznego, a prędkość względna pomiędzy powierzchniami nie zapewnia wystarczającego czasu na wystąpienie dodatkowego zgrzewania na zimno (z wyjątkiem przypadku wyjątkowo małej prędkości).
Ponieważ większość przyczepności i ścierania została przezwyciężona w celu wywołania ruchu, opór ruchu pomiędzy powierzchniami jest zmniejszony, a powierzchnie poruszają się obecnie pod wpływem tarcia kinetycznego, które jest znacznie mniejsze niż tarcie statyczne.
Prawa tarcia kinetycznego
Istnieją cztery prawa tarcia kinetycznego:
- Pierwsze prawo: Siła tarcia kinetycznego (Fk) jest wprost proporcjonalna do reakcji normalnej (N) pomiędzy dwiema stykającymi się powierzchniami. Gdzie, M k = stała zwana współczynnikiem tarcia kinetycznego.
- Drugie prawo: Siła tarcia kinetycznego jest niezależna od kształtu i powierzchni stykających się powierzchni.
- Trzecie prawo: Zależy to od rodzaju i materiału stykającej się powierzchni.
- Czwarte prawo: Jest ona niezależna od prędkości stykającego się obiektu, pod warunkiem, że prędkość względna pomiędzy obiektem a powierzchnią nie jest zbyt duża.

Wzór tarcia kinetycznego
Współczynnik tarcia kinetycznego jest oznaczony grecką literą mu ( M ), z indeksem dolnym k. Siła tarcia kinetycznego wynosi M k razy większa od normalnej siły działającej na ciało. Wyraża się go w Newtonach (N).
Równanie tarcia kinetycznego można zapisać jako:
Siła tarcia kinetycznego = (współczynnik tarcia kinetycznego) (siła normalna)
F k = m k H
Gdzie,
F k = siła tarcia kinetycznego
M k współczynnik tarcia kinetycznego
h = siła normalna (grecka litera eta)

Wyprowadzenie wzoru na tarcie kinetyczne
Rozważmy blok ciężaru mg leżąc na poziomej powierzchni, jak pokazano na rysunku. Kiedy ciało naciska na powierzchnię, powierzchnia odkształca się, nawet jeśli wydaje się sztywna. Zdeformowana powierzchnia popycha ciało z normalną siłą R czyli prostopadle do powierzchni. Nazywa się to normalną siłą reakcji. To równoważy mg R = mg .
jquery kliknięcie
Teraz rozważmy to jako siłę P jest nakładany na blok, jak pokazano. Najwyraźniej ciało pozostaje w spoczynku z powodu jakiejś innej siły F działa w kierunku poziomym i przeciwstawia się przyłożonej sile P co skutkuje zerową siłą wypadkową działającą na ciało. Nazywa się tę siłę F działającą wzdłuż powierzchni ciała stykającej się z powierzchnią stołu siła tarcia .
Tak długo, jak ciało się nie porusza F = P . Oznacza to, że jeśli zwiększymy P, tarcie F również wzrośnie, pozostając zawsze równe P.
Gdy zwiększymy przyłożoną siłę nieco powyżej granicznego tarcia, rozpoczyna się właściwy ruch. Nie oznacza to jednak, że tarcie zniknęło. Oznacza to tylko, że siła pokonała tarcie ograniczające. Ta siła tarcia na tym etapie jest znana jako tarcie kinetyczne lub tarcie dynamiczne.
Tarcie kinetyczne lub tarcie dynamiczne to przeciwna siła, która wchodzi w grę, gdy ciało faktycznie porusza się po powierzchni innego ciała.
Zastosowanie tarcia statycznego i kinetycznego

Zastosowania tarcia statycznego
W poniższych punktach podano kilka rzeczywistych przykładów tarcia statycznego:
- Papiery na blacie stołu
- Ręcznik wiszący na wieszaku
- Zakładka w książce
- Samochód zaparkowany na wzgórzu
Zastosowania tarcia kinetycznego
W poniższych punktach podano kilka rzeczywistych przykładów tarcia kinetycznego.
- Tarcie odgrywa również ogromną rolę w codziennych sytuacjach, np. podczas pocierania dwóch przedmiotów. Powstały ruch zamienia się w ciepło, co w niektórych przypadkach powoduje pożar.
- Odpowiada również za zużycie, dlatego potrzebujemy oleju do smarowania części maszyn, ponieważ zmniejsza on tarcie.
- Kiedy dwa przedmioty pocierają się o siebie, siła tarcia zamienia się w energię cieplną, co w nielicznych przypadkach powoduje pożar
- Tarcie kinetyczne odpowiada za zużycie części maszyn, dlatego ważne jest smarowanie części maszyn olejem.
Różnica między tarciem statycznym i kinetycznym
| Tarcie statyczne | Tarcie kinetyczne |
| Tarcie statyczne to tarcie występujące pomiędzy dwoma lub większą liczbą obiektów, które nie poruszają się względem siebie | Tarcie kinetyczne to tarcie występujące pomiędzy dwoma lub większą liczbą obiektów znajdujących się w ruchu względem siebie. |
| Wielkość tarcia statycznego jest większa ze względu na większą wartość jego współczynnika. | Wielkość tarcia kinetycznego jest stosunkowo mniejsza ze względu na małą wartość jego współczynnika. |
Równanie reprezentujące tarcie statyczne jest dane przez FS= mSH | Równanie reprezentujące tarcie kinetyczne jest dane przez Fk= mkH |
| Jego wartość może wynosić zero. | Jego wartość nigdy nie może wynosić zero. |
| Przykład – ołówek na stole. | Przykład — przesuwanie ołówka po blacie stołu. |
Przykładowe problemy oparte na tarciu statycznym i kinetycznym
Pytanie 1: Mężczyzna pcha po podłodze duży karton o masie 75,0 kg.
Rozwiązanie:
Współczynnik tarcia kinetycznego wynosi μk= 0,520
Pracownik wywiera siłę 400,0 N do przodu.
Jaka jest wielkość siły tarcia?
Odpowiedź: Na płaskiej powierzchni siłę normalną obiektu można obliczyć ze wzoru
h = mg
Podstawiając wartość η w równaniu Fk= mk η, otrzymujemy
Fk= (0,520) (75,0 kg) (9,80 m/s2) = 382,2N
Pytanie 2: W powyższym pytaniu oblicz siłę wypadkową poruszającą pudło?
Rozwiązanie:
Siła wypadkowa działająca na ciało jest sumą wszystkich sił działających na to ciało.
W tym przypadku siły działające na ciało to siła wywierana przez człowieka oraz tarcie kinetyczne działające w przeciwnym kierunku.
Jeśli ruch do przodu zostanie uznany za dodatni, siłę wypadkową oblicza się w następujący sposób:
Finternet= Fpracownik- Fk
Podstawiając wartości w powyższym równaniu, otrzymujemy
Finternet= 400 N – 382,2 N = 17,8 N
Pytanie 3: Dlaczego w ruchu tocznym występuje tarcie?
Odpowiedź:
Teoretycznie piłka styka się punktowo z powierzchnią.
Jednak w rzeczywistości kula (i/lub powierzchnia) odkształca się pod wpływem obciążenia, a powierzchnia styku staje się eliptyczna.
Teoretycznie powierzchnie toczne, takie jak te występujące w większości łożysk obrotowych i liniowych (z wyjątkiem łożysk ślizgowych), nie powinny napotykać sił tarcia.
Jednak w rzeczywistych zastosowaniach trzy czynniki powodują tarcie na powierzchniach tocznych:
1. Mikropoślizg pomiędzy powierzchniami (powierzchnie przesuwają się względem siebie)
2. Właściwości niesprężyste (tj. odkształcenie) materiałów
3. Chropowatość powierzchni
Pytanie 4: Na gładkiej powierzchni umieszczono przedmiot o masie 10 kg. Tarcie statyczne pomiędzy tymi dwiema powierzchniami wyraża się jako 15 N. Znajdź współczynnik tarcia statycznego?
Rozwiązanie:
Dany
m = 10 kg
F = 15 N
MS=?
Wiemy to,
Siła normalna, N = mg
Zatem N = 10 × 9,81 = 98,1 N
Wzór na współczynnik tarcia statycznego to:
MS= 15/N
json w przykładzie jsonMS= 15/98,1
M S = 0,153
Pytanie 5: Siła normalna i siła tarcia statycznego obiektu wynoszą odpowiednio 50 N i 80 N. Znajdź współczynnik tarcia statycznego?
Rozwiązanie:
Dany
N = 50 N
F = 80 N i μS=?
Wzór na współczynnik tarcia statycznego to:
MS= F/N
MS= 80/50
MS= 1,6
Pytanie 6: Jaki jest związek pomiędzy tarciem statycznym i kinetycznym?
Odpowiedź:
Siła tarcia statycznego utrzymuje nieruchomy obiekt w spoczynku. Po pokonaniu siły tarcia statycznego, siła tarcia kinetycznego spowalnia poruszający się obiekt.
Pytanie 7: Lodówka waży 1619 N, a współczynnik tarcia statycznego wynosi 0,50. Jaka jest najmniejsza siła używana do przesuwania lodówki?
Rozwiązanie:
Podane dane:
Masa lodówki, W=1619 N
W=1619 N
Współczynnik tarcia statycznego, μS= 0,50
Minimalną siłę potrzebną do poruszenia lodówki można określić jako:
F = mSW
F = 0,50 × 1619
F = 809,50 N.
