W matematyce wszędzie istnieje implementacja linii. Jest realizowany wszędzie, tj. W geometrii, algebrze i innych. Nachylenie określa kierunek linii.
W tym artykule omówimy dwa typy nachyleń, które są nachyleniem niezdefiniowanym i nachyleniem zerowym. Zanim zrozumiemy rodzaje nachyleń, przyjrzyjmy się najpierw krótkiemu opisowi nachyleń.
Co to jest nachylenie?
Nachylenie określa stromość linii. Słowo „stromość” oznacza, jak bardzo linia jest nachylona. Innymi słowy, nachylenie pokazuje kierunek linii na płaszczyźnie współrzędnych. Dlatego jest również znany jako gradient linii. Rampa, schody itp. to tylko niektóre z rzeczywistych przykładów stoku.
W matematyce nachylenie to stosunek „wzrostu” do „przebiegu” między dwoma punktami. „Wzrost” oznacza pionową zmianę linii, a „Run” oznacza poziomą zmianę linii.
Nachylenie linii pomiędzy dwoma punktami (x1, I1) i (x2, I2) można wyznaczyć, znajdując różnicę między współrzędnymi punktów. Nachylenie linii jest zwykle oznaczane literą „m”.
m = Δx/Δy = (y2- I1)/(X2- X1)lub m = wzrost/bieg
Nieokreślone nachylenie
Nieokreślone nachylenie to nachylenie linii pionowej. Oznacza to, że jeśli linia jest pionowa, nachylenie jest nieokreślone. Linia na niezdefiniowanym nachyleniu jest równoległa do osi y, a wartość ?x wynosi 0. Współrzędna x nieokreślonego nachylenia nigdy się nie zmienia, niezależnie od współrzędnej y. W przypadku nieokreślonego nachylenia wartość Δy jest niezerową liczbą całkowitą, podczas gdy wartość Δx wynosi 0. Nieokreślone nachylenie jest przeciwne do zerowego nachylenia. Jeśli chodzi o wznoszenie i bieg, wzrost o nieokreślonym nachyleniu jest albo dodatni, albo ujemny, a przebieg o nieokreślonym nachyleniu wynosi zero.
m = Δy/Δx = dodatnie lub ujemne Δy/0Niezdefiniowana wartość m reprezentuje niezdefiniowane nachylenie i linię pionową.
Na poniższym wykresie można zobaczyć reprezentację niezdefiniowanego nachylenia. Linia na poniższym wykresie jest równoległa do osi Y, która oznacza niezdefiniowane nachylenie.
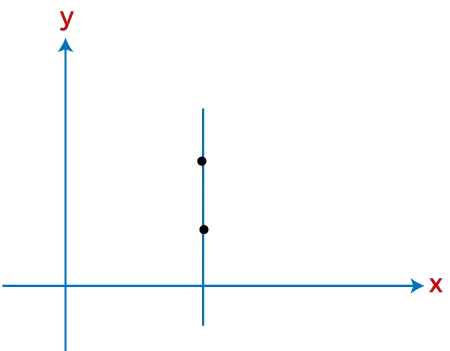
Ryc.: Reprezentacja niezdefiniowanego nachylenia
Na powyższym obrazku znajduje się pionowa linia wskazująca niezdefiniowane nachylenie.
Zerowe nachylenie
Przy zerowym nachyleniu linia jest równoległa do osi x, a współrzędna y nigdy się nie zmienia. Jest to nachylenie linii poziomej. Jeśli chodzi o wzrost i przebieg, wzrost o zerowym nachyleniu wynosi 0, a przebieg o zerowym nachyleniu jest dodatni.
m = Δy/Δx = 0/dodatni ΔxJeśli wartość m jest równa zero, linia jest pozioma i ma stałe nachylenie.
Na poniższym wykresie można zobaczyć reprezentację nachylenia zerowego. Linia na poniższym wykresie jest równoległa do osi x, która oznacza zerowe nachylenie, a y na zerowym nachyleniu pozostaje takie samo, niezależnie od tego, jakie jest x.

Ryc.: Reprezentacja zerowego nachylenia
Na powyższym obrazku widać poziomą linię wskazującą zerowe nachylenie.
Zobaczmy teraz różnicę pomiędzy nieokreślonym nachyleniem a zerowym nachyleniem.
Różnica między nieokreślonym nachyleniem a zerowym nachyleniem
Nieokreślone nachylenie jest przeciwne do nachylenia zerowego. Różnicę między nieokreślonym nachyleniem a nachyleniem zerowym zestawiono w następujący sposób:
| Tak nie. | Nieokreślone nachylenie | Zerowe nachylenie |
|---|---|---|
| 1. | Jest ona określana przez zmienną X. | Jest ona określana przez zmienną Y. |
| 2. | Jest to nachylenie linii pionowej. | Jest to nachylenie linii poziomej. |
| 3. | Nieokreślone nachylenie nie ma żadnej konkretnej wartości, więc ma wartość nieistniejącą. | Nachylenie zerowe jest ustaloną wartością, tj. Zero. |
| 4. | Mianownik niezdefiniowanego nachylenia wynosi zero. | Licznik nachylenia zerowego wynosi zero. |
| 5. | W przypadku nieokreślonego nachylenia Y zmienia się, ale X nie zmienia się. | W przypadku nieokreślonego nachylenia X zmienia się, ale Y nie zmienia się. |
To wszystko na temat artykułu. Staraliśmy się przekazać Ci wystarczające informacje w łatwiejszy sposób. Mam nadzieję, że będzie to dla Ciebie korzystne i dostarczy informacji o niezdefiniowanym nachyleniu, zerowym nachyleniu i ich porównaniu.
