Pryzmat to trójwymiarowa bryła o dwóch identycznych końcach. Składa się z płaskich boków, podobnych podstaw i równych przekrojów. Jego ściany są równoległobokami lub prostokątami bez podstaw. Taki pryzmat, który ma trzy prostokątne ściany i dwie równoległe podstawy trójkąta, nazywa się pryzmatem trójkątnym. Trójkątne podstawy są połączone bocznymi ścianami, które biegną równolegle do siebie.
Objętość wzoru na trójkątny pryzmat
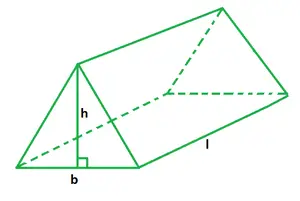
Objętość trójkątnego pryzmatu definiuje się jako przestrzeń wewnątrz niego lub przestrzeń przez nią wypełnioną. Aby obliczyć jego objętość, wystarczy znajomość pola podstawy i wysokości trójkątnego pryzmatu. Objętość trójkątnego pryzmatu jest równa iloczynowi pola podstawy i wysokości pryzmatu, zwanej również długością pryzmatu. Pole podstawy trójkątnego pryzmatu jest równe połowie iloczynu podstawy trójkąta i jego wysokości.
Formuła
V = (1/2) × b × h × l
Gdzie,
b jest podstawą trójkąta,
h jest wysokością pryzmatu,
l jest długością pryzmatu.
Przykładowe problemy
Zadanie 1. Znajdź objętość trójkątnego pryzmatu, jeśli jego podstawa wynosi 6 cm, wysokość wynosi 8 cm, a długość 12 cm.
Rozwiązanie:
Mamy b = 6, h = 8 i l = 12.
wartość logiczna w cKorzystając ze wzoru, który mamy,
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
= 3 × 8 × 12
= 288 cu. cm
Zadanie 2. Znajdź objętość trójkątnego pryzmatu, jeśli jego podstawa wynosi 5 cm, wysokość wynosi 7 cm, a długość 8 cm.
Rozwiązanie:
Amisza Patel
Mamy b = 5, h = 7 i l = 8.
Korzystając ze wzoru, który mamy,
V = (1/2) × b × h × l
= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 cu. cm
Zadanie 3. Znajdź długość trójkątnego pryzmatu, jeśli jego podstawa wynosi 6 cm, wysokość wynosi 9 cm, a objętość wynosi 98 cu. cm.
Rozwiązanie:
Mamy b = 6, h = 9 i V = 98.
Korzystając ze wzoru, który mamy,
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
usuń plik w Javie=> 196 = 27l
=> l = 196/27
=> l = 7,25 cm
Zadanie 4. Znajdź wysokość trójkątnego pryzmatu, jeśli jego podstawa wynosi 8 cm, długość 14 cm i objętość 504 cu. cm.
Rozwiązanie:
Mamy b = 8, l = 14 i V = 504.
Korzystając ze wzoru, który mamy,
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × godz. × 14
=> 504 = 56h
=> godz. = 504/56
Metoda porównania Java=> h = 9 cm
Zadanie 5. Znajdź pole podstawy trójkątnego pryzmatu, jeśli jego długość wynosi 18 cm, wysokość 10 cm i objętość 450 cu. cm.
Rozwiązanie:
Mamy l = 18, h = 10 i V = 450.
Korzystając ze wzoru na objętość mamy
V = (1/2) × b × h × l
=> 450 = (1/2) × b × 10 × 18
=> 450 = 90b
=> b = 450/90
=> b = 5 cm
Zatem pole podstawy trójkąta wynosi:
A = (1/2) × b × godz
= (1/2) × 5 × 10
= 25 cm2
