Sortowanie wiadro to technika sortowania polegająca na dzieleniu elementów na różne grupy, czyli zasobniki. Wiadra te powstają poprzez równomierne rozmieszczenie elementów. Po podzieleniu elementów na segmenty można je posortować przy użyciu dowolnego innego algorytmu sortowania. Na koniec posortowane elementy są zbierane w uporządkowany sposób.
Algorytm sortowania kubełkowego:
Tworzyć N opróżnij zasobniki (lub listy) i wykonaj następujące czynności dla każdego elementu tablicy arr[i].
- Wstaw tablicę [i] do wiadra [n* tablica [i]]
- Sortuj poszczególne segmenty za pomocą sortowania przez wstawianie.
- Połącz wszystkie posortowane zasobniki.
Jak działa sortowanie kubełkowe?
Aby zastosować sortowanie segmentowe w tablicy wejściowej [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , wykonujemy następujące kroki:
Krok 1: Utwórz tablicę o rozmiarze 10, w której każde gniazdo reprezentuje wiadro.
tablica vs lista tablic

Tworzenie wiader do sortowania
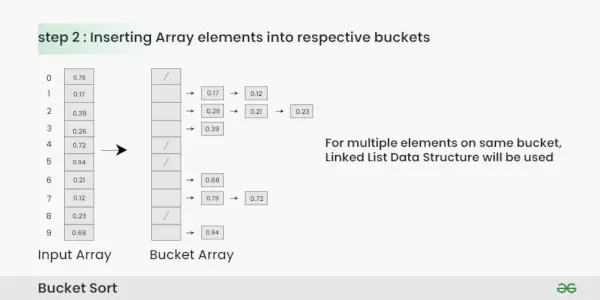
Krok 2: Wstaw elementy do segmentów z tablicy wejściowej na podstawie ich zakresu.
Wartość wyliczeniowa Java
Wkładanie elementów do wiader:
- Weź każdy element z tablicy wejściowej.
- Pomnóż element przez rozmiar tablicy segmentów (w tym przypadku 10). Na przykład dla elementu 0,23 otrzymujemy 0,23 * 10 = 2,3.
- Przekonwertuj wynik na liczbę całkowitą, co da nam indeks wiadra. W tym przypadku 2,3 jest konwertowane na liczbę całkowitą 2.
- Włóż element do wiadra odpowiadającego obliczonemu indeksowi.
- Powtórz te kroki dla wszystkich elementów tablicy wejściowej.
Wstawianie elementów Array do odpowiednich segmentów
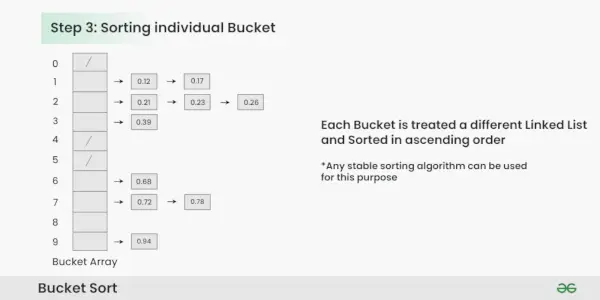
Krok 3: Sortuj elementy w każdym wiadrze. W tym przykładzie używamy szybkiego sortowania (lub dowolnego stabilnego algorytmu sortowania), aby posortować elementy w każdym segmencie.
Sortowanie elementów w każdym segmencie:
- Zastosuj stabilny algorytm sortowania (np. Sortowanie bąbelkowe, Sortowanie przez scalanie), aby posortować elementy w każdym segmencie.
- Elementy w każdym segmencie są teraz posortowane.
Sortowanie poszczególnych wiader
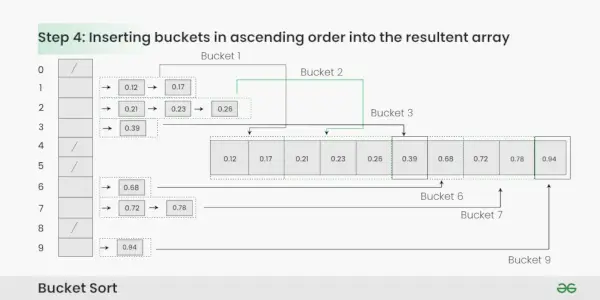
Krok 4: Zbierz elementy z każdego segmentu i umieść je z powrotem w oryginalnej tablicy.
Zbieranie elementów z każdego wiadra:
- Iteruj po kolei po każdym segmencie.
- Wstaw każdy pojedynczy element z segmentu do oryginalnej tablicy.
- Po skopiowaniu elementu jest on usuwany z zasobnika.
- Powtarzaj ten proces dla wszystkich wiader, aż wszystkie elementy zostaną zebrane.
Wstawianie segmentów w kolejności rosnącej do wynikowej tablicy
Konwersja ciągu znaków na int w Javie
Krok 5: Oryginalna tablica zawiera teraz posortowane elementy.
Ostateczna tablica posortowana przy użyciu sortowania segmentowego dla danych wejściowych to [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].
dodaj do tablicy w Javie

Zwróć posortowaną tablicę
Implementacja algorytmu sortowania kubełkowego:
Poniżej znajduje się implementacja sortowania kubełkowego:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& wiadro) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && wiadro[j]> klucz) { wiadro[j + 1] = wiadro[j]; J--; } wiadro[j + 1] = klucz; } } // Funkcja sortująca tablicę [] o rozmiarze n za pomocą sortowania segmentowego void BucketSort(float arr[], int n) { // 1) Utwórz wektor n pustych koszykówb[n]; // 2) Umieść elementy tablicy w różnych segmentach dla (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Jawa import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listwiadro) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && wiadro.get(j)> klucz) { wiadro.set(j + 1, wiadro.get(j)); J--; } wiadro.set(j + 1, klucz); } } // Funkcja sortująca tablicę [] o rozmiarze n przy użyciu sortowania segmentowego public static void BucketSort(float[] arr) { int n = arr.length; // 1) Utwórz n pustych list wiader[] segmenty = nowa ArrayList[n]; for (int i = 0; tj< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Pyton def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 i wiadro[j]> klucz: wiadro[j + 1] = wiadro[j] j -= 1 wiadro[j + 1] = klucz def wiadro_sort(arr): n = len(arr) wiadra = [[] for _ in range(n)] # Umieść elementy tablicy w różnych segmentach dla num w arr: bi = int(n * num) Bucks[bi].append(num) # Sortuj poszczególne segmenty za pomocą sortowania przez wstawianie dla segmentów w segmentach: wstawia_sort (wiadro) # Połącz wszystkie zasobniki w arr[] indeks = 0 dla zasobnika w zasobnikach: for num w zasobniku: arr[indeks] = num indeks += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,665, 0,3434] Bucket_sort (arr) print('Posortowana tablica to:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listwiadro) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && wiadro[j]> klucz) { wiadro[j + 1] = wiadro[j]; J--; } wiadro[j + 1] = klucz; } } // Funkcja sortowania tablic [] o rozmiarze n przy użyciu sortowania segmentowego static void BucketSort(float[] arr) { int n = arr.Length; // 1) Utwórz n pustych list wiader[] wiadra = nowa lista[N]; for (int i = 0; tj< n; i++) { buckets[i] = new List(); } // 2) Umieść elementy tablicy w różnych segmentach dla (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && wiadro[j]> klucz) { wiadro[j + 1] = wiadro[j]; J--; } wiadro[j + 1] = klucz; } } funkcja BucketSort(arr) { niech n = długość tablicy; niech wiadra = Array.from({length: n}, () => []); // Umieść elementy tablicy w różnych segmentach dla (let i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Wyjście
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Analiza złożoności algorytmu sortowania kubełkowego:
Złożoność czasowa: NA2),
- Jeśli założymy, że włożenie do wiadra zajmuje czas O(1), wówczas kroki 1 i 2 powyższego algorytmu wyraźnie zajmują czas O(n).
- O(1) jest łatwo możliwe, jeśli użyjemy połączonej listy do reprezentowania wiadra.
- Krok 4 również zajmuje czas O(n), ponieważ we wszystkich koszykach będzie n elementów.
- Głównym krokiem do analizy jest krok 3. Ten krok również zajmuje średnio czas O(n), jeśli wszystkie liczby są równomiernie rozłożone.
Przestrzeń pomocnicza: O(n+k)
