Prawdopodobieństwo karty to prawdopodobieństwo zdarzeń związanych z talią kart do gry. Jak wiemy, prawdopodobieństwo jest jednym z ważnych zagadnień matematyki, która zajmuje się obliczaniem możliwości wystąpienia dowolnego zdarzenia. Krótko mówiąc, prawdopodobieństwo karty to część prawdopodobieństwa, w której znajdujemy prawdopodobieństwo wyciągnięcia karty z talii kart. W tym artykule dowiemy się o prawdopodobieństwie kart ze wszystkimi szczegółami dotyczącymi wykresu prawdopodobieństwa kart, prawdopodobieństwa kart do gry, jak znaleźć prawdopodobieństwo karty i rozwiązanych przykładów prawdopodobieństwa kart. Zacznijmy naszą naukę od tematu prawdopodobieństwa kart.
Co to jest prawdopodobieństwo?
Prawdopodobieństwo to dział matematyki badający możliwość zaistnienia lub nie wystąpienia dowolnego zdarzenia. Matematycznie jest to nic innego jak stosunek liczby korzystnych wyników do całkowitej liczby wyników (przestrzeń próbki) dla zdarzenia.
Oto niektóre z rzeczywistych przykładów prawdopodobieństwa:
- Granie w gry karciane, aby znaleźć prawdopodobieństwo wygranej lub przegranej.
- Prognozowanie pogody, przewidywanie deszczu.
- Wyniki wyborów, aby określić, czy kandydat wygra, czy przegra.
- Wyniki egzaminu pozwalające określić, czy kandydat zda egzamin, czy nie.
Wzór na prawdopodobieństwo
Jeśli E będzie zdarzeniem z przestrzenią próbek S i liczba korzystnych wyników wynosi n(E), to prawdopodobieństwo zdarzenia E, tj. P(E), wyraża się wzorem:
P(E) = n(E) / n(S)
Co to jest prawdopodobieństwo karty?
Prawdopodobieństwo wyciągnięcia karty lub kolekcji kart z talii nazywa się prawdopodobieństwem karty. Krótko mówiąc, prawdopodobieństwo związane z kartami do gry nazywa się prawdopodobieństwem karty. Ponieważ jest to rodzaj prawdopodobieństwa, zawsze mieści się ono w przedziale od 0 do 1. Na przykład, jeśli mamy znaleźć prawdopodobieństwo wyciągnięcia asa z talii kart, tj. 4/52 = 1/13 [Ponieważ są 4 asy w talii 52 kart].
Talia kart w prawdopodobieństwie
Talia kart to zbiór 52 kart, które wydają się istnieć od tysięcy lat. Uważa się, że talia kart lub karty do gry pochodzą z Indii lub Chin; pierwszy udokumentowany dowód istnienia tych kart znajduje się w 9 r.t-wieczne Chiny za czasów dynastii Tang. Karty te były podobne do współczesnych kart i również dzieliły się na cztery kolory, ale nazwa i symbol tych kolorów są różne, tj. Monety, ciągi monet, miriady i miriady dziesiątek.
Obecnie karty te mają różne wzory i są podzielone na cztery kolory, a mianowicie Pik (♠), Trefl (♣), Serce (❤) i Diament (◆). Dla pojedynczej wybranej karty przestrzeń próbna wynosi 52, tj. całkowita liczba wyników dla pojedynczej wybranej karty z talii wynosi 52.
n(S) dla talii kart = 52
Rodzaje kart w talii
Każdą talię kart można klasyfikować na wiele sposobów. Niektóre parametry, według których można klasyfikować karty, to:
- Na podstawie kolorów
- Na podstawie garniturów
Rozumiemy szczegółowo tę klasyfikację w następujący sposób:
Na podstawie kolorów
Ze względu na kolory talię kart można podzielić na dwie kategorie:
- Czerwone kartki
- Czarne karty
W sumie 52 karty są podzielone równo na czerwone i czarne, co oznacza, że w talii jest 26 czerwonych i 26 czarnych kart.
Na podstawie garniturów
W talii kart znajdują się cztery kolory:
- Serca (❤)
- Diamenty (◆)
- Kluby (♣)
- Piki (♠)
Oprócz nich istnieje jeszcze jedna klasyfikacja kart, oparta na randze kart:
- As
- Karty liczbowe
- Karty twarzy
As
As to jedna z takich kart, która jest albo najważniejsza, albo najmniej ważna w zależności od gry. Na tej karcie jest napisane A, a każdy kolor ma jedną taką kartę, czyli cztery asy.
Karty liczbowe
Od 2 do 10, w każdym kolorze jest 9 kart, co daje w sumie 36 takich kart.
Karty twarzy
Karty twarzy, jak sama nazwa wskazuje, zawierają figurę lub twarz figurki na karcie. Istnieją trzy karty w każdym kolorze, tj. Walet, Dama, Król. Zatem w sumie mamy 12 kart z figurami.
Wszystkie te klasyfikacje można zobaczyć w poniższej tabeli.
| Talia kart (52 karty) | ||||
|---|---|---|---|---|
| Kolorowe karty | Czarne karty (26 kart) | Czerwone kartki (26 kart) | ||
| Garnitury | Pik (13 kart) | Klub (13 kart) | Serce (13 kart) | Diament (13 kart) |
| Karty twarzy (12 kart w talii i 3 karty w każdym kolorze) | K. (król) | K. (król) | K. (król) | K. (król) |
| Q (królowa) | Q (królowa) | Q (królowa) | Q (królowa) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Karty liczbowe (36 kart w talii i 9 kart w kolorze) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Karty Asów (4 karty w talii i 1 karta w kolorze) | A (As) | A (As) | A (As) | A (As) |
Wykres talii kart
Poniższa tabela przedstawia klasyfikację talii kart do gry:
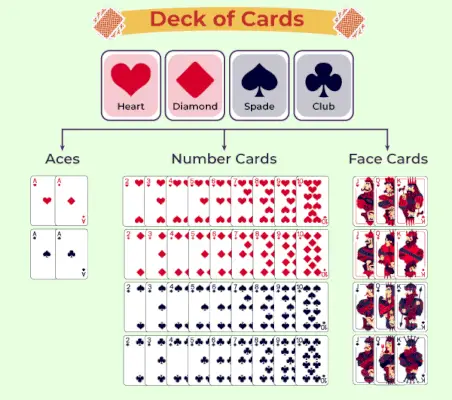
Prawdopodobieństwo karty do gry
Niektóre z typowych zdarzeń w prawdopodobieństwie kart omówiono w poniższej tabeli:
| Wydarzenie E za dobranie karty | Prawdopodobieństwo P(E) |
|---|---|
| As | P(E) = 4/52 = 1/13 |
| Król alfabet jako cyfry | P(E) = 4/52 = 1/13 |
| Karta liczbowa | P(E) = 36/52 = 9/13 |
| Karta twarzy | P(E) = 12/52 = 3/13 |
| Karta pik | P(E) = 13/52 = 1/4 |
| Czerwona kartka | P(E) = 26/52 = 1/2 |
Jak znaleźć prawdopodobieństwo kart?
Kroki, aby znaleźć prawdopodobieństwo zdarzeń związanych z kartami, są takie same, jak w przypadku wszystkich innych prawdopodobieństw, które są podane w następujący sposób:
Krok 1: Najpierw znajdź liczbę korzystnych wyników z danego pytania.
Krok 2: Następnie znajdź całkowitą liczbę wyników.
Krok 3: Zastosuj wzór na prawdopodobieństwo, aby znaleźć prawdopodobieństwo karty.
Przykład: Jakie jest prawdopodobieństwo wylosowania asa z talii kart?
Odpowiedź:
Tutaj E jest zdarzeniem wyciągnięcia karty asa
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie asa z talii = 4 (w 1 talii znajdują się 4 asy)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1/13
Prawdopodobieństwo wyciągnięcia asa = 1/13
Przykładowe pytania dotyczące prawdopodobieństwa kart
Zadanie 1: Jakie jest prawdopodobieństwo wylosowania następujących kart z talii kart?
(i) łopata
(ii) czarna kartka
(iii) karta numeryczna
Rozwiązanie:
(i) Tutaj E jest zdarzeniem losowania karty pik
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = wyciągnięcie karty pik z talii = 13 (w 1 talii znajduje się 13 kart w każdym kolorze)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1/4
Prawdopodobieństwo wylosowania pik = 1/4
(ii) Tutaj E jest zdarzeniem wyciągnięcia czarnej karty
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie czarnej karty z talii = 26 (w 1 talii znajduje się 26 czarnych kart)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1/2
Prawdopodobieństwo wyciągnięcia czarnej karty = 1/2
(iii) Tutaj E jest zdarzeniem losowania karty z numerem
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = losowanie karty z liczbą z talii = 36 (w 1 talii znajduje się 36 kart z liczbami)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9/13
Prawdopodobieństwo wylosowania karty z numerem = 9/13
Zadanie 2: Jakie jest prawdopodobieństwo wylosowania następujących kart z talii kart?
(i) Król lub czarna karta
(ii) Czerwona karta i as
Rozwiązanie:
(i) Tutaj E oznacza wyciągnięcie króla lub czarnej karty
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie króla lub czarnej karty z talii = 26 + 2 = 28 (Jest 26 czarnych kart, z których 2 to król, a pozostałych 2 czarnych królów w 1 talii)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7/13
Prawdopodobieństwo wylosowania króla lub czarnej karty = 7/13
(ii) Tutaj E oznacza wyciągnięcie czerwonej karty i asa
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie czerwonej karty i asa z talii = 2 (Jest 26 czerwonych kart, w tym 2 to asy)
Zgodnie z pytaniem wylosowana karta powinna być czerwona i as. Zatem n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1/26
Prawdopodobieństwo wyciągnięcia czerwonej i asa wynosi 1/26
Zadanie 3: Jakie jest prawdopodobieństwo wylosowania następujących kart z talii kart?
(i) Karta nieklubowa
(ii) Karta bez twarzy
Rozwiązanie:
(i) Tutaj E jest zdarzeniem wyciągnięcia karty nieklubowej
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie karty nieklubowej z talii = 39 (w 1 talii znajduje się 13 treflów, nie-talia = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3/4
Prawdopodobieństwo wyciągnięcia karty nieklubowej = 3/4
(ii) Tutaj E jest zdarzeniem losowania karty innej niż twarz
Całkowita liczba wyników w talii n(S) = 52
Liczba korzystnych wyników = n(E) = dobranie karty bez twarzy z talii = 40 (w 1 talii znajduje się 12 kart z figurami, nie-talia = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40 / 52
P(E) = 10 / 13
Prawdopodobieństwo wyciągnięcia karty nieklubowej = 10/13
Zadanie 4: Jakie jest prawdopodobieństwo, że wylosujemy kartę, która nie jest ani czerwona, ani figurowa?
Rozwiązanie:
Tutaj E oznacza wyciągnięcie ani czerwonej, ani figury
Całkowita liczba wyników w talii n(S) = 52
architektura LinuksaLiczba korzystnych wyników = n(E) = nie losowanie ani czerwonej, ani figury z talii.
Suma czerwonych kartek = 26
W talii znajduje się łącznie 12 kart z figurami, ale 6 czerwonych kart z figurami zostało już usuniętych. Zatem pozostałe figury = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Prawdopodobieństwo wylosowania ani czerwonej, ani figury = 8 / 13
Zadanie 5: Jakie jest prawdopodobieństwo wylosowania dwóch kart z talii kart z uzupełnieniem, gdy pierwszą kartą jest kier, a drugą karo?
Rozwiązanie:
Prawdopodobieństwo wyciągnięcia pierwszej karty jako serca = 13/52
Po dobraniu pierwszej karty, karta jest usuwana.
Prawdopodobieństwo wyciągnięcia drugiej karty jako karo = 13/51
Prawdopodobieństwo wyciągnięcia pierwszej karty jako kier, a drugiej jako karo = (13/52) × (13/51)
Prawdopodobieństwo wyciągnięcia pierwszej karty jako kier, a drugiej jako karo = 13/204
Często zadawane pytania dotyczące prawdopodobieństwa kart
1. Co to jest prawdopodobieństwo karty?
Prawdopodobieństwo wylosowania karty z talii kart nazywa się prawdopodobieństwem karty.
2. Wypisz rodzaje kolorów w talii kart.
W talii kart występują cztery rodzaje kolorów. Oni są:
- Kiery
- Diamenty
- Pik
- Kluby
3. Jakie jest przykładowe miejsce na talię kart, gdy z talii zostanie dociągnięta jedna karta?
Próbna przestrzeń talii kart, gdy zostanie wylosowana jedna karta, zawiera 52 wyniki.
4. Napisz wzór na znalezienie prawdopodobieństwa.
Wzór na znalezienie prawdopodobieństwa jest określony wzorem:
Prawdopodobieństwo zdarzenia = Liczba korzystnych zdarzeń / Całkowita liczba wyników
LUB
P(E) = n(E) / n(S)
5. Ile kart twarzy znajduje się w talii kart?
W talii kart znajduje się 12 figur.
