Liczby zespolone są naturalną kontynuacją liczb rzeczywistych. W dzisiejszych czasach liczby zespolone są wykorzystywane w wielu dziedzinach, takich jak cyfrowe przetwarzanie sygnałów, kryptografia i wiele dziedzin związanych z komputerami.

W tym artykule dowiemy się o liczbach urojonych, liczbach zespolonych i ich typach, różnych operacjach na liczbach zespolonych, właściwościach liczb zespolonych, zastosowaniu liczb zespolonych itp.

Definicja liczb zespolonych

Liczby zespolone są liczby formularza (a + ja b) Gdzie A & B są liczbami rzeczywistymi i I jest urojoną jednostką zwaną jotą, która reprezentuje √-1. Na przykład 2 + 3i jest liczbą zespoloną, w której 2 jest liczbą rzeczywistą, a 3i jest liczbą urojoną. Liczby zespolone można zapisać jako a + ib, gdzie a i b są liczbami wymiernymi, które można przedstawić na osi liczbowej rozciągającej się do nieskończoność .

Moduł liczby zespolonej

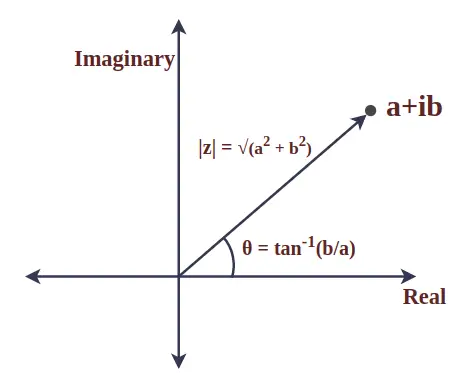
Moduł liczby zespolonej jest wartością bezwzględną i reprezentuje odległość pomiędzy początkiem układu a danym punktem. Jest również znana jako wielkość liczby zespolonej. Rozważmy liczbę zespoloną z = a + ib, wówczas moduł z definiuje się jako:

|z| = √(a ² + b ² )

Gdzie,

• A jest rzeczywistą częścią liczby zespolonej z, oraz
• B jest urojoną częścią liczby zespolonej z.

Argument liczby zespolonej

Kąt między wektorem promienia liczby zespolonej a dodatnią osią x nazywany jest argumentem liczby zespolonej. Dla liczby zespolonej z = a + ib jest ona matematycznie dana wzorem:

θ = opalenizna ^-1 (b/a)

Gdzie,

• A jest rzeczywistą częścią liczby zespolonej z, oraz
• B jest urojoną częścią liczby zespolonej z.

Potęga i (jota)

I(iota) definiuje się jako pierwiastek kwadratowy z -1. Zatem dowolną potęgę i można wyrazić jako wielokrotne pomnożenie i przez samo, tj.

• ja = √(-1)
• I²= -1
• I³= – tj
• I⁴= 1
• I⁵= ja
• I⁶= – 1
• i tak dalej..

Potrzeba liczb zespolonych

W starożytności ludzie znali jedynie liczby naturalne liczby są z natury najbardziej intuicyjne, ponieważ ludzki mózg już je rozumie, korzystając z wizualizacji takich rzeczy, jak owce i jedzenie. Zatem mamy tylko zbiór liczb naturalnych ( N ), ale w liczbach naturalnych nie ma rozwiązania równania x + a = b (a> b) i a, b ∈ N. W ten sposób powstało rozszerzenie liczb naturalnych, tj. Integers( I ).

Ponownie w tym zestawie liczb nie ma rozwiązania równania ax = b (a ≠ 0) i a, b ∈ I, gdzie oba a i b są liczbami całkowitymi. Zatem zbiór liczb całkowitych (I) zostaje rozszerzony na zbiór liczb wymiernych ( Q ).

podwójne w Javie

Ponownie, w tym zbiorze liczb wymiernych nie ma rozwiązania równania x²= a (a> 0) i a ∈ Q. Zatem Q jest rozszerzony o liczby takie, jak x²= a(dla a> 0), tj. liczby niewymierne. Zbiór ten nosi nazwę Liczby rzeczywiste i jest reprezentowany przez R .

Przez długi czas uważano, że nie musimy rozszerzać tego zbioru liczb rzeczywistych, aby utworzyć inny, większy zbiór, ponieważ ten zbiór liczb wydaje się kompletny. Ale znowu pojawił się nowy problem w tym zbiorze liczb, tj. nie ma liczby rzeczywistej takiej, jak x²= a (a <0) i a ∈ R. Zatem zbiór liczb rzeczywistych jest dalej rozszerzany, aby objąć wszystkie tak cenione i nazwane liczby zespolone tego zbioru i jest reprezentowany przez C .

Klasyfikacja liczb zespolonych

Jak wiemy, standardowa postać liczby zespolonej to z = (a + ja b) gdzie a, b ∈ R i i to jota (jednostka urojona). Zatem w zależności od wartości a (zwanej częścią rzeczywistą) i b (zwaną częścią urojoną) liczby zespolone dzieli się na cztery typy:

• Zerowa liczba zespolona
• Liczby czysto rzeczywiste
• Liczby czysto urojone
• Liczby urojone

Przyjrzyjmy się szczegółowo tym typom.

Zerowa liczba zespolona

Dla dowolnej liczby zespolonej z = a + ib, jeśli a = 0 i b = 0, liczba zespolona nazywana jest zerową liczbą zespoloną. Na przykład jedynym tego przykładem jest 0.

Liczby czysto rzeczywiste

Dla dowolnej liczby zespolonej z = a + ib, jeśli a ≠ 0 i b = 0, wówczas liczbę zespoloną nazywa się liczbą czysto rzeczywistą, tj. liczbą bez części urojonej. Wszystkie liczby rzeczywiste są tego przykładami, takimi jak 2, 3, 5, 7 itd.

Liczby czysto urojone

Dla dowolnej liczby zespolonej z = a + ib, jeśli a = 0 i b ≠ 0, wówczas liczbę zespoloną nazywamy liczbą czysto urojoną, tj. liczbą bez części rzeczywistej. Wszystkie liczby bez części rzeczywistych są przykładami tego typu liczb, tj. -7i, -5i, -i, i, 5i, 7i itd.

Liczby urojone

Dla dowolnej liczby zespolonej z = a + ib, jeśli a ≠ 0 i b ≠ 0, wówczas liczbę zespoloną nazywa się liczba urojona . Na przykład (-1 – i), (1 + i), (1 – i), (2 + 3i) itd.

Różne formy liczb zespolonych

Istnieją różne formy liczb zespolonych, które są,

• Forma prostokątna
• Forma polarna
• Forma wykładnicza

Teraz poznamy je szczegółowo.

Forma prostokątna

Forma prostokątna Jest nazywane również Forma standardowa i jest reprezentowany przez (a + ib), gdzie aib są liczbami rzeczywistymi.

Na przykład: (5 + 5i), (-7i), (-3 – 4i) itd.

Forma polarna

Forma polarna jest reprezentacją liczby zespolonej, gdzie współrzędne biegunowe [gdzie współrzędne są reprezentowane jako (r, θ), gdzie r jest odległością od początku, a θ jest kątem między linią łączącą punkt i początek a dodatnią osią x) służą do reprezentowania liczby zespolonej. Każda liczba zespolona jest reprezentowana jako r [cos θ + i sin θ].

Na przykład: [cos π/2 + i sin π/2], 5 [cos π/6 + i sin π/6] itd.

Forma wykładnicza

Formy wykładnicze liczb zespolonych jest reprezentacją liczb zespolonych za pomocą wzoru Eulera i w tej formie liczba zespolona jest reprezentowana przez re^I, gdzie r jest odległością punktu od początku układu współrzędnych, a θ jest kątem pomiędzy dodatnią osią x a wektorem promienia.

Dla przykładów: np^ja(0), To jest^ja(π/2), 5.tj^ja(π/6)itp.

Notatka: Wszystkie trzy formy liczb zespolonych omówione powyżej są wzajemnie konwertowalne, co oznacza, że ​​można je bardzo łatwo przekształcić z jednej postaci na drugą.

Operacje na liczbach zespolonych

Na liczbach zespolonych można wykonać następujące operacje:

• Dodatek
• Odejmowanie
• Mnożenie
• Dział
• Koniugacja

Dodawanie liczb zespolonych

Możemy dodać dwie liczby zespolone, po prostu dodając osobno ich części rzeczywiste i urojone.

Na przykład (3 + 2i) + (1 + 4i) = 4 + 6i.

Odejmowanie liczb zespolonych

Możemy odjąć dwie liczby zespolone, po prostu odejmując osobno ich część rzeczywistą i urojoną.

Na przykład (3 + 2i) – (1 + 4i) = 2 – 2i.

Mnożenie liczb zespolonych

Możemy pomnożyć dwie liczby zespolone, korzystając z własności rozdzielności i faktu, że i²= -1.

Na przykład (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Podział liczb zespolonych

Możemy podzielić jedną liczbę zespoloną przez drugą, po prostu mnożąc licznik i mianownik przez zespoloną koniugat mianownika, co jeszcze bardziej upraszcza wyrażenie.

Na przykład (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Koniugacja liczb zespolonych

Z łatwością znajdziemy tzw koniugacja liczby zespolonej, po prostu zmieniając znak jego części urojonej. Koniugat liczby zespolonej jest często oznaczany kreską nad liczbą, na przykład z̄.

Na przykład koniugat 3 + 2i to 3 – 2i.

Tożsamości liczb zespolonych

Dla dowolnych dwóch liczb zespolonych z₁i z₂można podać następujące tożsamości algebraiczne:

• (z ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (z ₁ – z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (z ₁ ) ² – (z ₂ ) ² = (z ₁ + z ₂ )(z ₁ – z ₂ )
• (z ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² z ₂ +3(z ₂ ) ² z ₁ + (z ₂ ) ³
• (z ₁ – z ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² z ₂ +3(z ₂ ) ² z ₁ – (z ₂ ) ³

Wzory związane z liczbami zespolonymi

Istnieje kilka formuł związanych z liczbami zespolonymi, niektóre z nich są następujące:

funkcja chr w Pythonie

Wzór Eulera

Wzór Eulera pokazuje związek między potęgą urojoną wykładnika a stosunkiem trygonometrycznym sin i cos i jest określony wzorem:

To jest ^IX = cos x + ja grzech x

Formuła De Moivre’a

Formuła De Moivre’a wyraża n^tpotęga liczby zespolonej w postaci biegunowej i jest dana wzorem:

(bo x + ja grzech x) ^N = cos(nx) + ja grzech(nx)

Złożona płaszczyzna

Płaszczyzna, na której liczby zespolone są jednoznacznie reprezentowane, nazywana jest płaszczyzną zespoloną, płaszczyzną Arganda lub płaszczyzną Gaussa.

Płaszczyzna złożona ma dwie osie:

• Oś X lub oś rzeczywista
• Oś Y lub oś urojona

Oś X lub oś rzeczywista

• Wszystkie czysto rzeczywiste liczby zespolone są jednoznacznie reprezentowane przez punkt.
• Część rzeczywista Re(z) wszystkich liczb zespolonych jest wykreślana względem niej.
• Dlatego też nazywa się oś X Prawdziwa oś .

Oś Y lub oś urojona

• Wszystkie czysto urojone liczby zespolone są jednoznacznie reprezentowane przez znajdujący się na nich punkt.
• Część urojona Im(z) wszystkich liczb zespolonych jest wykreślana względem niej.
• Dlatego też nazywa się oś Y Wyimaginowana oś .

Geometryczna reprezentacja liczb zespolonych

Jak wiemy, każda liczba zespolona (z = a + i b) jest reprezentowana przez unikalny punkt p(a, b) na płaszczyźnie zespolonej, a każdy punkt na płaszczyźnie zespolonej reprezentuje unikalną liczbę zespoloną.

Aby przedstawić dowolną liczbę zespoloną z = (a + i b) na płaszczyźnie zespolonej, postępuj zgodnie z następującymi konwencjami:

• Część rzeczywista z (Re(z) = a) staje się współrzędną X punktu p

• Część urojona z (Im(z) = b) staje się współrzędną Y punktu p

I wreszcie z (a + i b) ⇒ p (a, b), które jest punktem na płaszczyźnie zespolonej.

Właściwości liczb zespolonych

Istnieją różne właściwości liczb zespolonych, a niektóre z nich są następujące:

• Dla dowolnej liczby zespolonej z = a + ib, jeśli z = 0, to a = 0 oraz b = 0.
• Dla 4 liczb rzeczywistych a, b, c i d takich, że z₁= a + ib i z₂= c + identyfikator. Jeśli z₁= z₂wówczas a = c i b = d.
• Dodanie liczby zespolonej do jej koniugatu daje liczbę czysto rzeczywistą, tj. z + z̄ = liczba rzeczywista.

Niech z = a + ib,

z + z̄ = a + jeden + a – jeden

⇒ z + z̄ = 2a (co jest całkowicie rzeczywiste)

• Iloczyn liczby zespolonej z wynikami sprzężonymi jest również liczbą czysto rzeczywistą, tj. z × z̄ = liczba rzeczywista

Niech więc z = a + ib

z × z̄ = (a + jeden) × (a – jeden)

⇒ z × z̄= a²- I²B²

⇒ z × z̄ = a²+ b²(co jest całkowicie prawdziwe)

• Liczby zespolone są przemienne w ramach operacji dodawania i mnożenia. Rozważmy dwie liczby zespolone z₁i z₂, i wtedy

z ₁ +z ₂ = z ₂ +z ₁

z ₁ × z ₂ = z ₂ × z ₁

• Liczby zespolone są asocjacyjny z działaniem dodawania i mnożenia. Rozważmy trzy liczby zespolone z₁, z₂i z₃Następnie

(z ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(z ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Liczby zespolone posiadają własność rozdzielcza mnożenia zamiast dodawania. Rozważmy trzy liczby zespolone z₁, z₂i z₃Następnie

z ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Czytaj więcej,

• Dzielenie liczb zespolonych
• Pasek Z w liczbach zespolonych

Przykłady na liczbach zespolonych

Przykład 1: Wykreśl liczby zespolone z = 3 + 2i na płaszczyźnie zespolonej.

Rozwiązanie:

Dany:

z = 3 + 2 ja

Zatem punktem jest z(3, 2). Teraz nanosimy ten punkt na poniższy wykres, tutaj na tym wykresie oś x przedstawia część rzeczywistą, a oś y przedstawia część urojoną.

Przykład 2: Wykreśl liczby zespolone z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) na płaszczyźnie zespolonej.

Rozwiązanie:

Dany:

z₁= (2 + 2 ja)

z₂= (-2 + 3 ja)

z₃= (-1 – 3 ja)

z₄= (1 – ja)

Zatem punkty to z₁(2, 2), z₂(-2, 3), z₃(-1, -3) i z₄(1, -1). Teraz nanosimy te punkty na poniższy wykres, tutaj oś x przedstawia część rzeczywistą, a oś y przedstawia część urojoną.

Często zadawane pytania dotyczące liczb zespolonych

Zdefiniuj liczby zespolone.

Liczby w postaci a+ib nazywane są liczbami zespolonymi, gdzie aib są liczbą rzeczywistą, a i jest jednostką urojoną reprezentującą pierwiastek kwadratowy z -1.

Jaka jest różnica między liczbą rzeczywistą a liczbą zespoloną?

Różnica między liczbami rzeczywistymi i zespolonymi polega na tym, że potrzebujemy tylko jednej liczby, aby przedstawić dowolną liczbę rzeczywistą, ale potrzebujemy dwóch liczb rzeczywistych, aby przedstawić dowolną liczbę zespoloną.

Jaka jest część rzeczywista i urojona liczby zespolonej?

W liczbie zespolonej a + ib a jest częścią rzeczywistą liczby zespolonej, a b nazywa się częścią urojoną liczby zespolonej.

Jaki jest złożony koniugat liczby zespolonej?

Dla liczby zespolonej a + ib, a – ib nazywa się jej sprzężeniem zespolonym. Złożone koniugaty można znaleźć po prostu zmieniając znak części urojonej.

Jaki jest moduł liczby zespolonej?

Odległość między początkiem a punktem reprezentowanym przez liczbę zespoloną na płaszczyźnie Arganda nazywana jest modułem tej liczby całkowitej i dla z = a + ib jest matematycznie obliczana przez:

|z| = √(a ² + b ² )

Zastępowanie metody w Javie

Jaki jest argument liczby zespolonej?

Kąt między wektorem promienia liczby zespolonej a dodatnią osią x nazywany jest argumentem liczby zespolonej i dla z = a + ib jest matematycznie podawany wzorem:

θ = opalenizna ^-1 (b/a)

Jaka jest postać polarna liczby zespolonej?

Dla dowolnej liczby zespolonej z = a + ib jej postać biegunową wyraża się wzorem:

r [cos θ + ja sin θ]

Jaki jest wzór Eulera?

Wzór Eulera pokazuje związek między potęgą urojoną wykładnika a stosunkiem trygonometrycznym sin i cos i jest określony wzorem:

To jest ^IX = cos x + ja grzech x