NFA może mieć zero, jeden lub więcej ruchów z danego stanu na danym symbolu wejściowym. NFA może również mieć ruchy NULL (ruchy bez symbolu wejściowego). Z drugiej strony DFA ma jeden i tylko jeden ruch z danego stanu na danym symbolu wejściowym.

Kroki konwersji NFA na DFA:

Krok 1: Przekonwertuj podany NFA na równoważną tabelę przejściową
Aby przekonwertować NFA na równoważną tabelę przejść, musimy wypisać wszystkie stany, symbole wejściowe i reguły przejścia. Reguły przejścia są reprezentowane w postaci macierzy, gdzie wiersze reprezentują bieżący stan, kolumny reprezentują symbol wejściowy, a komórki reprezentują następny stan.

Krok 2: Utwórz stan początkowy DFA
Stan początkowy DFA to zbiór wszystkich możliwych stanów początkowych w NFA. Zbiór ten nazywa się domknięciem epsilon stanu początkowego NFA. Zamknięcie epsilon to zbiór wszystkich stanów, do których można dojść ze stanu początkowego, wykonując przejścia epsilon (?).

Krok 3: Utwórz tabelę przejściową DFA
Tabela przejść DFA jest podobna do tabeli przejść NFA, ale zamiast pojedynczych stanów, wiersze i kolumny reprezentują zestawy stanów. Dla każdego symbolu wejściowego odpowiednia komórka w tabeli przejść zawiera zamknięcie epsilon zbioru stanów uzyskanych poprzez przestrzeganie reguł przejścia w tabeli przejść NFA.

Krok 4: Utwórz końcowe stany DFA
Stany końcowe DFA to zbiory stanów, które zawierają co najmniej jeden stan końcowy z NFA.

Krok 5: Uprość DFA
DFA uzyskany w poprzednich krokach może zawierać niepotrzebne stany i przejścia. Aby uprościć DFA, możemy zastosować następujące techniki:

• Usuń nieosiągalne stany: stany, do których nie można dotrzeć ze stanu początkowego, można usunąć z DFA.
• Usuń stany martwe: Stany, które nie mogą doprowadzić do stanu końcowego, można usunąć z DFA.
• Połącz równoważne stany: Stany, które mają te same zasady przejścia dla wszystkich symboli wejściowych, można połączyć w jeden stan.

Krok 6: Powtarzaj kroki 3-5, aż dalsze uproszczenia nie będą już możliwe
Po uproszczeniu DFA powtarzamy kroki 3-5, aż dalsze uproszczenia nie będą już możliwe. Ostateczny otrzymany DFA jest zminimalizowanym odpowiednikiem DFA danego NFA.

Numer 1 milion

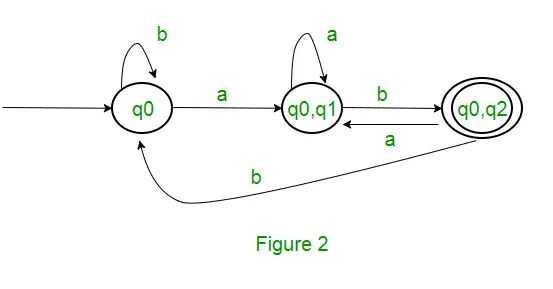
Przykład: Rozważmy następujący NFA pokazany na rysunku 1.

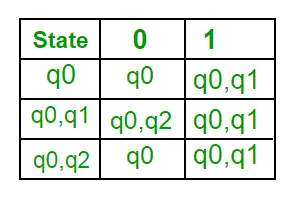
Poniżej przedstawiono różne parametry NFA. Q = {q0, q1, q2}? = ( za, b ) fa = { q2 }? (Funkcja przejścia NFA)

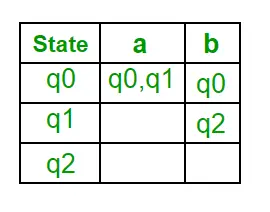
Krok 1: Q’ =? Krok 2: Q’ = {q0} Krok 3: Dla każdego stanu w Q’ znajdź stany dla każdego symbolu wejściowego. Obecnie stan w Q’ to q0, znajdź ruchy od q0 na symbolu wejściowym aib, używając funkcji przejścia NFA i zaktualizuj tabelę przejść DFA. ?” (Funkcja przejścia DFA)

Teraz { q0, q1 } będzie traktowane jako pojedynczy stan. Ponieważ jego wpisu nie ma w Q’, dodaj go do Q’. Zatem Q' = { q0, { q0, q1 } } Teraz ruchy ze stanu { q0, q1 } na różnych symbolach wejściowych nie są obecne w tabeli przejść DFA, obliczymy to w następujący sposób: ?' ( { q0, q1 } , a) =? (q0, a)? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) =? (q0, b)? ? ( q1, b ) = { q0, q2 } Teraz zaktualizujemy tabelę przejściową DFA. ?” (Funkcja przejścia DFA)

Teraz { q0, q2 } będzie traktowane jako pojedynczy stan. Ponieważ jego wpisu nie ma w Q’, dodaj go do Q’. Zatem Q' = { q0, { q0, q1 }, { q0, q2 } } Teraz ruchy ze stanu {q0, q2} na różnych symbolach wejściowych nie są obecne w tabeli przejść DFA, obliczymy to w następujący sposób: ?' ( { q0, q2 }, a ) =? (q0, a)? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) =? (q0, b)? ? ( q2, b ) = { q0 } Teraz zaktualizujemy tabelę przejściową DFA. ?” (Funkcja przejścia DFA)

przykładowy JavaScript

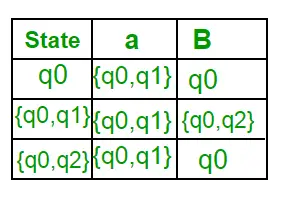
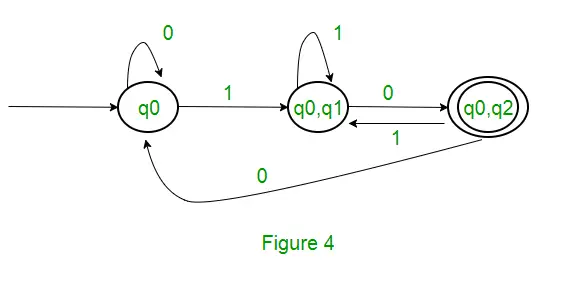
Ponieważ nie jest generowany żaden nowy stan, konwersję zakończyliśmy. Stanem końcowym DFA będzie stan, którego składową jest q2, tj. {q0, q2} Poniżej przedstawiono różne parametry DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } }? = ( a, b ) F = { { q0, q2 } } i funkcja przejścia ?’, jak pokazano powyżej. Ostateczny wynik DFA dla powyższego NFA pokazano na rysunku 2.

Notatka : Czasami nie jest łatwo przekonwertować wyrażenie regularne na DFA. Najpierw możesz przekonwertować wyrażenie regularne na NFA, a następnie NFA na DFA.

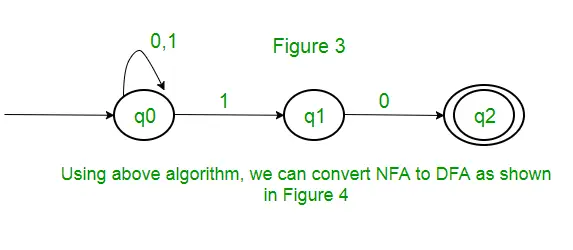
Pytanie : Liczba stanów w minimalnym deterministycznym automacie skończonym odpowiadającym wyrażeniu regularnemu (0 + 1)* (10) wynosi ____________.

Rozwiązanie : Najpierw utworzymy NFA dla powyższego wyrażenia. Aby utworzyć NFA dla (0 + 1)*, NFA będzie w tym samym stanie q0 na symbolu wejściowym 0 lub 1. Następnie w celu konkatenacji dodamy dwa ruchy (q0 do q1 dla 1 i q1 do q2 dla 0), jak pokazano na rysunku 3.

Ten artykuł został napisany przez Sonal Tuteja.