Warunek wstępny – Data Mining, miara podobieństwa odnosi się do odległości o wymiarach reprezentujących cechy obiektu danych w zbiorze danych. Jeśli odległość ta będzie mniejsza, stopień podobieństwa będzie wysoki, natomiast gdy odległość będzie duża, stopień podobieństwa będzie niski. Niektóre z popularnych miar podobieństwa to:
- Odległość euklidesowa.
- Odległość Manhattanu.
- Podobieństwo Jaccarda.
- Odległość Minkowskiego.
- Cosinus podobieństwa.
Cosinus podobieństwo to metryka pomocna w określeniu podobieństwa obiektów danych niezależnie od ich rozmiaru. Możemy zmierzyć podobieństwo między dwoma zdaniami w Pythonie za pomocą podobieństwa cosinusowego. W przypadku podobieństwa cosinus obiekty danych w zbiorze danych są traktowane jak wektor. Wzór na znalezienie cosinusa podobieństwa między dwoma wektorami to –
(x, y) = x . y / ||x|| ||y||>
Gdzie,
- X . y = iloczyn (kropka) wektorów „x” i „y”.||x|| I ||i|| = długość (wielkość) dwóch wektorów „x” i „y”.||x||
||i|| = iloczyn regularny dwóch wektorów „x” i „y”. Przykład : Rozważmy przykład znalezienia podobieństwa między dwoma wektorami – 'X' I 'I' , korzystając z podobieństwa cosinusa. Wektor „x” ma wartości, x = { 3, 2, 0, 5 } Wektor „y” ma wartości, y = { 1, 0, 0, 0 } Wzór na obliczenie podobieństwa cosinusa jest następujący: 
(x, y) = x. y / ||x|| ||i||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Odmienność między dwoma wektorami „x” i „y” jest określona wzorem –
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Cosinus podobieństwa między dwoma wektorami mierzy się w „θ”.
- Jeśli θ = 0°, wektory „x” i „y” pokrywają się, co dowodzi, że są podobne.
- Jeśli θ = 90°, wektory „x” i „y” są różne.
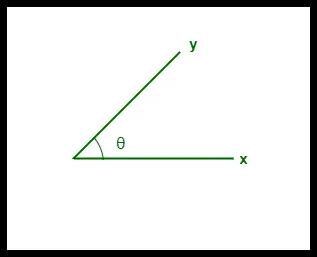
Cosinus Podobieństwo między dwoma wektorami
Zalety :
- Podobieństwo cosinus jest korzystne, ponieważ nawet jeśli dwa podobne obiekty danych są daleko od siebie o odległość euklidesową ze względu na rozmiar, nadal mogą mieć między sobą mniejszy kąt. Im mniejszy kąt, tym większe podobieństwo.
- Cosinus podobieństwa naniesiony na przestrzeń wielowymiarową odzwierciedla orientację (kąt) obiektów danych, a nie wielkość.