- DFA odnosi się do deterministycznych automatów skończonych. Determinizm odnosi się do niepowtarzalności obliczeń. Automaty skończone nazywane są deterministycznymi automatami skończonymi, jeśli maszyna czyta ciąg wejściowy po jednym symbolu na raz.
- W DFA istnieje tylko jedna ścieżka dla określonych danych wejściowych od bieżącego stanu do następnego stanu.
- DFA nie akceptuje ruchu zerowego, tj. DFA nie może zmienić stanu bez wprowadzenia znaku.
- DFA może zawierać wiele stanów końcowych. Jest używany w analizie leksykalnej w kompilatorze.
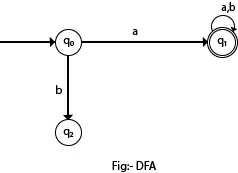
Na poniższym schemacie widać, że ze stanu q0 dla wejścia a istnieje tylko jedna ścieżka prowadząca do q1. Podobnie z q0 istnieje tylko jedna ścieżka wejścia b prowadząca do q2.
Formalna definicja DFA
DFA to zbiór 5 krotek, tak jak opisaliśmy w definicji FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Funkcję przejścia można zdefiniować jako:
δ: Q x ∑→Q
Graficzne przedstawienie DFA
DFA można przedstawić za pomocą dwuznaków zwanych diagramami stanu. W którym:
- Stan jest reprezentowany przez wierzchołki.
- Łuk oznaczony znakiem wejściowym pokazuje przejścia.
- Stan początkowy zaznaczony jest strzałką.
- Stan końcowy jest oznaczony podwójnym kółkiem.
Przykład 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Rozwiązanie:
Schemat przejścia:

Tabela przejściowa:
| Stan obecny | Następny stan dla wejścia 0 | Następny stan wejścia 1 |
|---|---|---|
| →q0 | q0 | pytanie 1 |
| pytanie 1 | q2 | pytanie 1 |
| *q2 | q2 | q2 |
Przykład 2:
DFA z ∑ = {0, 1} akceptuje wszystkie zaczynające się od 0.
Java równa się metoda
Rozwiązanie:

Wyjaśnienie:
- Na powyższym schemacie widzimy, że po podaniu 0 jako wejścia do DFA w stanie q0, DFA zmienia stan na q1 i zawsze przechodzi do stanu końcowego q1 na wejściu startowym 0. Może przyjąć 00, 01, 000, 001... .itp. Nie może zaakceptować żadnego łańcucha zaczynającego się od 1, ponieważ nigdy nie przejdzie do stanu końcowego w łańcuchu zaczynającym się od 1.
Przykład 3:
DFA z ∑ = {0, 1} akceptuje wszystkie kończące się na 0.
Rozwiązanie:

Wyjaśnienie:
Na powyższym schemacie widać, że przy danym 0 jako wejściu do DFA w stanie q0, DFA zmienia stan na q1. Może zaakceptować dowolny ciąg znaków kończący się na 0, np. 00, 10, 110, 100… itd. Nie może zaakceptować żadnego łańcucha zakończonego na 1, ponieważ nigdy nie przejdzie do stanu końcowego q1 na wejściu 1, więc ciąg kończący się na 1 nie zostanie zaakceptowany lub zostanie odrzucony.
