Sortowanie przez wstawianie i sortowanie przez wybór to dwa popularne algorytmy sortowania, a główna różnica między nimi polega na sposobie wybierania i umieszczania elementów w posortowanej kolejności.
Sortowanie przez wybór:
- Podczas sortowania przez wybór tablica wejściowa jest dzielona na dwie części: część posortowaną i część nieposortowaną.
- Algorytm wielokrotnie znajduje element minimalny w nieposortowanej części i zamienia go z skrajnie lewym elementem nieposortowanej części, rozszerzając w ten sposób posortowaną część o jeden element.
- Sortowanie przez wybór ma we wszystkich przypadkach złożoność czasową O(n^2).
Sortowanie przez wstawianie:
- Podczas sortowania przez wstawianie tablica wejściowa jest również dzielona na dwie części: część posortowaną i część nieposortowaną.
Algorytm pobiera element z nieposortowanej części i umieszcza go we właściwej pozycji w posortowanej części, przesuwając większe elementy o jedną pozycję w prawo.
Sortowanie przez wstawianie ma w najgorszym przypadku złożoność czasową O(n^2), ale może działać lepiej w przypadku tablic częściowo posortowanych, w najlepszym przypadku złożoność czasowa O(n).
Główne różnice: - Sortowanie przez wybór skanuje nieposortowaną część w celu znalezienia minimalnego elementu, natomiast sortowanie przez wstawianie skanuje posortowaną część w celu znalezienia właściwej pozycji do umieszczenia elementu.
Sortowanie przez wybór wymaga mniej zamian niż sortowanie przez wstawianie, ale za to więcej porównań.
Sortowanie przez wstawianie jest bardziej wydajne niż sortowanie przez wybór, gdy tablica wejściowa jest posortowana częściowo lub prawie posortowana, natomiast sortowanie przez wybieranie działa lepiej, gdy tablica jest w dużym stopniu nieposortowana.
Podsumowując, oba algorytmy mają podobną złożoność czasową, ale różnią się metody ich selekcji i rozmieszczania. Wybór między nimi zależy od charakterystyki danych wejściowych i specyficznych wymagań rozpatrywanego problemu.
Zalety sortowania przez wstawianie:
- Proste i łatwe do zrozumienia i wdrożenia.
- Wydajne w przypadku małych zestawów danych lub prawie posortowanych danych.
- Algorytm sortowania na miejscu, co oznacza, że nie wymaga dodatkowej pamięci.
- Stabilny algorytm sortowania, co oznacza, że utrzymuje względną kolejność równych elementów w tablicy wejściowej.
Wady sortowania przez wstawianie:
- Nieefektywne w przypadku dużych zestawów danych lub danych o odwrotnej kolejności, z złożonością czasową w najgorszym przypadku O(n^2).
- Sortowanie przez wstawianie zawiera wiele zamian, co może spowalniać działanie na nowoczesnych komputerach.
Zalety sortowania przez wybór:
- Proste i łatwe do zrozumienia i wdrożenia.
- Wydajne w przypadku małych zestawów danych lub prawie posortowanych danych.
- Algorytm sortowania na miejscu, co oznacza, że nie wymaga dodatkowej pamięci.
Wady sortowania przez wybór:
- Nieefektywne w przypadku dużych zbiorów danych, w najgorszym przypadku złożoność czasowa O(n^2).
- Sortowanie przez wybór zawiera wiele porównań, co może spowolnić działanie na nowoczesnych komputerach.
- Niestabilny algorytm sortowania, co oznacza, że może nie zachować względnej kolejności równych elementów w tablicy wejściowej.
W tym artykule omówimy różnicę między sortowaniem przez wstawianie a sortowaniem przez wybór:
Sortowanie przez wstawianie to prosty algorytm sortowania, który działa podobnie do sposobu sortowania kart do gry, które masz na rękach. Tablica jest praktycznie podzielona na część posortowaną i nieposortowaną. Wartości z nieposortowanej części są wybierane i umieszczane we właściwym miejscu w posortowanej części.
Algorytm:
Aby posortować tablicę o rozmiarze n w kolejności rosnącej:
- Wykonaj iterację od arr[1] do arr[n] po tablicy.
- Porównaj bieżący element (klucz) z jego poprzednikiem.
- Jeśli kluczowy element jest mniejszy niż jego poprzednik, porównaj go z elementami wcześniejszymi. Przesuń większe elementy o jedną pozycję w górę, aby zrobić miejsce na zamieniony element.
Poniżej znajduje się obraz ilustrujący sortowanie przez wstawianie:
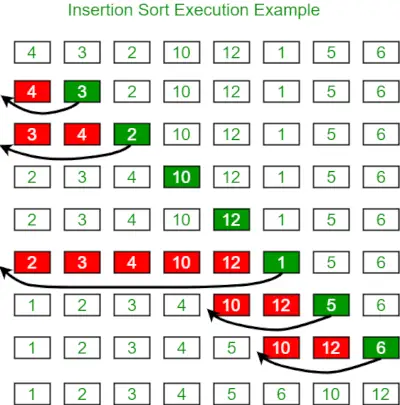
Poniżej znajduje się program do tego samego:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> klucz) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = klucz; } } // Funkcja wyświetlająca tablicę o rozmiarze N void printArray(int arr[], int n) { int i; // Wydrukuj tablicę dla (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Jawa
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> klucz) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = klucz; } } // Funkcja wyświetlająca tablicę o rozmiarze N static void printArray(int arr[], int n) { int i; // Wydrukuj tablicę dla (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Kod sterownika public static void main(String[ ] argumenty) { int arr[] = { 12, 11, 13, 5, 6 }; int N = długość tablicy; // Wywołanie funkcji wstawianieSort(arr, N); printArray(arr, N); Ten kod jest udostępniany przez code_hunt |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>=>0>and>arr[j]>klucz):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> klucz) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = klucz; } } // Funkcja wyświetlająca tablicę o rozmiarze N static void printArray(int[] arr, int n) { int i; // Wydrukuj tablicę dla (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Kod sterownika static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 } int N = arr.Length; // Wywołanie funkcji wstawianieSort(arr, N); printArray(arr, N) } // Ten kod to wniesiony przez Dharanendrę L V>>>JavaScript
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> klucz) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = klucz; } } // Funkcja wyświetlająca tablicę o rozmiarze N funkcja printArray(arr,n) { let i; // Wydrukuj tablicę dla (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Kod sterownika let arr=[12, 11 , 13, 5, 6]; niech N = arr.length; // Wywołanie funkcji wstawianieSort(arr, N); printArray(arr, N); // Ten kod został napisany przez avanitrachhadiya2155>>>Wyjście:5 6 11 12 13>The sortowanie przez wybór algorytm sortuje tablicę, wielokrotnie znajdując minimalny element (biorąc pod uwagę kolejność rosnącą) z nieposortowanej części i umieszczając go na początku. Algorytm utrzymuje dwie podtablice w danej tablicy.
- Podtablica jest już posortowana.
- Pozostała podtablica jest nieposortowana.
W każdej iteracji sortowania przez wybór wybierany jest minimalny element (biorąc pod uwagę porządek rosnący) z nieposortowanej podtablicy i przenoszony do posortowanej podtablicy.
Poniżej znajduje się przykład wyjaśniający powyższe kroki:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Poniżej znajduje się program do tego samego:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Jawa
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
wiek Ankity Lokhande
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>JavaScript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Wyjście:Sorted array: 11 12 22 25 64>Tabelaryczna różnica między sortowaniem przez wstawianie a sortowaniem przez wybór:
Sortowanie przez wstawianie Sortowanie przez wybór 1. Wstawia wartość do wstępnie posortowanej tablicy, aby posortować zestaw wartości w tablicy. Znajduje minimalną/maksymalną liczbę z listy i sortuje ją w kolejności rosnącej/malejącej. 2. Jest to stabilny algorytm sortowania. Jest to niestabilny algorytm sortowania. 3. W najlepszym przypadku złożoność czasowa wynosi Ω(N), gdy tablica jest już w porządku rosnącym. Ma Θ(N2) w najgorszym i średnim przypadku. W przypadku najlepszego, najgorszego przypadku i średniego sortowania przez selekcję mają złożoność Θ(N2). 4. Liczba operacji porównania wykonanych w tym algorytmie sortowania jest mniejsza niż wykonana zamiana. Liczba operacji porównania wykonanych w tym algorytmie sortowania jest większa niż wykonana zamiana. 5. Jest bardziej efektywny niż sortowanie przez Wybór. Jest mniej wydajny niż sortowanie przez wstawianie. 6. Tutaj element jest już znany i szukamy odpowiedniego miejsca na jego umieszczenie. Miejsce umieszczenia elementu jest już znane, szukamy elementu, który można wstawić w tym miejscu. 7. Sortowanie przez wstawianie stosuje się, gdy:
- Tablica ma niewielką liczbę elementów
- Do uporządkowania pozostało już tylko kilka elementów
Sortowanie przez wybór jest używane, gdy
- Mała lista ma zostać posortowana
- Koszt wymiany nie ma znaczenia
- Sprawdzenie wszystkich elementów jest obowiązkowe
- Koszt zapisu do pamięci ma znaczenie jak w pamięci flash (liczba zamian to O(n) w porównaniu do O(n2) w przypadku sortowania bąbelkowego)
8. Sortowanie przez wstawianie jest adaptacyjne, tj. efektywne w przypadku zbiorów danych, które są już zasadniczo posortowane: złożoność czasowa wynosi O(kn) gdy każdy element na wejściu jest nie większy niż k miejsca oddalone od posortowanej pozycji Sortowanie przez wybór to lokalny algorytm sortowania porównawczego
