Ścieżka Eulera to ścieżka w grafie, która odwiedza każdą krawędź dokładnie raz. Obwód Eulera to ścieżka Eulera, która zaczyna się i kończy w tym samym wierzchołku.
jak zdobyć gołębia łownego na Androida


Jak sprawdzić, czy dany graf jest eulerowski czy nie?
Problem jest taki sam, jak w następującym pytaniu. Czy można narysować dany wykres bez odrywania ołówka od papieru i bez przerysowywania którejkolwiek krawędzi więcej niż raz?
Graf nazywa się Eulerowskim, jeśli ma cykl Eulera, i Semi-Eulerowskim, jeśli ma ścieżkę Eulera. Problem wydaje się podobny do ścieżki Hamiltona, która jest problemem NP zupełnym dla grafu ogólnego. Na szczęście w czasie wielomianowym możemy stwierdzić, czy dany graf ma ścieżkę Eulera, czy nie. W rzeczywistości możemy to znaleźć w czasie O(V+E).
Poniżej przedstawiono kilka interesujących właściwości grafów nieskierowanych ze ścieżką i cyklem Eulera. Możemy użyć tych właściwości, aby sprawdzić, czy graf jest Eulerowski, czy nie.
Cykl Eulera: Graf nieskierowany ma cykl Eulera, jeśli spełnione są dwa poniższe warunki.
- Wszystkie wierzchołki o stopniu niezerowym są połączone. Nie interesują nas wierzchołki o stopniu zerowym, ponieważ nie należą one do cyklu lub ścieżki Eulera (bierzemy pod uwagę tylko wszystkie krawędzie).
- Wszystkie wierzchołki mają stopień parzysty.
Ścieżka Eulera: Graf nieskierowany ma ścieżkę Eulera, jeśli spełnione są dwa poniższe warunki.
- Taki sam jak warunek (a) dla cyklu Eulera.
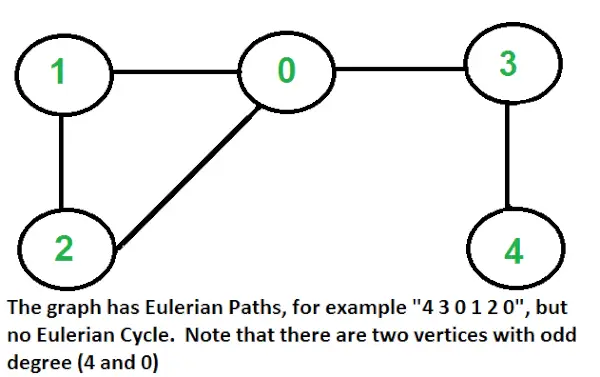
- Jeśli zero lub dwa wierzchołki mają stopień nieparzysty, a wszystkie pozostałe wierzchołki mają stopień parzysty. Należy pamiętać, że w grafie nieskierowanym nie jest możliwy tylko jeden wierzchołek o stopniu nieparzystym (w grafie nieskierowanym suma wszystkich stopni jest zawsze parzysta)
Należy zauważyć, że graf bez krawędzi jest uważany za eulerowski, ponieważ nie ma krawędzi, które można przejść.
Jak to działa?
Na ścieżce Eulera za każdym razem, gdy odwiedzamy wierzchołek v, przechodzimy przez dwie nieodwiedzone krawędzie z jednym punktem końcowym jako v. Dlatego wszystkie środkowe wierzchołki na ścieżce Eulera muszą mieć parzysty stopień. W przypadku cyklu Eulera dowolny wierzchołek może być wierzchołkiem środkowym, dlatego wszystkie wierzchołki muszą mieć stopień parzysty.
Realizacja:
C++
// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> >int> V;>// No. of vertices> >list<>int>>*przym;>// A dynamic array of adjacency lists> public>:> >// Constructor and destructor> >Graph(>int> V) {>this>->V = V; przym =>new> list<>int>>[W]; }> >~Graph() {>delete> [] adj; }>// To avoid memory leak> >// function to add an edge to graph> >void> addEdge(>int> v,>int> w);> >// Method to check if this graph is Eulerian or not> >int> isEulerian();> >// Method to check if all non-zero degree vertices are connected> >bool> isConnected();> >// Function to do DFS starting from v. Used in isConnected();> >void> DFSUtil(>int> v,>bool> visited[]);> };> void> Graph::addEdge(>int> v,>int> w)> {> >adj[v].push_back(w);> >adj[w].push_back(v);>// Note: the graph is undirected> }> void> Graph::DFSUtil(>int> v,>bool> visited[])> {> >// Mark the current node as visited and print it> >visited[v] =>true>;> >// Recur for all the vertices adjacent to this vertex> >list<>int>>::iterator i;> >for> (i = adj[v].begin(); i != adj[v].end(); ++i)> >if> (!visited[*i])> >DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> >// Mark all the vertices as not visited> >bool> visited[V];> >int> i;> >for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) zwróć fałsz; zwróć wartość true; } /* Funkcja zwraca jedną z następujących wartości 0 --> Jeśli graf nie jest Eulerowski 1 --> Jeśli graf ma ścieżkę Eulera (semi-eulerowską) 2 --> Jeśli graf ma obwód Eulera (Eulerowski) */ int Graph::isEulerian() { // Sprawdź, czy wszystkie wierzchołki stopnia niezerowego są połączone if (isConnected() == false) return 0; // Zliczanie wierzchołków o stopniu nieparzystym int nieparzysty = 0; for (int i = 0; i if (adj[i].size() & 1) odd++; // Jeśli liczba jest większa niż 2, to wykres nie jest Eulerowski if (nieparzysty> 2) return 0; // Jeśli jest nieparzysty liczba wynosi 2, a następnie jest semi-eulerowska. // Jeśli liczba nieparzysta wynosi 0, wówczas liczba nieparzysta nigdy nie może wynosić 1 w przypadku nieskierowanego wykresu (nieparzystego)? } // Funkcja do uruchamiania przypadków testowych void test(Wykres &g) { int res = g.isEulerian(); if (res == 0) cout<< 'graph is not Eulerian
'; else if (res == 1) cout << 'graph has a Euler path
'; else cout << 'graph has a Euler cycle
'; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }> |
>
>
Jawa
// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> >private> int> V;>// No. of vertices> >// Array of lists for Adjacency List Representation> >private> LinkedList adj[];> >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> LinkedList[v];> >for> (>int> i=>0>; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) zwróć fałsz; zwróć wartość true; } /* Funkcja zwraca jedną z następujących wartości 0 --> Jeśli graf nie jest Eulerowski 1 --> Jeśli graf ma ścieżkę Eulera (semi-eulerowską) 2 --> Jeśli graf ma obwód Eulera (Eulerowski) */ int isEulerian() { // Sprawdź, czy wszystkie wierzchołki stopnia niezerowego są połączone if (isConnected() == false) return 0; // Zliczanie wierzchołków o stopniu nieparzystym int nieparzysty = 0; for (int i = 0; i if (adj[i].size()%2!=0) odd++; // Jeśli liczba jest większa niż 2, to wykres nie jest Eulerowski jeśli (nieparzysty> 2) zwraca 0; / / Jeśli liczba nieparzysta wynosi 2, to semi-eulerian. // Jeśli liczba nieparzysta wynosi 0, to eulerian // Zauważ, że liczba nieparzysta nigdy nie może wynosić 1 w przypadku nieskierowanego zwrotu grafu (nieparzysty==2) 1 : 2; Funkcja do uruchamiania przypadków testowych void test() { int res = isEulerian(); if (res == 0) System.out.println('wykres nie jest Eulerowski' else if (res == 1) System. out.println('wykres ma ścieżkę Eulera'); else System.out.println('wykres ma cykl Eulera'); } // Metoda sterownika public static void main(String args[]) { / / Utwórzmy i przetestujmy wykresy pokazane na powyższych rysunkach Wykres g1 = nowy Graf(5); g1.addEdge(0, 2); g1.addEdge(2, 1); (0, 3); g1.addEdge(3, 4); g1.test(); Wykres g2 = nowy wykres(5); g2.addEdge(1, 0); addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(4, 0); g2.test(); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Stwórzmy graf z 3 wierzchołkami // połączonymi w formie cyklu Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Stwórzmy graf ze wszystkimi wierzchołkami // o stopniu zerowym Graph g5 = new Graph(3); g5.test(); } } // Ten kod został stworzony przez Aakash Hasija> |
>
>
Python3
# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections>import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> >def> __init__(>self>, vertices):> >self>.V>=> vertices># No. of vertices> >self>.graph>=> defaultdict(>list>)># default dictionary to store graph> ># function to add an edge to graph> >def> addEdge(>self>, u, v):> >self>.graph[u].append(v)> >self>.graph[v].append(u)> ># A function used by isConnected> >def> DFSUtil(>self>, v, visited):> ># Mark the current node as visited> >visited[v]>=> True> ># Recur for all the vertices adjacent to this vertex> >for> i>in> self>.graph[v]:> >if> visited[i]>=>=> False>:> >self>.DFSUtil(i, visited)> >'''Method to check if all non-zero degree vertices are> >connected. It mainly does DFS traversal starting from> >node with non-zero degree'''> >def> isConnected(>self>):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.V)> ># Find a vertex with non-zero degree> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i]) !>=> 0>:> >break> ># If there are no edges in the graph, return true> >if> i>=>=> self>.V>->1>:> >return> True> ># Start DFS traversal from a vertex with non-zero degree> >self>.DFSUtil(i, visited)> ># Check if all non-zero degree vertices are visited> >for> i>in> range>(>self>.V):> >if> visited[i]>=>=> False> and> len>(>self>.graph[i])>>0>:> >return> False> >return> True> >'''The function returns one of the following values> >0 -->Jeśli graf nie jest Eulerowski> >1 -->Jeśli graf ma ścieżkę Eulera (semi-eulerowską)> >2 -->Jeśli graf ma obwód Eulera (Eulerian) '''> >def> isEulerian(>self>):> ># Check if all non-zero degree vertices are connected> >if> self>.isConnected()>=>=> False>:> >return> 0> >else>:> ># Count vertices with odd degree> >odd>=> 0> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i])>%> 2> !>=> 0>:> >odd>+>=> 1> >'''If odd count is 2, then semi-eulerian.> >If odd count is 0, then eulerian> >If count is more than 2, then graph is not Eulerian> >Note that odd count can never be 1 for undirected graph'''> >if> odd>=>=> 0>:> >return> 2> >elif> odd>=>=> 2>:> >return> 1> >elif> odd>>2>:> >return> 0> ># Function to run test cases> >def> test(>self>):> >res>=> self>.isEulerian()> >if> res>=>=> 0>:> >print>(>'graph is not Eulerian'>)> >elif> res>=>=> 1>:> >print>(>'graph has a Euler path'>)> >else>:> >print>(>'graph has a Euler cycle'>)> # Let us create and test graphs shown in above figures> g1>=> Graph(>5>)> g1.addEdge(>1>,>0>)> g1.addEdge(>0>,>2>)> g1.addEdge(>2>,>1>)> g1.addEdge(>0>,>3>)> g1.addEdge(>3>,>4>)> g1.test()> g2>=> Graph(>5>)> g2.addEdge(>1>,>0>)> g2.addEdge(>0>,>2>)> g2.addEdge(>2>,>1>)> g2.addEdge(>0>,>3>)> g2.addEdge(>3>,>4>)> g2.addEdge(>4>,>0>)> g2.test()> g3>=> Graph(>5>)> g3.addEdge(>1>,>0>)> g3.addEdge(>0>,>2>)> g3.addEdge(>2>,>1>)> g3.addEdge(>0>,>3>)> g3.addEdge(>3>,>4>)> g3.addEdge(>1>,>3>)> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4>=> Graph(>3>)> g4.addEdge(>0>,>1>)> g4.addEdge(>1>,>2>)> g4.addEdge(>2>,>0>)> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5>=> Graph(>3>)> g5.test()> # This code is contributed by Neelam Yadav> |
>
>
ridhima tiwari
C#
// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> >private> int> V;>// No. of vertices> > >// Array of lists for Adjacency List Representation> >private> List<>int>>[]przym;> > >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> List<>int>>[w];> >for> (>int> i=0; i adj[i] = new List |
>
>
JavaScript
> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> >// Constructor> >constructor(v)> >{> >this>.V = v;> >this>.adj =>new> Array(v);> >for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i |
>
>Wyjście
graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle>
Złożoność czasowa: O(V+E)
Złożoność przestrzenna: O(V+E)
Następne artykuły:
Ścieżka i obwód Eulera dla grafów skierowanych.
Algorytm Fleury’ego do wydrukowania ścieżki lub obwodu Eulera?
