W tym artykule omówimy multiplekser, najpierw zdefiniujemy, czym jest multiplekser, następnie przejdziemy przez jego typy, którymi są 2×1 i 4×1, a następnie przejdziemy przez implementację multipleksera 2×1 i wyższych multiplekser z multiplekserem niższego rzędu. W końcu zakończymy nasz artykuł kilkoma zastosowaniami, zaletami i kilkoma często zadawanymi pytaniami.

Spis treści

• Czym są multipleksery?
• Rodzaje Muxów
• Multiplekser 2×1
• Multiplekser 4×1
• Implementacja różnych bramek z multiplekserem 2:1
• Implementacja MUX wyższego rzędu przy użyciu MUX niższego rzędu
• Zalety i wady MUX-a

Czym są multipleksery?

Multiplekser to m.in obwód kombinacyjny który ma wiele wejść danych i jedno wyjście, w zależności od wejść sterujących lub wybierających. Dla N linii wejściowych wymagane są linie wyboru log2(N) lub równoważnie2^nlinii wejściowych, potrzebnych jest n linii wyboru. Multipleksery są również znane jako selektory N do 1, konwertery równoległe na szeregowe, obwody wiele do jednego i uniwersalne obwody logiczne. Stosowane są głównie w celu zwiększenia ilości danych, które można przesłać siecią w określonym czasie oraz przepustowość łącza .

Multiplekser

Rodzaje Muxów

Mux może być różnych typów w zależności od danych wejściowych, ale w tym artykule omówimy dwa główne typy multiplekserów

• 2×1 Muks
• Mukser 4×1
  

Multiplekser 2×1

2×1 to podstawowy obwód, znany również jako multiplekser 2 do 1, który służy do wyboru jednego sygnał z dwóch wejść i przekazuje je na wyjście. Multiplekser 2×1 ma dwie linie wejściowe, jedną linię wyjściową i jedną linię wyboru. Ma różne zastosowania w systemach cyfrowych, np. w mikroprocesorze, służy do wyboru pomiędzy dwoma różnymi źródłami danych lub pomiędzy dwoma różnymi instrukcjami.

Schemat blokowy multipleksera 2:1 z tablicą prawdy

Poniżej znajduje się schemat blokowy i tabela prawdy 2:1 Mux. Na tym schemacie blokowym, gdzie I0 i I1 są liniami wejściowymi, Y jest linią wyjściową, a S0 jest pojedynczą linią wyboru.

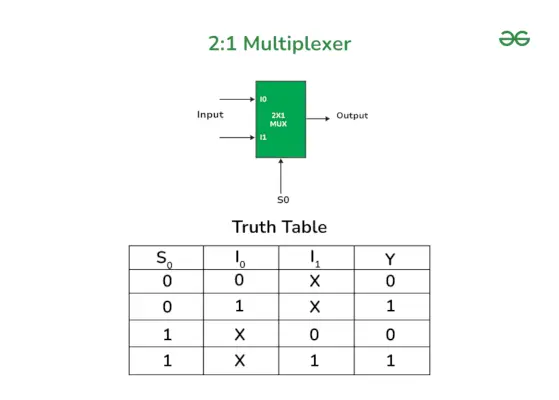
Schemat blokowy multipleksera 2:1 z tablicą prawdy

Wyjście multipleksera 2×1 będzie zależeć od linii wyboru S0,

• Gdy S wynosi 0 (niski), wybierane jest I0
• gdy S0 ma wartość 1 (wysoki), wybierane jest I1

Logiczne wyrażenie 2×1 Mux

Korzystając z tabeli prawdy, wyrażenie logiczne dla Mux można określić jako

Y=overline{S_0}.I_0+S_0.I_1

Schemat obwodu multiplekserów 2×1

Korzystanie z tabeli prawdy okrążenie schemat można podać jako

Schemat obwodu multipleksera 2×1

Multiplekser 4×1

Multiplekser 4×1, znany również jako multiplekser 4 do 1. Jest to multiplekser posiadający 4 wejścia i jedno wyjście. Wyjście jest wybierane jako jedno z 4 wejść w oparciu o wybór wejść. Liczba linii wyboru będzie zależała od numeru wejścia określonego przez równanielog_2n,W 4×1 Mux linie wyboru można określić jakolog_4=2,slo potrzebne są dwie selekcje.

Schemat blokowy multipleksera 4×1

Na podanym schemacie blokowym I0, I1, I2 i I3 to 4 wejścia, a Y to pojedyncze wyjście oparte na liniach Select S0 i S1.

Sygnał wyjściowy multipleksera jest określony przez wartość binarną linii wyboru

• Gdy S1S0=00, wybrane jest wejście I0.
• Gdy S1S0=01, wybrane jest wejście I1.
• Gdy S1S0=10, wybrane jest wejście I2.
• Gdy S1S0=11, wybrane jest wejście I3.

Tabela prawdy multipleksera 4 × 1

Poniżej podano Tabela prawdy multipleksera 4×1

co jest w przypadku sql

Schemat obwodu multiplekserów 4×1

Korzystając z tabeli prawdy, schemat obwodu można podać jako

Multiplekser może pełnić funkcję uniwersalnego układu kombinacyjnego. Za pomocą multiplekserów można zrealizować wszystkie standardowe bramki logiczne.

obsada sql

Implementacja różnych bramek z multiplekserem 2:1

Poniżej podano implementację innej bramki przy użyciu multipleksera 2:1

Implementacja bramki NOT przy użyciu multipleksera 2:1

Bramkę Not z 2:1 Mux można uzyskać poprzez

• Podłącz sygnał wejściowy do jednej z linii wejściowych danych (I0).
• Następnie podłącz linię (0 lub 1) do drugiej linii wejściowej danych (I1)
• Podłącz tę samą linię wejściową. Wybierz linię S0, która jest podłączona do D0.

Poniżej znajduje się diagram logicznej reprezentacji NIE brama przy użyciu multipleksera 2:1

Implementacja bramki AND przy użyciu multipleksera 2:1

Bramę And z 2:1 Mux można uzyskać poprzez

• Podłącz wejście Y do I1.
• Podłącz wejście X do linii wyboru S0.
• Podłącz linię (0) do I0.

Poniżej znajduje się diagram logicznej reprezentacji ORAZ brama przy użyciu multipleksera 2:1

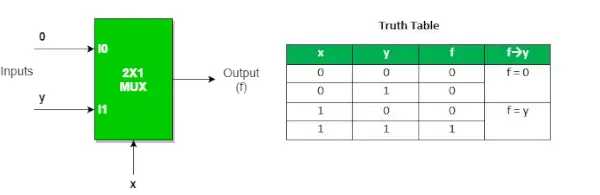
Więcej informacji na temat Implementacja bramki AND przy użyciu multipleksera 2:1

Implementacja bramki OR przy użyciu multipleksera 2:1

Bramkę OR z 2:1 Mux można uzyskać poprzez

• Podłącz wejście X do linii wyboru S0.
• Podłącz wejście Y do I1.
• Podłącz linię (1) do I1.

Poniżej znajduje się diagram logicznej reprezentacji LUB brama przy użyciu multipleksera 2:1

Implementacja bramek NAND, NOR, XOR i XNOR wymaga dwóch multiplekserów 2:1. Pierwszy multiplekser będzie działał jako bramka NOT, która zapewni uzupełnienie sygnału wejściowego do drugiego multipleksera.

Implementacja bramki NAND przy użyciu multipleksera 2:1

Bramkę NAND z 2:1 Mux można uzyskać poprzez

• W pierwszym multiplekserze przyjmujemy wejścia oraz 1, 0 i y jako linię wyboru.
• W drugim MUX-ie wyjście z multipleksera jest podłączone do I1.
• linia (1) jest podawana do I0.
• x jest podane jako linia wyboru dla drugiego Muxa.

Poniżej znajduje się diagram logicznej reprezentacji bramka NAND przy użyciu multipleksera 2:1

Więcej informacji na temat Implementacja bramki NAND przy użyciu multipleksera 2:1

Implementacja bramki NOR przy użyciu multipleksera 2:1

Bramę Nor z 2:1 Mux można zdobyć poprzez

• W pierwszym multiplekserze przyjmujemy wejścia oraz 1, 0 i y jako linię wyboru.
• W drugim MUX-ie wyjście z multipleksera jest podłączone do I0.
• linia (0) jest podawana do I1.
• x jest podane jako linia wyboru dla drugiego Muxa.

Poniżej znajduje się diagram logicznej reprezentacji bramka NOR przy użyciu multipleksera 2:1

Więcej informacji na temat Implementacja bramki NOR przy użyciu multipleksera 2:1

Implementacja bramki EX-OR z wykorzystaniem multipleksera 2:1

Bramę Nor z 2:1 Mux można zdobyć poprzez

• W pierwszym multiplekserze przyjmujemy wejścia oraz 1, 0 i y jako linię wyboru.
• W drugim MUX-ie wyjście z multipleksera jest podłączone do I1.
• y jest podawane do I0.
• x jest podane jako linia wyboru dla drugiego Muxa.

Poniżej znajduje się diagram logicznej reprezentacji Brama EX-OR przy użyciu multipleksera 2:1

Implementacja bramki EX-NOR z wykorzystaniem multipleksera 2:1

Poniżej znajduje się diagram logicznej reprezentacji Brama EX-OR przy użyciu multipleksera 2:1

Bramę Nor z 2:1 Mux można zdobyć poprzez

• W pierwszym multiplekserze przyjmujemy wejścia oraz 1, 0 i y jako linię wyboru.
• W drugim MUX-ie wyjście z multipleksera jest podłączone do I0.
• y jest podawane do I1.
• x jest podane jako linia wyboru dla drugiego Muxa.

Implementacja MUX wyższego rzędu przy użyciu MUX niższego rzędu

Poniżej podano implementację MUX wyższego rzędu przy użyciu MUX niższego rzędu

4:1 MUX przy użyciu 2:1 MUX

Do wdrożenia 4:1 MUX wymagane są trzy MUX 2:1.

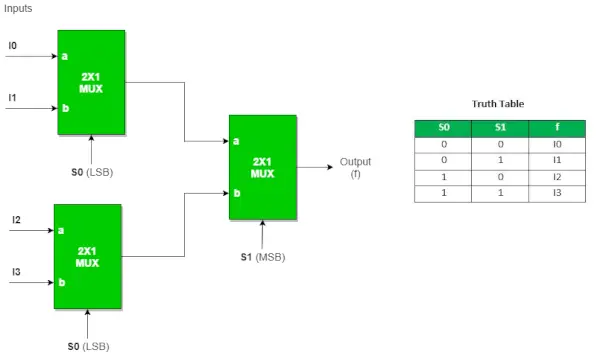
Podobnie,

Podczas gdy MUX 8:1 wymaga siedmiu (7) MUX 2:1, MUX 16:1 wymaga piętnastu (15) MUX 2:1, a MUX 64:1 wymaga sześćdziesięciu trzech (63) MUX 2:1. Możemy zatem wyciągnąć wniosek, że A2^n:1MUX wymaga(2^n-1) 2:1 MUXes.

16:1 MUX przy użyciu 4:1 MUX

Poniżej znajduje się logiczny diagram multipleksera 16:1 przy użyciu multipleksera 4:1

Ogólnie rzecz biorąc, aby zaimplementować B: 1 MUX przy użyciu A: 1 MUX, do zaimplementowania tego samego używa się jednej formuły.
B / A = K1,
K1/A = K2,
K2/A = K3

K_N-1/ A = K_N= 1 (aż otrzymamy 1 liczbę MUX).

A następnie dodaj wszystkie liczby MUX-ów = K1 + K2 + K3 +…. + K_N.
Aby zaimplementować MUX 64:1 przy użyciu MUX 4:1
Korzystając z powyższego wzoru, możemy otrzymać to samo.
64/4 = 16
16/4 = 4
4/4 = 1 (aż otrzymamy 1 liczbę MUX)
Zatem do zaimplementowania 64:1 MUX = 16 + 4 + 1 = 21 wymagana jest całkowita liczba MUX 4:1.

fa ( A, B, C) =sum( 1, 2, 3, 5, 6 ) z „nie obchodzi mnie to” (7)

używając A i B jako linii wyboru dla MUX 4:1,

AB jako wybrane: Rozszerzenie terminów minterms do postaci logicznej i zobaczenie ich wartości 0 lub 1 na miejscu C, dzięki czemu można je umieścić w ten sposób.

AC jako wybrane : Rozszerzenie terminów minterms do ich postaci logicznej i zobaczenie ich wartości 0 lub 1 na B-tym miejscu, aby można je było umieścić w ten sposób.

k algorytm grupowania

BC jako wybrane : Rozszerzanie Mintermy do swojej postaci logicznej i zobaczy jej wartość 0 lub 1 w A^tmiejsce, aby można je było umieścić w ten sposób.

Zalety i wady MUX-a

Poniżej przedstawiono zalety i wady MUX

Zalety MUX-a

Poniżej podano zalety MUX

• Efektywność : Mux ma dobrą skuteczność w kierowaniu wielu sygnałów wejściowych do pojedynczego sygnału wyjściowego w oparciu o sygnały sterujące.
• Optymalizacja : Mux pomaga oszczędzać zasoby, takie jak przewody, szpilki i układ scalony (IC).
• Różne wdrożenia: Mux może być używany do implementowania różnych cyfrowych funkcji logicznych, takich jak AND, OR itp.
• Elastyczność: Mux można łatwo skonfigurować zgodnie z wymaganiami i dostosować do różnych źródeł danych, zwiększając wszechstronność systemu.

Wady MUX-a

Poniżej podano wady MUX

• Ograniczona liczba źródeł danych: Liczba sygnałów wejściowych, które może przyjąć multiplekser, jest ograniczona liczbą linii sterujących, co może powodować ograniczenia w niektórych zastosowaniach.
• Opóźnienie: Multipleksery mogą mieć pewne opóźnienia w ścieżce sygnału, co może mieć wpływ na wydajność obwodu.
• Złożone uzasadnienie kontroli: Logika sterowania multiplekserów może być złożona, szczególnie w przypadku większych multiplekserów z dużą liczbą wejść.
• Zużycie energii: Multipleksery mogą zużywać więcej energii w porównaniu z innymi prostymi l brama ogiczna , zwłaszcza gdy mają dużą liczbę wejść.

Zastosowania MUX-a

Poniżej podano zastosowania MUX

• Trasowanie danych : Mux służy do trasowania danych w systemie cyfrowym, gdzie wybierają jedną z kilku linii danych i przekierowują ją na wyjście.
• Wybór danych : Mux służy do selekcji danych, gdzie wybierają źródło danych zgodnie z liniami wyboru.
• Konwersja analogowo-cyfrowa : Mux są używane w ADC aby wybrać różne analogowe kanały wejściowe.
• Dekodowanie adresu : Mux są używane w Mikroprocesory lub pamięć do dekodowania adresu.
• Implementacja funkcji logicznej : Muxy mogą być użyte do realizacji różnych funkcji logicznych.

Wniosek

W tym artykule omówiliśmy MUX, widzieliśmy różne typy multiplekserów, którymi są multipleksery 2×1 i 4×1, przeszliśmy przez implementację multipleksera 2×1 i wyższego multipleksu z multiplekserem niższego rzędu. Omówiliśmy także w skrócie jego zalety, wady i zastosowania.

Multipleksery w logice cyfrowej – często zadawane pytania

Dlaczego logika sterowania multiplekserów jest uważana za złożoną?

Mux może być skomplikowany, zwłaszcza w przypadku większych multiplekserów ze względu na sygnały sterujące, które wybierają wejścia w oparciu o wymagania aplikacji.

Jakie są różne typy architektur multiplekserów?

Architektury multiplekserów zmieniają się w zależności od takich czynników, jak całkowita liczba wejść, liczba linii wyboru i logika używana do wyboru wejścia.

W jaki sposób multipleksery są wykorzystywane w aplikacjach cyfrowego przetwarzania sygnału (DSP)?

W zastosowaniach DSP multipleksery służą do kierowania, selekcji i przetwarzania sygnału.