Bramki logiczne są podstawowymi elementami wszystkich obwodów i systemów cyfrowych. W elektronice cyfrowej są siedem głównych typów bramek logicznych używany do wykonywania różnych operacji logicznych. Bramka logiczna to w zasadzie obwód elektroniczny zaprojektowany przy użyciu komponentów takich jak diody, tranzystory, rezystory, kondensatory itp. i zdolne do wykonywania operacji logicznych. W tym artykule przestudiujemy definicję, tabelę prawdy i inne powiązane koncepcje bramek logicznych. Zacznijmy więc od podstawowego wprowadzenia bramek logicznych.
Spis treści
- Co to jest bramka logiczna?
- Rodzaje bramek logicznych
- ORAZ Brama
- LUB Brama
- NIE Brama
- Brama NOR
- Brama NAND
- Brama XOR
- Brama XNOR
- Zastosowania bramek logicznych
Co to jest bramka logiczna?
A bramka logiczna to obwód elektroniczny zaprojektowany przy użyciu elementów elektronicznych, takich jak diody, tranzystory, rezystory i inne. Jak sama nazwa wskazuje, bramka logiczna jest przeznaczona do wykonywania operacji logicznych w systemach cyfrowych, takich jak komputery, systemy komunikacyjne itp.
Dlatego możemy powiedzieć, że elementami składowymi obwodu cyfrowego są bramki logiczne, które wykonują liczne operacje logiczne wymagane przez każdy obwód cyfrowy. Bramka logiczna może przyjmować dwa lub więcej wejść, ale generować tylko jedno wyjście. Wynik bramki logicznej zależy od kombinacji wejść i operacji logicznej wykonywanej przez bramkę logiczną.
Zastosowanie bramek logicznych Algebra Boole’a do wykonywania procesów logicznych. Bramki logiczne znajdują się w prawie każdym gadżecie cyfrowym, z którego korzystamy na co dzień. Bramki logiczne są stosowane w architekturze naszych telefonów, laptopów, tabletów i urządzeń pamięci.
Rodzaje bramek logicznych
Bramka logiczna to bramka cyfrowa umożliwiająca manipulowanie danymi. Bramki logiczne, użyj logiki, aby określić, czy przekazać sygnał. Bramki logiczne natomiast regulują przepływ informacji w oparciu o zbiór reguł.
Bramki logiczne można podzielić na następujące główne typy:
1. Podstawowe bramki logiczne
Istnieją trzy podstawowe bramki logiczne:
- ORAZ Brama
- LUB Brama
- NIE Brama
2. Uniwersalne bramki logiczne
W elektronice cyfrowej za uniwersalne bramki logiczne uważa się następujące dwie bramki logiczne:
- Brama NOR
- Brama NAND
3. Wyprowadzone bramki logiczne
Poniżej przedstawiono dwie pochodne bramki logiczne stosowane w systemach cyfrowych:
- Brama XOR
- Brama XNOR
Omówmy teraz szczegółowo każdy z tych typów bramek logicznych, jeden po drugim.
ORAZ Brama
W elektronice cyfrowej bramka AND jest jedną z podstawowych bramek logicznych, która wykonuje logiczne mnożenie zastosowanych do niej wejść. Generuje stan wysoki lub logiczny 1 tylko wtedy, gdy wszystkie przyłożone do niego wejścia mają stan wysoki lub logiczny 1. W przeciwnym razie wyjście bramki AND ma stan niski lub logiczne 0.
Właściwości bramki AND:
Poniżej przedstawiono dwie główne właściwości bramki AND:
- Bramka AND może przyjąć jednocześnie dwie lub więcej wartości wejściowych.
- Gdy wszystkie wejścia mają stan logiczny 1, wyjście tej bramki ma stan logiczny 1.
Działanie bramki AND opisuje się za pomocą wyrażenia matematycznego, zwanego wyrażeniem boolowskim bramki AND.
W przypadku bramki AND z dwoma wejściami wyrażenie logiczne jest określone wzorem:
Z = A.B
Gdzie A i B są wejściami bramki AND, natomiast Z oznacza wyjście bramki AND.
Możemy rozszerzyć to wyrażenie na dowolną liczbę zmiennych wejściowych, takich jak:
Z=A.B.C.D…
Tabela prawdy bramki AND:
Tabela prawdy dwuwejściowej bramki AND jest podana poniżej:
Wejście | Wyjście | |
|---|---|---|
A drzewo binarne a drzewo wyszukiwania binarnego | B | A I B |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Symbol bramki AND:
Symbol logiczny bramki AND z dwoma wejściami pokazano na poniższym rysunku.
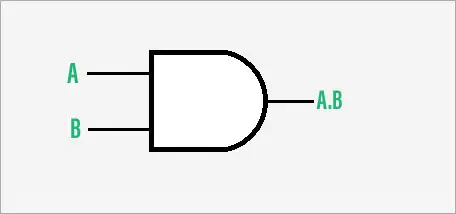
Symbol bramki dwuwejściowej AND
LUB Brama
W elektronice cyfrowej istnieje rodzaj podstawowej bramki logicznej, która wytwarza stan niski lub logiczne 0 tylko wtedy, gdy wszystkie jej wejścia mają stan niski lub logiczne 0. W przypadku wszystkich innych kombinacji wejść wyjście bramki OR ma stan wysoki lub logiczne 1. To bramka logiczna nazywana jest bramką OR. Bramkę OR można zaprojektować tak, aby miała dwa lub więcej wejść, ale tylko jedno wyjście. Podstawową funkcją bramki OR jest wykonywanie operacji na sumie logicznej.
Właściwości bramki OR:
Bramka OR ma dwie następujące właściwości:
- Może mieć dwie lub więcej linii wejściowych jednocześnie.
- Gdy wszystkie wejścia bramki OR mają stan niski lub logiczne 0, jej wyjście ma stan niski lub logiczne 0.
Działanie bramki OR można opisać matematycznie za pomocą wyrażenia matematycznego zwanego wyrażeniem boolowskim bramki OR.
Wyrażenie logiczne dla bramki OR z dwoma wejściami jest dane przez:
Z = A + B
Wyrażenie logiczne dla trójwejściowej bramki OR to:
Z = A + B + C
Tutaj A, B i C są danymi wejściowymi, a Z jest zmiennymi wyjściowymi. Możemy rozszerzyć to wyrażenie logiczne na dowolną liczbę zmiennych wejściowych.
Tabela prawdy bramki OR:
Tabela prawdy bramki OR opisuje relację między danymi wejściowymi i wyjściowymi. Poniżej znajduje się tabela prawdy dla dwuwejściowej bramki OR:
Wejście | Wyjście | |
|---|---|---|
A | B | A LUB B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Symbol bramki OR:
Symbol logiczny dwuwejściowej bramki OR pokazano na poniższym rysunku.

Symbol dwuwejściowej bramki OR
NIE Brama
W elektronice cyfrowej bramka NOT jest kolejną podstawową bramką logiczną wykorzystywaną do działania uzupełnienie sygnału wejściowego zastosował się do tego. Wymaga tylko jednego wejścia i jednego wyjścia. Wyjście bramki NOT jest uzupełnieniem zastosowanego do niej wejścia. Dlatego też, jeśli zastosujemy wyjście niskie lub logiczne 0 do bramki NOT, otrzymamy wyjście wysokie lub logiczne 1 i odwrotnie. Bramka NOT jest również nazywana falownikiem, ponieważ wykonuje operację inwersji.
Właściwości bramki NOT:
- Wyjście bramki NOT jest uzupełnieniem lub odwrotnością sygnału wejściowego zastosowanego do niej.
- Bramka NOT zajmuje tylko jedno wyjście.
Logiczne działanie bramki NOT opisane jest jej wyrażeniem boolowskim, które podano poniżej.
Z= overline{A}
Słupek nad zmienną wejściową A reprezentuje operację inwersji.
Tabela prawdy bramki OR:
Tabela prawdy opisuje relację między danymi wejściowymi i wyjściowymi. Poniżej znajduje się tabela prawdy dla bramki NOT:
Wejście | Wyjście |
|---|---|
A | ANI |
0 | 1 |
1 | 0 |
Symbol bramki NOT
Symbol obwodu logicznego bramki NOT pokazano na poniższym rysunku. Tutaj A jest linią wejściową, a Z jest linią wyjściową.

Symbol NIE Bramy
Brama NOR
Bramka NOR to rodzaj uniwersalnej bramki logicznej, która może przyjmować dwa lub więcej wejść, ale jedno wyjście. Jest to w zasadzie połączenie dwóch podstawowych bramek logicznych, tj. bramki OR i bramki NOT. Można to więc wyrazić następująco:
Brama NOR = bramka OR + bramka NOT
Innymi słowy, bramka NOR jest bramką OR, po której następuje bramka NOT.
Właściwości bramki NOR:
Poniżej przedstawiono dwie ważne właściwości bramki NOR:
logo javy
- Bramka NOR może mieć dwa lub więcej wejść i daje wyjście.
- Bramka NOR daje na wyjściu stan wysoki lub logiczną 1 tylko wtedy, gdy wszystkie jej wejścia są niskie lub logiczne 0.
Podobnie jak w przypadku podstawowych bramek logicznych, działanie bramki NOR możemy opisać za pomocą równania matematycznego zwanego wyrażeniem boolowskim bramki NOR.
Poniżej podano wyrażenie logiczne dwuwejściowej bramki NOR:
C=overline{A+B}
Możemy rozszerzyć to wyrażenie na dowolną liczbę zmiennych wejściowych.
W powyższych wyrażeniach boolowskich zmienne A i B nazywane są zmiennymi wejściowymi, natomiast zmienna C nazywana jest zmienną wyjściową.
Tabela prawdy bramy NOR:
Poniżej znajduje się tabela prawdy dwuwejściowej bramki NOR pokazująca związek między jej wejściami i wyjściami:
Wejście | Wyjście | |
|---|---|---|
A | B | A NOR B |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |

Symbol Bramy NOR
Brama NAND
W elektronice cyfrowej bramka NAND to kolejny rodzaj uniwersalnej bramki logicznej służącej do wykonywania operacji logicznych. Bramka NAND wykonuje odwrotną operację bramki AND. Podobnie jak bramka NOR, bramka NAND może mieć dwie lub więcej linii wejściowych, ale tylko jedną linię wyjściową.
Bramka NAND jest również reprezentowana jako kombinacja dwóch podstawowych bramek logicznych, a mianowicie bramki AND i bramki NOT. Dlatego można to wyrazić jako
Brama NAND = bramka AND + bramka NOT
Właściwości bramki NAND:
Poniżej przedstawiono dwie kluczowe właściwości bramki NAND:
algorytm Bellforda
- Bramka NAND może przyjmować jednocześnie dwa lub więcej wejść i wytwarzać jedno wyjście w oparciu o kombinację zastosowanych wejść.
- Bramka NAND generuje stan niski lub logiczny 0 tylko wtedy, gdy wszystkie jej wejścia są w stanie wysokim lub logicznym 1.
Wyrażenie bramki NAND możemy opisać za pomocą równania matematycznego zwanego wyrażeniem boolowskim. Oto wyrażenie logiczne dwuwejściowej bramki NAND.
C=overline{AB}
W tym wyrażeniu A i B są zmiennymi wejściowymi, a C jest zmienną wyjściową. Możemy rozszerzyć tę relację na dowolną liczbę zmiennych wejściowych, na przykład trzy, cztery lub więcej.
Tabela prawdy bramki NAND:
Tabela prawdy to tabela wejść i wyjść, która opisuje działanie bramki NAND i pokazuje logiczną zależność między nimi:
Wejście | Wyjście | |
|---|---|---|
A | B | NAND B |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Symbol bramki NAND:
Symbol logiczny bramki NAND jest reprezentowany jako bramka AND z bąbelkiem na końcu wyjściowym, jak pokazano na poniższym rysunku. Jest to symbol dwuwejściowej bramki NAND.

Symbol bramki NAND
Brama XOR
W elektronice cyfrowej istnieje specjalnie zaprojektowana bramka logiczna zwana bramką XOR, która jest wykorzystywana w obwodach cyfrowych do działania moduł sumy . Nazywa się to również tzw Ekskluzywna bramka OR lub bramka Ex-OR . Bramka XOR może przyjmować jednocześnie tylko dwa wejścia i dawać sygnał wyjściowy. Wyjście bramki XOR jest wysokie lub logiczne 1 tylko wtedy, gdy jej dwa wejścia są różne.
Właściwości bramki XOR:
Poniżej przedstawiono dwie główne właściwości bramki XOR:
- Może przyjmować tylko dwa wejścia na raz. Nie ma to jak bramka XOR z trzema lub więcej wejściami.
- Wyjście bramki XOR ma stan logiczny 1 lub wysoki, gdy jej wejścia są różne.
Działanie bramki XOR można opisać za pomocą równania matematycznego zwanego wyrażeniem boolowskim. Poniżej znajduje się wyrażenie logiczne określające wynik bramki XOR.
Z=A oplus B
Tutaj Z jest zmienną wyjściową, a A i B są zmiennymi wejściowymi.
Wyrażenie to można również zapisać w następujący sposób:
Z=A overline{B}+overline{A}B
Tabela prawdy bramy XOR:
Tabela prawdy to tabela wejść i wyjść opisująca związek między nimi a działaniem bramki XOR dla różnych kombinacji wejść. Tabela prawdy bramki XOR jest podana poniżej:
Wejście | Wyjście | |
|---|---|---|
A | B | XOR B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Symbol bramki XOR:
Symbol logiczny bramki XOR pokazano na poniższym rysunku.

Symbol bramki XOR
Brama XNOR
Bramka XNOR to kolejny typ bramki logicznej specjalnego przeznaczenia stosowanej do implementacji wyłączna praca w obwodach cyfrowych . Służy do realizacji operacji Exclusive NOR w obwodach cyfrowych. Nazywa się ją także bramką Ex-NOR lub Exclusive NOR. Jest to połączenie dwóch bramek logicznych, mianowicie bramki XOR i bramki NOT. Można to więc wyrazić następująco:
łączenie się z bazą danych w Javie
Brama XNOR = bramka XOR + bramka NOT
Wyjście bramki XNOR ma stan wysoki lub logiczny 1, gdy oba jej wejścia są podobne. W przeciwnym razie wyjście ma stan niski lub logiczne 0. Dlatego bramka XNOR jest używana jako obwód detektora podobieństwa.
Właściwości bramki XNOR:
Poniżej przedstawiono dwie kluczowe właściwości bramki XNOR:
- Bramka XNOR przyjmuje tylko dwa wejścia i generuje jedno wyjście.
- Wyjście bramki XNOR ma stan wysoki lub logiczny 1 tylko wtedy, gdy ma podobne wejścia.
Działanie bramki XNOR można opisać za pomocą równania matematycznego zwanego wyrażeniem boolowskim bramki XNOR. Oto wyrażenie logiczne bramki XNOR.
Y=A odot B
Wyrażenie to możemy również zapisać w następujący sposób:
Y=AB + overline{A} overline{B}
Tutaj A i B są wejściami, a Y jest wyjściem.
Tabela Prawdy Bramy XNOR:
Tabela prawdy bramki XNOR jest podana poniżej. Ta tabela prawdy opisuje relację pomiędzy wejściami i wyjściami bramki XNOR.
Wejście | Wyjście | |
|---|---|---|
A | B | XNOR B |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Symbol Bramy XNOR:
Symbol logiczny bramki XNOR pokazano na poniższym rysunku. Tutaj A i B są wejściami, a Y jest wyjściem.

Symbol bramy XNOR
Zastosowania bramek logicznych
Bramki logiczne są podstawowymi elementami składowymi wszystkich obwodów cyfrowych i urządzeń, takich jak komputery. Oto kilka kluczowych urządzeń cyfrowych, w których do projektowania obwodów wykorzystywane są bramki logiczne:
- Komputery
- Mikroprocesory
- Mikrokontrolery
- Zegarki cyfrowe i inteligentne
- Smartfony itp.
Na podstawie bramek logicznych – często zadawane pytania
Co to są bramki logiczne?
Bramki logiczne to obwody cyfrowe, które wykonują operacje logiczne na dostarczonym im wejściu i wytwarzają odpowiedni sygnał wyjściowy.
Czym są bramy uniwersalne?
Aby zrealizować określony proces logiczny, tworzone są bramki uniwersalne poprzez połączenie dwóch lub więcej bramek podstawowych. Bramkami uniwersalnymi są bramki NAND i NOR.
Jaki jest sygnał wyjściowy bramki NOT po zastosowaniu wejścia 0?
Ponieważ bramka NOT jest falownikiem. W rezultacie, jeśli jako wejście zostanie użyte 0, na wyjściu będzie wartość 1.
Która bramka logiczna nazywana jest falownikiem?
Falownik nazywany jest także bramką NOT. Otrzymany wynik jest odwrotnością sygnału wejściowego.
Jakie jest wyrażenie logiczne dla bramki OR?
Jeśli wejściami są A i B, wówczas wyjście bramki OR można podać jako Y=A+B.
Jakie jest wyrażenie logiczne dla bramki XNOR?
Jeśli wejściami są A i B, wówczas wyjście bramki XNOR można podać jako Y=A.B+A’B’.
