Najpierw zrozumiemy drzewo binarne I drzewo wyszukiwania binarnego oddzielnie, a następnie przyjrzymy się różnicom między drzewem binarnym a drzewem wyszukiwania binarnego.

Co to jest drzewo binarne?

A Drzewo binarne jestWskaźnik do lewego dziecka:Przechowuje odniesienie do lewego węzła podrzędnego.Wskaźnik do odpowiedniego dziecka:Przechowuje odniesienie do prawego węzła podrzędnego.Element danych:Element danych to wartość danych przechowywanych przez węzeł.

Drzewo binarne można przedstawić jako:

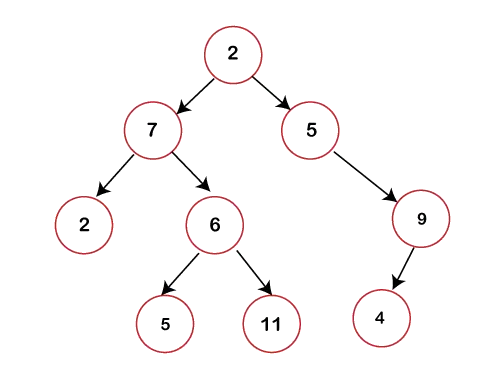
Na powyższym rysunku możemy zauważyć, że każdy węzeł zawiera maksymalnie 2 dzieci. Jeśli jakikolwiek węzeł nie zawiera lewego ani prawego dziecka, wartość wskaźnika w odniesieniu do tego dziecka będzie wynosić NULL.

Podstawowe terminologie stosowane w drzewie binarnym to:

Węzeł główny:Węzeł główny jest pierwszym lub najwyższym węzłem w drzewie binarnym.Węzeł nadrzędny:Kiedy węzeł jest połączony z innym węzłem krawędziami, wówczas węzeł ten nazywany jest węzłem nadrzędnym. W drzewie binarnym węzeł nadrzędny może mieć maksymalnie 2 dzieci.Węzeł podrzędny:Jeśli węzeł ma swojego poprzednika, wówczas węzeł ten nazywany jest a węzeł podrzędny .Węzeł liścia:Węzeł, który nie zawiera żadnego dziecka, nazywany jest a węzeł liścia .Węzeł wewnętrzny:Węzeł, który ma co najmniej 2 dzieci, jest nazywany an węzeł wewnętrzny .Głębokość węzła:Odległość od węzła głównego do danego węzła nazywa się a głębokość węzła . Zapewniamy etykiety wszystkim węzłom, np. węzeł główny jest oznaczony jako 0, ponieważ nie ma głębokości, dzieci węzłów głównych są oznaczone jako 1, dzieci głównego dziecka są oznaczone jako 2.Wysokość:Najdłuższa odległość od węzła głównego do węzła liścia wynosi wysokość węzła .

W drzewie binarnym istnieje jedno drzewo zwane a idealne drzewo binarne . To jest drzewo, w którym wszystkie węzły wewnętrzne muszą zawierać dwa węzły, a wszystkie węzły liściowe muszą znajdować się na tej samej głębokości. W przypadku doskonałego drzewa binarnego całkowitą liczbę węzłów w drzewie binarnym można obliczyć za pomocą następującego równania:

n = 2^m+1-1

który stworzył szkołę

gdzie n to liczba węzłów, m to głębokość węzła.

Co to jest drzewo wyszukiwania binarnego?

A Drzewo wyszukiwania binarnego jest drzewem, które przestrzega określonego porządku rozmieszczenia elementów, podczas gdy drzewo binarne nie ma żadnego porządku. W drzewie wyszukiwania binarnego wartość lewego węzła musi być mniejsza niż węzeł nadrzędny, a wartość prawego węzła musi być większa niż węzeł nadrzędny.

Rozumiemy koncepcję drzewa wyszukiwania binarnego na przykładach.

Na powyższym rysunku możemy zaobserwować, że wartość węzła głównego wynosi 15, czyli jest większa niż wartość wszystkich węzłów w lewym poddrzewie. Wartość węzła głównego jest mniejsza niż wartości wszystkich węzłów w prawym poddrzewie. Teraz przechodzimy do lewego dziecka węzła głównego. 10 jest większe niż 8 i mniejsze niż 12; spełnia również właściwość drzewa wyszukiwania binarnego. Teraz przechodzimy do prawego dziecka węzła głównego; wartość 20 jest większa niż 17 i mniejsza niż 25; spełnia również właściwość drzewa wyszukiwania binarnego. Można zatem powiedzieć, że pokazane powyżej drzewo jest drzewem poszukiwań binarnych.

Teraz, jeśli zmienimy wartość z 12 na 16 w powyższym drzewie binarnym, musimy sprawdzić, czy jest to nadal drzewo wyszukiwania binarnego, czy nie.

sterta i sortowanie po stercie

Wartość węzła głównego wynosi 15, czyli jest większa niż 10, ale mniejsza niż 16, więc nie spełnia właściwości drzewa wyszukiwania binarnego. Dlatego nie jest to drzewo wyszukiwania binarnego.

Operacje na drzewie wyszukiwania binarnego

Na drzewie wyszukiwania binarnego możemy wykonywać operacje wstawiania, usuwania i wyszukiwania. Rozumiemy, jak przeprowadzane jest wyszukiwanie w wyszukiwaniu binarnym. Poniżej pokazano drzewo binarne, na którym musimy wykonać operację wyszukiwania:

Załóżmy, że musimy przeszukać 10 w powyższym drzewie binarnym. Aby przeprowadzić wyszukiwanie binarne, rozważymy wszystkie liczby całkowite w posortowanej tablicy. Najpierw tworzymy pełną listę w przestrzeni wyszukiwania, a wszystkie liczby będą istnieć w przestrzeni wyszukiwania. Przestrzeń poszukiwań jest oznaczona dwoma wskaźnikami, tj. początkiem i końcem. Tablicę powyższego drzewa binarnego można przedstawić jako

Najpierw obliczymy element środkowy i porównamy element środkowy z elementem, który ma być przeszukiwany. Środkowy element jest obliczany przy użyciu n/2. Wartość n wynosi 7; dlatego środkowy element to 15. Środkowy element nie jest równy szukanemu elementowi, tj. 10.

Uwaga: Jeżeli przeszukiwany element jest mniejszy niż element środkowy, to wyszukiwanie zostanie przeprowadzone w lewej połowie; w przeciwnym razie wyszukiwanie zostanie przeprowadzone w prawej połowie. W przypadku równości element zostaje znaleziony.

Ponieważ element do przeszukania jest mniejszy niż element środkowy, wyszukiwanie zostanie przeprowadzone w lewej tablicy. Teraz wyszukiwanie zostało zredukowane do połowy, jak pokazano poniżej:

Środkowy element lewej tablicy to 10, co jest równe szukanemu elementowi.

Ciąg w formacie Java

Złożoność czasowa

W wyszukiwaniu binarnym jest n elementów. Jeśli środkowy element nie jest równy szukanemu elementowi, wówczas przestrzeń poszukiwań zmniejsza się do n/2 i będziemy zmniejszać przestrzeń poszukiwań o n/2, aż znajdziemy element. W całej redukcji, jeśli przejdziemy od n do n/2 do n/4 i tak dalej, to zajmie to log₂n kroków.

Różnice między drzewem binarnym a drzewem wyszukiwania binarnego