Przykład 1:
Zaprojektuj NFA dla tabeli przejściowej, jak podano poniżej:
| Stan obecny | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| pytanie 1 | q3 | mi |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Rozwiązanie:
Diagram przejścia można narysować za pomocą funkcji mapującej podanej w tabeli.
jak przekonwertować ciąg na int w Javie
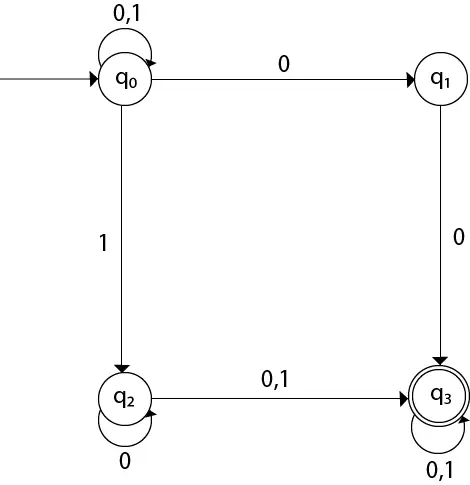
Tutaj,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Przykład 2:
Zaprojektuj NFA z ∑ = {0, 1}, akceptuje wszystkie ciągi kończące się na 01.
Rozwiązanie:

Zatem NFA będzie wyglądać następująco:

Przykład 3:
Zaprojektuj NFA z ∑ = {0, 1}, w którym po podwójnym „1” następuje podwójne „0”.
Rozwiązanie:
FA z podwójną 1 jest następująca:

Bezpośrednio po nim powinno nastąpić podwójne 0.
Następnie,

Teraz przed podwójną liczbą 1 może znajdować się dowolny ciąg znaków 0 i 1. Podobnie po podwójnym liczbie 0 może znajdować się dowolny ciąg znaków składający się z 0 i 1.
Zatem NFA staje się:

Teraz rozważ ciąg 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Przykład 4:
Zaprojektuj NFA, w którym cały ciąg zawiera podciąg 1110.
Rozwiązanie:
Język składa się z całego ciągu zawierającego podciąg 1010. Częściowy diagram przejścia może wyglądać następująco:

Teraz, gdy 1010 może być podciągiem. Dlatego dodamy wejścia 0 i 1, aby można było zachować podciąg 1010 języka. Zatem NFA staje się:

Tabela przejść dla powyższego diagramu przejść może być podana poniżej:
| Stan obecny | 0 | 1 |
|---|---|---|
| →q1 | pytanie 1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | pytanie 5 | *q5 | pytanie 5 | pytanie 5 |
Rozważ ciąg 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Utknąć! Ponieważ nie ma ścieżki z q2 dla symbolu wejściowego 0. Łańcuch 111010 możemy przetworzyć w inny sposób.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Ponieważ stan q5 jest stanem akceptacji. Dostajemy całość zeskanowaną i dotarliśmy do stanu końcowego.
Przykład 5:
Zaprojektuj NFA z ∑ = {0, 1} akceptuje wszystkie ciągi znaków, w których trzeci symbol od prawej strony to zawsze 0.
Rozwiązanie:

W ten sposób trzeci symbol od prawej strony otrzymujemy zawsze jako „0”. NFA może być:

Powyższy obraz to NFA, ponieważ w stanie q0 z wejściem 0 możemy przejść do stanu q0 lub q1.
