Drzewo wyrażeń to drzewo używane do reprezentowania różnych wyrażeń. Do reprezentowania instrukcji wyrażeniowych używana jest drzewiasta struktura danych. W tym drzewie węzeł wewnętrzny zawsze oznacza operatory.
- Węzły liści zawsze oznaczają operandy.
- Operacje są zawsze wykonywane na tych operandach.
- Operator obecny w głębi drzewa ma zawsze najwyższy priorytet.
- Operator, który nie znajduje się zbyt głęboko na drzewie, ma zawsze najniższy priorytet w porównaniu z operatorami leżącymi na głębokości.
- Operand zawsze będzie obecny na głębokości drzewa; dlatego uważa się, że najwyższy priorytet wśród wszystkich operatorów.
- Krótko mówiąc, możemy to podsumować, ponieważ wartość znajdująca się na głębokości drzewa ma najwyższy priorytet w porównaniu z innymi operatorami znajdującymi się na szczycie drzewa.
- Głównym zastosowaniem tych drzew wyrażeń jest to, do czego są przyzwyczajeni oceniać, analizować I modyfikować różne wyrażenia.
- Służy również do sprawdzania łączności każdego operatora w wyrażeniu.
- Na przykład operator + oznacza łączenie lewe, a / to łączenie prawe.
- Dylemat tej asocjatywności został wyjaśniony za pomocą drzew wyrażeń.
- Te drzewa wyrażeń są tworzone przy użyciu gramatyki bezkontekstowej.
- Przed każdą produkcją gramatyczną powiązaliśmy regułę gramatyki bezkontekstowej.
- Reguły te są również znane jako reguły semantyczne i korzystając z nich, możemy łatwo skonstruować drzewa wyrażeń.
- Jest to jedna z głównych części projektu kompilatora i należy do fazy analizy semantycznej.
- W tej analizie semantycznej użyjemy tłumaczeń sterowanych składnią i w formie wyników utworzymy drzewo analizy z adnotacjami.
- Drzewo analizy z adnotacjami to nic innego jak prosta analiza powiązana z atrybutem typu i każdą regułą produkcyjną.
- Głównym celem stosowania drzew wyrażeń jest tworzenie złożonych wyrażeń, które można łatwo ocenić za pomocą tych drzew wyrażeń.
- Jest niezmienna i kiedy utworzymy drzewo wyrażeń, nie możemy go zmienić ani dalej modyfikować.
- Aby dokonać dalszych modyfikacji, konieczne jest zbudowanie w całości nowego drzewa wyrażeń.
- Służy również do rozwiązywania wyrażeń postfiksowych, przedrostkowych i wrostkowych.
Drzewa wyrażeń odgrywają bardzo ważną rolę w reprezentowaniu poziom języka kodu w postaci danych, które przechowywane są głównie w strukturze drzewiastej. Jest również używany w reprezentacji pamięci lambda wyrażenie. Używając drzewiastej struktury danych, możemy wyrazić wyrażenie lambda w bardziej przejrzysty i wyraźny sposób. Najpierw jest tworzony w celu konwersji segmentu kodu na segment danych, aby można było łatwo ocenić wyrażenie.
Drzewo wyrażeń jest drzewem binarnym, w którym każdy węzeł zewnętrzny lub liść odpowiada operandowi, a każdy węzeł wewnętrzny lub nadrzędny odpowiada operatorom, więc na przykład drzewo wyrażeń dla 7 + ((1+8)*3) wyglądałoby następująco:
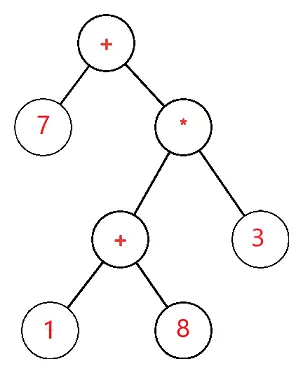
Niech S będzie drzewem wyrażeń
Jeśli S nie jest zerowe, to
Jeśli S.value jest operandem, to
Zwróć wartość S
x = rozwiązanie (S.lewo)
y = rozwiązanie (S.po prawej)
Zwróć oblicz (x, y, wartość S)
W powyższym przykładzie drzewo wyrażeń wykorzystało gramatykę bezkontekstową.
Mamy kilka produkcji związanych z pewnymi regułami produkcji w tej gramatyce, znanych głównie jako zasady semantyczne . Możemy zdefiniować wytwarzanie wyników na podstawie odpowiednich reguł produkcji, korzystając z tych reguł semantycznych. Tutaj użyliśmy parametru value, który obliczy wynik i zwróci go do symbolu początku gramatyki. S.left obliczy lewe dziecko węzła i podobnie prawe dziecko węzła można obliczyć za pomocą parametru S.right.
Użycie drzewa wyrażeń
- Głównym celem stosowania drzew wyrażeń jest tworzenie złożonych wyrażeń, które można łatwo ocenić za pomocą tych drzew wyrażeń.
- Służy również do sprawdzania łączności każdego operatora w wyrażeniu.
- Służy również do rozwiązywania wyrażeń postfiksowych, przedrostkowych i wrostkowych.
Implementacja drzewa wyrażeń
Aby zaimplementować drzewo wyrażeń i napisać jego program, będziemy musieli skorzystać ze struktury danych stosu.
Ponieważ wiemy, że stos opiera się na zasadzie LIFO „ostatnie weszło, pierwsze wyszło”, element danych wepchnięty niedawno do stosu był wyskakiwany, gdy było to wymagane. Do jego implementacji wykorzystywane są dwie główne operacje stosu, push i pop. Za pomocą operacji push wepchniemy element danych na stos, a za pomocą operacji pop usuniemy element danych ze stosu.
Główne funkcje stosu w implementacji drzewa wyrażeń:
W pierwszej kolejności przeskanujemy podane wyrażenie od lewej do prawej, następnie po kolei sprawdzimy zidentyfikowany znak,
- Jeśli zeskanowany znak jest operandem, zastosujemy operację push i wepchniemy go na stos.
- Jeśli zeskanowany znak jest operatorem, zastosujemy do niego operację pop, aby usunąć dwie wartości ze stosu i uczynić je jego dziećmi, a następnie odepchniemy bieżący węzeł nadrzędny na stos.
Implementacja drzewa wyrażeń w języku programowania C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Dane wyjściowe powyższego programu to:
X + Y * Z / W
Implementacja drzewa wyrażeń w języku programowania C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Dane wyjściowe powyższego programu to:
X + Y * Z / W
Implementacja drzewa wyrażeń w języku programowania Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 