logo

TechCodeview

Odwróć drzewo binarne

Biorąc pod uwagę A drzewo binarne zadaniem jest trzepnięcie drzewo binarne w kierunku właściwy kierunek to znaczy zgodnie ze wskazówkami zegara.

Wejście:



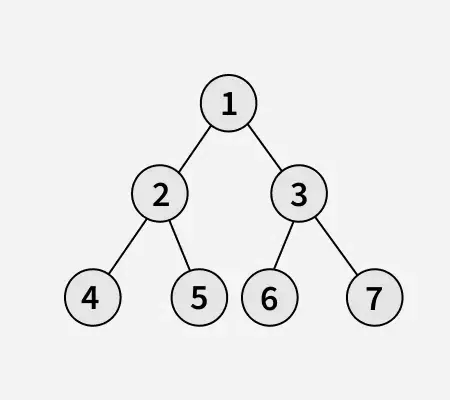
flip-binary-tree-1' title=

Wyjście:

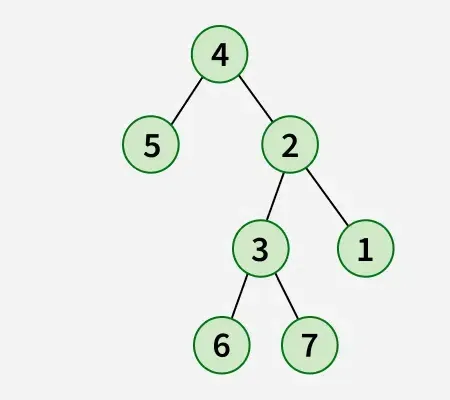
flip-binary-tree-2' loading='lazy' title=


Wyjaśnienie: W operacji odwracania węzeł położony skrajnie na lewo staje się korzeniem odwróconego drzewa, jego rodzic staje się jego prawym dzieckiem, a prawe rodzeństwo staje się jego lewym dzieckiem. To samo należy zrobić rekurencyjnie dla wszystkich węzłów znajdujących się najbardziej na lewo. 



Spis treści

[Oczekiwane podejście - 1] Korzystanie z rekurencji - O(n) czasu i O(n) przestrzeni

Pomysł jest taki rekurencyjnie odwróć drzewo binarne, zamieniając lewy I Prawidłowy poddrzewa każdego węzła. Po odwróceniu struktura drzewa zostanie odwrócona i nowy korzeń drzewa przewrócone drzewo będzie pierwotnym węzłem liścia położonym skrajnie po lewej stronie.

Poniżej znajduje się główne kod rotacji poddrzewa: 



  • root->lewy->lewy = korzeń->prawy
  • root->lewy->prawy = korzeń
  • root->lewy = NULL
  • root->right = NULL
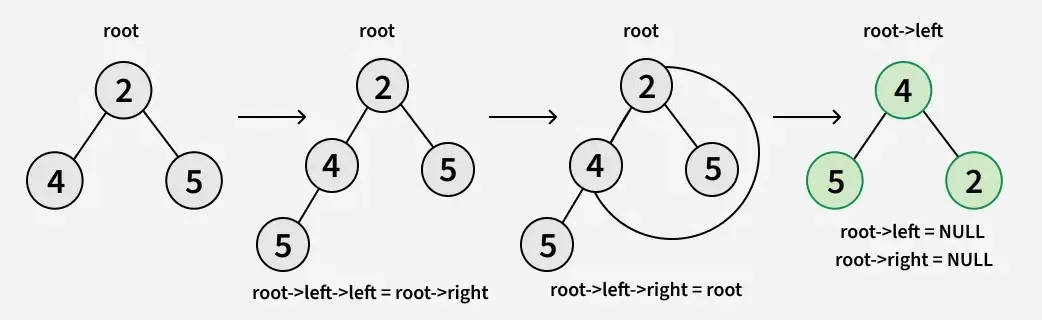
flip-binary-tree-3' loading='lazy' title=

Poniżej implementacja powyższego podejścia: 

C++ 
// C++ program to flip a binary tree  // using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;  Node(int x) {  data = x;   left = right = nullptr;  } }; // method to flip the binary tree iteratively Node* flipBinaryTree(Node* root) {    // Base cases  if (root == nullptr)  return root;  if (root->left == nullptr && root->right == nullptr)  return root;  // Recursively call the same method  Node* flippedRoot = flipBinaryTree(root->left);  // Rearranging main root Node after returning  // from recursive call  root->left->left = root->right;  root->left->right = root;  root->left = root->right = nullptr;  return flippedRoot; } // Iterative method to do level order traversal // line by line void printLevelOrder(Node *root) {    // Base Case  if (root == nullptr) return;  // Create an empty queue for   // level order traversal  queue<Node *> q;  // Enqueue Root and initialize height  q.push(root);  while (1) {    // nodeCount (queue size) indicates number  // of nodes at current level.  int nodeCount = q.size();  if (nodeCount == 0)  break;  // Dequeue all nodes of current level and  // Enqueue all nodes of next level  while (nodeCount > 0) {  Node *node = q.front();  cout << node->data << ' ';  q.pop();  if (node->left != nullptr)  q.push(node->left);  if (node->right != nullptr)  q.push(node->right);  nodeCount--;  }  cout << endl;  } } int main() {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node* root = new Node(1);  root->left = new Node(2);  root->right = new Node(3);  root->right->left = new Node(4);  root->right->right = new Node(5);  root = flipBinaryTree(root);  printLevelOrder(root);  return 0; }
Java 
// Java program to flip a binary tree // using recursion class Node {  int data;  Node left right;  Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Method to flip the binary tree  static Node flipBinaryTree(Node root) {    // Base cases  if (root == null)  return root;  if (root.left == null && root.right == null)  return root;  // Recursively call the same method  Node flippedRoot = flipBinaryTree(root.left);  // Rearranging main root Node after returning  // from recursive call  root.left.left = root.right;  root.left.right = root;  root.left = root.right = null;  return flippedRoot;  }  // Iterative method to do level order   // traversal line by line  static void printLevelOrder(Node root) {    // Base Case  if (root == null) return;  // Create an empty queue for level   // order traversal  java.util.Queue<Node> q = new java.util.LinkedList<>();  // Enqueue Root and initialize height  q.add(root);  while (!q.isEmpty()) {    // nodeCount (queue size) indicates   // number of nodes at current level  int nodeCount = q.size();  // Dequeue all nodes of current level   // and Enqueue all nodes of next level  while (nodeCount > 0) {  Node node = q.poll();  System.out.print(node.data + ' ');  if (node.left != null)  q.add(node.left);  if (node.right != null)  q.add(node.right);  nodeCount--;  }  System.out.println();  }  }  public static void main(String[] args) {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.right.left = new Node(4);  root.right.right = new Node(5);  root = flipBinaryTree(root);  printLevelOrder(root);  } }
Python 
# Python program to flip a binary # tree using recursion class Node: def __init__(self x): self.data = x self.left = None self.right = None def flipBinaryTree(root): # Base cases if root is None: return root if root.left is None and root.right is None: return root # Recursively call the same method flippedRoot = flipBinaryTree(root.left) # Rearranging main root Node after returning # from recursive call root.left.left = root.right root.left.right = root root.left = root.right = None return flippedRoot # Iterative method to do level order  # traversal line by line def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue for  # level order traversal queue = [] queue.append(root) while queue: nodeCount = len(queue) while nodeCount > 0: node = queue.pop(0) print(node.data end=' ') if node.left is not None: queue.append(node.left) if node.right is not None: queue.append(node.right) nodeCount -= 1 print() if __name__ == '__main__': # Make a binary tree # # 1 # /  # 2 3 # /  # 4 5  root = Node(1) root.left = Node(2) root.right = Node(3) root.right.left = Node(4) root.right.right = Node(5) root = flipBinaryTree(root) printLevelOrder(root)
C# 
// C# program to flip a binary tree  // using recursion using System; using System.Collections.Generic; class Node {  public int data;  public Node left right;  public Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Method to flip the binary tree  static Node FlipBinaryTree(Node root) {  if (root == null)  return root;  if (root.left == null && root.right == null)  return root;  // Recursively call the same method  Node flippedRoot = FlipBinaryTree(root.left);  // Rearranging main root Node after returning  // from recursive call  root.left.left = root.right;  root.left.right = root;  root.left = root.right = null;  return flippedRoot;  }  // Iterative method to do level order   // traversal line by line  static void PrintLevelOrder(Node root) {  if (root == null) return;  // Create an empty queue for level   // order traversal  Queue<Node> q = new Queue<Node>();  // Enqueue Root and initialize height  q.Enqueue(root);  while (q.Count > 0) {    // nodeCount (queue size) indicates   // number of nodes at current level  int nodeCount = q.Count;  // Dequeue all nodes of current level   // and Enqueue all nodes of next level  while (nodeCount > 0) {  Node node = q.Dequeue();  Console.Write(node.data + ' ');  if (node.left != null)  q.Enqueue(node.left);  if (node.right != null)  q.Enqueue(node.right);  nodeCount--;  }  Console.WriteLine();  }  }  static void Main(string[] args) {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.right.left = new Node(4);  root.right.right = new Node(5);    root = FlipBinaryTree(root);  PrintLevelOrder(root);  } }
JavaScript 
// JavaScript program to flip a binary  // tree using recursion class Node {  constructor(x) {  this.data = x;  this.left = null;  this.right = null;  } } // Method to flip the binary tree function flipBinaryTree(root) {    if (root === null) return root;  if (root.left === null && root.right === null) return root;  // Recursively call the same method  const flippedRoot = flipBinaryTree(root.left);  // Rearranging main root Node after returning  // from recursive call  root.left.left = root.right;  root.left.right = root;  root.left = root.right = null;  return flippedRoot; } // Iterative method to do level order traversal // line by line function printLevelOrder(root) {  if (root === null) return;  // Create an empty queue for level  // order traversal  const queue = [root];  while (queue.length > 0) {  let nodeCount = queue.length;  while (nodeCount > 0) {  const node = queue.shift();  console.log(node.data + ' ');  if (node.left !== null) queue.push(node.left);  if (node.right !== null) queue.push(node.right);  nodeCount--;  }  console.log();  } } // Make a binary tree // // 1 // /  // 2 3 // /  // 4 5  const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.right.left = new Node(4); root.right.right = new Node(5); const flippedRoot = flipBinaryTree(root); printLevelOrder(flippedRoot);

Wyjście 
2 3 1 4 5

[Oczekiwane podejście – 2] Podejście iteracyjne - O(n) czasu i O(n) przestrzeni

The rozwiązanie iteracyjne stosuje to samo podejście, co rekurencyjne jedyną rzeczą, na którą musimy zwrócić uwagę, jest oszczędność informacje o węźle, które będą nadpisany . 

Poniżej implementacja powyższego podejścia: 

C++ 
// C++ program to flip a binary tree using // iterative approach #include    using namespace std; class Node { public:  int data;  Node *left *right;  Node(int x) {  data = x;   left = right = nullptr;  } }; // Method to flip the binary tree iteratively Node* flipBinaryTree(Node* root) {    // intiliazing the pointers to do the   // swapping and storing states  Node *curr = root *next = nullptr   *prev = nullptr *ptr = nullptr;  while (curr != nullptr) {    // pointing the next pointer to the  // current next of left  next = curr->left;    // making the right child of prev   // as curr left child  curr->left = ptr;  // storign the right child of  // curr in temp  ptr = curr->right;  curr->right = prev;  prev = curr;  curr = next;  }  return prev; } // Iterative method to do level order traversal // line by line void printLevelOrder(Node *root) {    // Base Case  if (root == nullptr) return;  // Create an empty queue for level   // order traversal  queue<Node *> q;  // Enqueue Root and   // initialize height  q.push(root);  while (1) {    // nodeCount (queue size) indicates number  // of nodes at current level.  int nodeCount = q.size();  if (nodeCount == 0)  break;  // Dequeue all nodes of current level and  // Enqueue all nodes of next level  while (nodeCount > 0) {    Node *node = q.front();  cout << node->data << ' ';  q.pop();  if (node->left != nullptr)  q.push(node->left);  if (node->right != nullptr)  q.push(node->right);  nodeCount--;  }  cout << endl;  } } int main() {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node* root = new Node(1);  root->left = new Node(2);  root->right = new Node(3);  root->right->left = new Node(4);  root->right->right = new Node(5);  root = flipBinaryTree(root);  printLevelOrder(root);  return 0; }
Java 
// Java program to flip a binary tree // using iterative approach class Node {  int data;  Node left right;  Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Method to flip the binary tree  static Node flipBinaryTree(Node root) {    // Initializing the pointers to do the   // swapping and storing states  Node curr = root;  Node next = null;  Node prev = null;  Node ptr = null;  while (curr != null) {    // Pointing the next pointer to  // the current next of left  next = curr.left;  // Making the right child of   // prev as curr left child  curr.left = ptr;  // Storing the right child   // of curr in ptr  ptr = curr.right;  curr.right = prev;  prev = curr;  curr = next;  }  return prev;  }  // Iterative method to do level order  // traversal line by line  static void printLevelOrder(Node root) {    if (root == null) return;  // Create an empty queue for level   // order traversal  java.util.Queue<Node> q = new java.util.LinkedList<>();  // Enqueue Root and initialize   // height  q.add(root);  while (!q.isEmpty()) {    // nodeCount (queue size) indicates   // number of nodes at current level  int nodeCount = q.size();  // Dequeue all nodes of current level   // and Enqueue all nodes of next level  while (nodeCount > 0) {  Node node = q.poll();  System.out.print(node.data + ' ');  if (node.left != null)  q.add(node.left);  if (node.right != null)  q.add(node.right);  nodeCount--;  }  System.out.println();  }  }  public static void main(String[] args) {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.right.left = new Node(4);  root.right.right = new Node(5);  root = flipBinaryTree(root);  printLevelOrder(root);  } }
Python 
# Python program to flip a binary tree # using iterative approach class Node: def __init__(self x): self.data = x self.left = None self.right = None # Method to flip the binary tree # iteratively def flip_binary_tree(root): # Initializing the pointers to do # the swapping and storing states curr = root next = None prev = None ptr = None while curr is not None: # Pointing the next pointer to the # current next of left next = curr.left # Making the right child of prev # as curr left child curr.left = ptr # Storing the right child of # curr in ptr ptr = curr.right curr.right = prev prev = curr curr = next return prev # Iterative method to do level order # traversal line by line def printLevelOrder(root): if root is None: return # Create an empty queue for # level order traversal queue = [] queue.append(root) while queue: nodeCount = len(queue) while nodeCount > 0: node = queue.pop(0) print(node.data end=' ') if node.left is not None: queue.append(node.left) if node.right is not None: queue.append(node.right) nodeCount -= 1 print() if __name__ == '__main__': # Make a binary tree # # 1 # /  # 2 3 # /  # 4 5 root = Node(1) root.left = Node(2) root.right = Node(3) root.right.left = Node(4) root.right.right = Node(5) root = flip_binary_tree(root) printLevelOrder(root)
C# 
// C# program to flip a binary tree // using iterative approach using System; using System.Collections.Generic; class Node {  public int data;  public Node left right;  public Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Method to flip the binary tree  static Node FlipBinaryTree(Node root) {    // Initializing the pointers to   // do the swapping and storing states  Node curr = root;  Node next = null;  Node prev = null;  Node ptr = null;  while (curr != null) {    // Pointing the next pointer to   // the current next of left  next = curr.left;  // Making the right child of prev  // as curr left child  curr.left = ptr;  // Storing the right child  // of curr in ptr  ptr = curr.right;  curr.right = prev;  prev = curr;  curr = next;  }  return prev;  }  // Iterative method to do level order  // traversal line by line  static void PrintLevelOrder(Node root) {  if (root == null) return;  // Create an empty queue for  // level order traversal  Queue<Node> q = new Queue<Node>();  // Enqueue Root and initialize height  q.Enqueue(root);  while (q.Count > 0) {    // nodeCount (queue size) indicates   // number of nodes at current level  int nodeCount = q.Count;  // Dequeue all nodes of current level   // and Enqueue all nodes of next level  while (nodeCount > 0) {  Node node = q.Dequeue();  Console.Write(node.data + ' ');  if (node.left != null)  q.Enqueue(node.left);  if (node.right != null)  q.Enqueue(node.right);  nodeCount--;  }  Console.WriteLine();  }  }  static void Main(string[] args) {    // Make a binary tree  //  // 1  // /   // 2 3  // /   // 4 5   Node root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.right.left = new Node(4);  root.right.right = new Node(5);  root = FlipBinaryTree(root);  PrintLevelOrder(root);  } }
JavaScript 
// JavaScript program to flip a binary  // tree using iterative approach class Node {  constructor(x) {  this.data = x;  this.left = null;  this.right = null;  } } function flipBinaryTree(root) {  // Initializing the pointers to do the  // swapping and storing states  let curr = root;  let next = null;  let prev = null;  let ptr = null;  while (curr !== null) {    // Pointing the next pointer to the   // current next of left  next = curr.left;  // Making the right child of prev  // as curr left child  curr.left = ptr;  // Storing the right child of   // curr in ptr  ptr = curr.right;  curr.right = prev;  prev = curr;  curr = next;  }  return prev; } // Iterative method to do level order // traversal line by line function printLevelOrder(root) {  if (root === null) return;  // Create an empty queue for  // level order traversal  const queue = [root];  while (queue.length > 0) {  let nodeCount = queue.length;  while (nodeCount > 0) {  const node = queue.shift();  console.log(node.data + ' ');  if (node.left !== null) queue.push(node.left);  if (node.right !== null) queue.push(node.right);  nodeCount--;  }  console.log();  } } // Make a binary tree // // 1 // /  // 2 3 // /  // 4 5  const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.right.left = new Node(4); root.right.right = new Node(5); const flippedRoot = flipBinaryTree(root); printLevelOrder(flippedRoot);

Wyjście 
2 3 1 4 5