Algorytm Forda-Fulkersona jest szeroko stosowanym algorytmem do rozwiązywania problemu maksymalnego przepływu w sieci przepływowej. Problem maksymalnego przepływu polega na określeniu maksymalnej wielkości przepływu, która może zostać wysłana z wierzchołka źródłowego do wierzchołka ujścia na ukierunkowanym wykresie ważonym, z zastrzeżeniem ograniczeń przepustowości na krawędziach.
Algorytm działa poprzez iteracyjne znajdowanie ścieżki zwiększającej, czyli ścieżki od źródła do ujścia na wykresie rezydualnym, tj. wykresie uzyskanym poprzez odjęcie przepływu prądu od pojemności każdej krawędzi. Następnie algorytm zwiększa przepływ wzdłuż tej ścieżki o maksymalną możliwą wielkość, czyli minimalną przepustowość krawędzi wzdłuż ścieżki.
Problem:
Biorąc pod uwagę wykres przedstawiający sieć przepływową, w której każda krawędź ma przepustowość. Ponadto, biorąc pod uwagę dwa wierzchołki źródło „s” i zlew „t” na wykresie, znajdź maksymalny możliwy przepływ od s do t przy następujących ograniczeniach:
- Przepływ na krawędzi nie przekracza zadanej przepustowości krawędzi.
- Przepływ przychodzący jest równy przepływowi wychodzącemu dla każdego wierzchołka z wyjątkiem s i t.
Rozważmy na przykład poniższy wykres z książki CLRS.
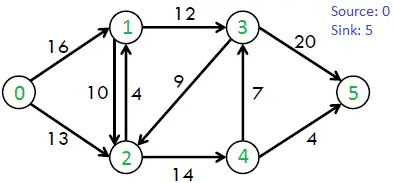
Maksymalny możliwy przepływ na powyższym wykresie wynosi 23.

Warunek wstępny: Wprowadzenie do problemu maksymalnego przepływu
Algorytm Forda-Fulkersona
Poniżej przedstawiono prostą ideę algorytmu Forda-Fulkersona:
- Zacznij od przepływu początkowego wynoszącego 0.
- Chociaż istnieje ścieżka wzmacniająca od źródła do ujścia:
- Znajdź ścieżkę rozszerzającą, korzystając z dowolnego algorytmu wyszukiwania ścieżki, takiego jak przeszukiwanie wszerz lub przeszukiwanie w głąb.
- Określ wielkość przepływu, który może zostać przesłany wzdłuż ścieżki wzmacniającej, czyli minimalną pojemność resztkową wzdłuż krawędzi ścieżki.
- Zwiększyć przepływ wzdłuż ścieżki wzmacniającej o określoną wartość.
- Zwróć maksymalny przepływ.
Złożoność czasowa: Złożoność czasowa powyższego algorytmu wynosi O(max_flow * E). Wykonujemy pętlę, gdy istnieje ścieżka wzmacniająca. W najgorszym przypadku możemy dodać 1 jednostkę przepływu w każdej iteracji. Zatem złożoność czasowa wynosi O(max_flow * E).
witryny takie jak bedpage
Jak zaimplementować powyższy prosty algorytm?
Zdefiniujmy najpierw pojęcie wykresu resztowego, które jest potrzebne do zrozumienia implementacji.
Wykres pozostałości sieci przepływowej jest wykresem przedstawiającym dodatkowy możliwy przepływ. Jeśli na wykresie resztowym istnieje ścieżka od źródła do ujścia, wówczas możliwe jest dodanie przepływu. Każda krawędź grafu resztowego ma wartość zwaną pojemność resztkowa która jest równa pierwotnej pojemności krawędzi pomniejszonej o przepływ prądu. Pojemność resztkowa to w zasadzie pojemność prądowa krawędzi.
Porozmawiajmy teraz o szczegółach implementacji. Pojemność resztowa wynosi 0, jeśli pomiędzy dwoma wierzchołkami grafu resztowego nie ma krawędzi. Możemy zainicjować wykres resztkowy jako wykres oryginalny, ponieważ nie ma przepływu początkowego i początkowo wydajność resztkowa jest równa wydajności pierwotnej. Aby znaleźć ścieżkę rozszerzającą, możemy wykonać BFS lub DFS grafu reszt. W poniższej implementacji użyliśmy BFS. Korzystając z BFS, możemy dowiedzieć się, czy istnieje ścieżka od źródła do ujścia. BFS buduje także tablicę nadrzędną []. Używając tablicy parent[], przechodzimy przez znalezioną ścieżkę i znajdujemy możliwy przepływ przez tę ścieżkę, znajdując minimalną pojemność resztkową na ścieżce. Później dodamy znaleziony przepływ po ścieżce do przepływu całkowitego.
bdrzewo i b drzewo
Ważną rzeczą jest to, że musimy zaktualizować pozostałe zdolności produkcyjne na wykresie resztkowym. Odejmujemy przepływ ścieżki od wszystkich krawędzi wzdłuż ścieżki i dodajemy przepływ ścieżki wzdłuż odwrotnych krawędzi. Musimy dodać przepływ ścieżki wzdłuż odwrotnych krawędzi, ponieważ później może zaistnieć potrzeba skierowania przepływu w odwrotnym kierunku (patrz na przykład poniższy link).
Poniżej znajduje się implementacja algorytmu Forda-Fulkersona. Dla uproszczenia wykres jest reprezentowany jako macierz 2D.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Jeśli znajdziemy połączenie z węzłem ujścia, // to nie ma już sensu w BFS. // Musimy tylko ustawić jego rodzica i możemy zwrócić // true if (v == t) { parent[ v] = ty; zwróć wartość true; } q.push(v); rodzic[v] = ty; odwiedziliśmy[v] = prawda; } } } // Nie osiągnęliśmy ujścia w BFS, zaczynając od źródła, więc // zwróć fałsz return false; } // Zwraca maksymalny przepływ od s do t na danym wykresie int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Utwórz wykres reszt i wypełnij wykres reszt // danymi pojemnościami na oryginalnym wykresie jako // wydajności reszt na wykresie reszt int rGraph[V] [V]; // Wykres reszt, gdzie rGraph[i][j] // wskazuje resztkową pojemność krawędzi // od i do j (jeśli istnieje krawędź. Jeśli // rGraph[i][j] wynosi 0, to jej nie ma) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // Ta tablica jest wypełniana przez BFS i // zapisuje ścieżkę int max_flow = 0; // Początkowo nie ma przepływu // Zwiększ przepływ, gdy istnieje ścieżka od źródła do // ujścia while (bfs(rGraph, s, t, parent)) { // Znajdź minimalną pojemność resztkową krawędzi wzdłuż // ścieżki wypełnionej przez BFS. Lub możemy powiedzieć, // znajdź maksymalny przepływ przez znalezioną ścieżkę int path_flow = INT_MAX; for (v = t; v != s; v = parent[v]) { u = parent[v]; path_flow = min(path_flow, rGraph[u][v]); } // zaktualizuj resztkowe możliwości krawędzi i // odwróć krawędzie wzdłuż ścieżki dla (v = t; v != s; v = rodzic[v]) { u = rodzic[v]; rGraph[u][v] -= ścieżka_przepływu; rGraph[v][u] += ścieżka_przepływu; } // Dodaj przepływ ścieżki do ogólnego przepływu max_flow += ścieżka_przepływu; // Zwraca całkowity przepływ return max_flow; } // Program sterownika testujący powyższe funkcje int main() { // Stwórzmy wykres pokazany w powyższym przykładzie int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Jawa
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Jeśli znajdziemy połączenie z węzłem // ujściem, to nie ma już sensu w BFS // Musimy tylko ustawić jego rodzica // i możemy zwrócić wartość true if (v == t) { rodzic[ v] = ty; zwróć wartość true; } kolejka.add(v); rodzic[v] = ty; odwiedziliśmy[v] = prawda; } } } // Nie osiągnęliśmy ujścia w BFS, zaczynając od źródła, // więc zwróć fałsz return false; } // Zwraca maksymalny przepływ od s do t w danym // graph int fordFulkerson(int graph[][], int s, int t) { int u, v; // Utwórz wykres reszt i wypełnij wykres reszt // wykresami reszt o danych pojemnościach na oryginalnym wykresie // jako pojemności reszt na wykresie reszt // Wykres reszt, gdzie rGraph[i][j] wskazuje // resztkową pojemność krawędzi od i do j (jeśli // istnieje krawędź. Jeśli rGraph[i][j] wynosi 0, to // nie ma) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // Ta tablica jest wypełniana przez BFS i przechowuje ścieżkę int parent[] = new int[ V]; int max_flow = 0; // Początkowo nie ma przepływu // Zwiększ przepływ, gdy istnieje ścieżka od źródła // do ujścia póki (bfs(rGraph, s, t, parent)) { // Znajdź minimalną pojemność resztkową krawędzi // wzdłuż ścieżki wypełnionej przez BFS. Lub możemy powiedzieć // znajdź maksymalny przepływ przez znalezioną ścieżkę int path_flow = Integer.MAX_VALUE; for (v = t; v != s; v = parent[v ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v] } // aktualizuj resztkowe możliwości krawędzi i // odwrotne krawędzie wzdłuż ścieżki dla (v = t; v != s; v = rodzic[v]) { u = rodzic[v]; rGraph[u][v] -= ścieżka_przepływu; rGraph[v][u] += ścieżka_przepływu } // Dodaj przepływ ścieżki do całości; flow max_flow += path_flow; } // Zwraca ogólny przepływ return max_flow; } // Program sterownika testujący powyższe funkcje public static void main(String[] args) rzuca java.lang.Exception { // Stwórzmy pokazany wykres w powyższym przykładzie int graph[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = nowy MaxFlow(); System.out.println('Maksymalny możliwy przepływ to ' + m.fordFulkerson(wykres, 0, 5)); } }> |
>
jsp
>
Pyton
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
Zrzucony rdzeń błędu segmentacji
>
JavaScript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Jeśli znajdziemy połączenie z węzłem // ujściem, to nie ma już sensu w BFS // Musimy tylko ustawić jego rodzica // i możemy zwrócić wartość true if (v == t) { rodzic[ v] = ty; zwróć wartość true; } kolejka.push(v); rodzic[v] = ty; odwiedziliśmy[v] = prawda; } } } // Nie osiągnęliśmy ujścia w BFS, zaczynając // od źródła, więc zwróć fałsz return false; } // Zwraca maksymalny przepływ od s do t w // podanej funkcji wykresu fordFulkerson(graph, s, t) { let u, v; // Utwórz wykres reszt i wypełnij // wykres reszt podanymi pojemnościami // na oryginalnym wykresie jako resztki // pojemności na wykresie reszt // Wykres reszt, gdzie rGraph[i][j] // wskazuje resztkową pojemność krawędzi // / od i do j (jeśli istnieje krawędź. // Jeśli rGraph[i][j] wynosi 0, to // nie ma) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Ta tablica jest wypełniana przez BFS i do przechowywania ścieżki let parent = new Array(V); // Początkowo nie ma przepływu let max_flow = 0; // Zwiększ przepływ, gdy istnieje // jest ścieżka od źródła do ujścia while (bfs(rGraph, s, t , nadrzędny)) { // Znajdź minimalną pojemność resztkową krawędzi // wzdłuż ścieżki wypełnionej przez BFS. Lub możemy powiedzieć // znajdź maksymalny przepływ przez znalezioną ścieżkę niech path_flow = Number.MAX_VALUE; ; v != s; v = rodzic[v]) { u = rodzic[v]; path_flow = Math.min(path_flow, rGraph[u][v] } // Aktualizuj pozostałe możliwości krawędzi i // odwróć krawędzie wzdłuż ścieżki for(v = t; v != s; v = rodzic[v]) { u = rodzic[v]; rGraph[u][v] -= rGraph[v][u] + = path_flow; } // Dodaj przepływ ścieżki do całkowitego przepływu max_flow += path_flow; } // Zwróć całkowity przepływ return max_flow; } // Kod sterownika // Utwórzmy wykres pokazany w powyższym przykładzie let graph = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ]]; document.write('Maksymalny możliwy przepływ to ' + fordFulkerson(wykres, 0, 5)); // Ten kod został napisany przez avanitrachhadiya2155> |
>
znak Java na liczbę całkowitą
>Wyjście
The maximum possible flow is 23>
Złożoność czasowa: O(|V| * E^2) , gdzie E jest liczbą krawędzi, a V jest liczbą wierzchołków.
Złożoność przestrzenna :O(V) , gdy utworzyliśmy kolejkę.
Powyższa implementacja algorytmu Forda Fulkersona nosi nazwę Algorytm Edmondsa-Karpa . Pomysł Edmondsa-Karpa polega na użyciu BFS w implementacji Forda Fulkersona, ponieważ BFS zawsze wybiera ścieżkę z minimalną liczbą krawędzi. Gdy używany jest BFS, złożoność czasową w najgorszym przypadku można zredukować do O (VE2). Powyższa implementacja wykorzystuje jednak macierz sąsiedztwa, gdzie BFS przyjmuje O(V2) czasu, złożoność czasowa powyższej implementacji wynosi O(EV3) (Wspominać Książka CLRS dla dowodu złożoności czasowej)
Jest to istotny problem, gdyż pojawia się w wielu praktycznych sytuacjach. Przykłady obejmują maksymalizację transportu przy danych ograniczeniach ruchu, maksymalizację przepływu pakietów w sieciach komputerowych.
Algorytm Dinc’a dla Max-Flow.
Ćwiczenia:
Zmodyfikuj powyższą implementację tak, aby działała w O(VE2) czas.
