Przed zrozumieniem drzewo B I Drzewo B+ różnice, powinniśmy znać drzewo B i drzewo B+ osobno.
Co to jest drzewo B?
drzewo B jest drzewem samorównoważącym i jest drzewem m-drogowym, gdzie m określa porządek drzewa. Bdrzewo jest uogólnieniem Drzewo wyszukiwania binarnego w którym węzeł może mieć więcej niż jeden klucz i więcej niż dwoje dzieci, w zależności od wartości M . W drzewie B dane są określone w posortowanej kolejności, z niższymi wartościami w lewym poddrzewie i wyższymi wartościami w prawym poddrzewie.
gimp usuń znak wodny
Właściwości drzewa B
Poniżej przedstawiono właściwości drzewa B:
- W drzewie B wszystkie węzły liściowe muszą znajdować się na tym samym poziomie, natomiast w przypadku drzewa binarnego węzły liściowe mogą znajdować się na różnych poziomach.
Rozumiemy tę właściwość na przykładzie.
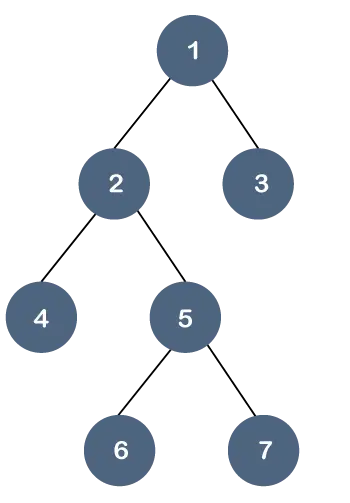
W powyższym drzewie wszystkie węzły liści nie są na tym samym poziomie, ale mają najwięcej dwójki dzieci. Można zatem powiedzieć, że powyższe drzewo jest a drzewo binarne ale nie drzewo B.
- Jeśli Btree ma rząd m, wówczas każdy węzeł może mieć maksymalnie M W przypadku minimalnych dzieci węzły liściowe mają zero dzieci, węzeł główny ma dwójkę dzieci, a węzły wewnętrzne mają pułap m/2.
- Każdy węzeł może mieć maksymalnie (m-1) kluczy. Na przykład, jeśli wartość m wynosi 5, wówczas maksymalna wartość kluczy wynosi 4.
- Węzeł główny ma co najmniej jeden klucz, podczas gdy wszystkie pozostałe węzły z wyjątkiem węzła głównego mają (sufit m/2 minus - 1) minimalną liczbę kluczy.
- Jeśli dokonamy wstawienia w drzewie B, wówczas węzeł jest zawsze wstawiany w węźle liścia.
Załóżmy, że chcemy utworzyć drzewo B rzędu 3, wstawiając wartości od 1 do 10.
Krok 1: Najpierw tworzymy węzeł z 1 wartością, jak pokazano poniżej:

Krok 2: Następnym elementem jest liczba 2, która następuje po liczbie 1, jak pokazano poniżej:

Krok 3: Następny element to 3 i jest wstawiany po 2, jak pokazano poniżej:

Ponieważ wiemy, że każdy węzeł może mieć maksymalnie 2 klucze, dlatego podzielimy ten węzeł przez środkowy element. Środkowy element ma wartość 2, więc przesuwa się do swojego rodzica. Węzeł 2 nie ma żadnego rodzica, więc stanie się węzłem głównym, jak pokazano poniżej:

Krok 4: Następnym elementem jest 4. Ponieważ 4 jest większe niż 2 i 3, zostanie ono dodane po 3, jak pokazano poniżej:

Krok 5: Następnym elementem jest 5. Ponieważ 5 jest większe od 2, 3 i 4, zostanie ono dodane po 4, jak pokazano poniżej:

Ponieważ wiemy, że każdy węzeł może mieć maksymalnie 2 klucze, dlatego podzielimy ten węzeł przez środkowy element. Środkowy element ma wartość 4, więc przesuwa się do swojego rodzica. Rodziciem jest węzeł 2; dlatego 4 zostanie dodane po 2, jak pokazano poniżej:

Krok 6: Następnym elementem jest 6. Ponieważ 6 jest większe niż 2, 4 i 5, więc 6 pojawi się po 5, jak pokazano poniżej:

Krok 7: Następnym elementem jest 7. Ponieważ 7 jest większe niż 2, 4, 5 i 6, więc 7 pojawi się po 6, jak pokazano poniżej:

Ponieważ wiemy, że każdy węzeł może mieć maksymalnie 2 klucze, dlatego podzielimy ten węzeł przez środkowy element. Środkowy element to 6, więc przesuwa się do swojego rodzica, jak pokazano poniżej:

Ale 6 nie można dodać po 4, ponieważ węzeł może mieć maksymalnie 2 klucze, więc podzielimy ten węzeł przez środkowy element. Środkowy element ma wartość 4, więc przesuwa się do swojego rodzica. Ponieważ węzeł 4 nie ma żadnego rodzica, węzeł 4 stanie się węzłem głównym, jak pokazano poniżej:

Co to jest drzewo B+?
The Drzewo B+ jest również znane jako zaawansowane drzewo samobalansujące, ponieważ każda ścieżka od korzenia drzewa do liścia drzewa ma tę samą długość. Tutaj ta sama długość oznacza, że wszystkie węzły liściowe występują na tym samym poziomie. Nie będzie tak, że część węzłów liściowych pojawi się na poziomie trzecim, a część na drugim.
Indeks drzewa B+ jest uważany za indeks wielopoziomowy, ale struktura drzewa B+ nie jest podobna do plików sekwencyjnych indeksu wielopoziomowego.
Dlaczego używa się drzewa B+?
Drzewo B+ służy do bardzo wydajnego przechowywania rekordów poprzez przechowywanie rekordów w sposób indeksowany przy użyciu indeksowanej struktury drzewa B+. Dzięki wielopoziomowemu indeksowaniu dostęp do danych staje się szybszy i łatwiejszy.
Struktura węzła drzewa B+
Struktura węzłów drzewa B+ zawiera wskaźniki i wartości kluczy pokazane na poniższym rysunku:

Jak możemy zaobserwować w powyższej strukturze węzłów drzewa B+, zawiera ona n-1 wartości kluczy (k1do kn-1) i n wskaźników (s1szczytN).
Wartości kluczy wyszukiwania umieszczone w węźle są przechowywane w posortowanej kolejności. Zatem, jeśli I
Ograniczenia dotyczące różnych typów węzłów
Niech „b” będzie porządkiem drzewa B+.
Węzeł inny niż liść
porównanie w Javie
Niech „m” oznacza liczbę dzieci węzła, wówczas relację pomiędzy porządkiem drzewa a liczbą dzieci można przedstawić jako:

Niech k reprezentuje wartości klucza wyszukiwania. Relację pomiędzy kolejnością drzewa a kluczem wyszukiwania można przedstawić jako:
Ponieważ wiemy, że liczba wskaźników jest równa wartościom klucza wyszukiwania plus 1, więc matematycznie można to zapisać jako:
Liczba wskaźników (lub dzieci) = liczba kluczy wyszukiwania + 1
Zatem maksymalna liczba wskaźników będzie wynosić „b”, a minimalna liczba wskaźników będzie funkcją górną b/2.
Węzeł liścia
Węzeł liścia to węzeł występujący na ostatnim poziomie drzewa B+, a każdy węzeł liścia używa tylko jednego wskaźnika do łączenia się ze sobą w celu zapewnienia sekwencyjnego dostępu na poziomie liścia.
W węźle liścia maksymalna liczba dzieci wynosi:

Maksymalna liczba kluczy wyszukiwania wynosi:

Węzeł główny
Maksymalna liczba dzieci w przypadku węzła głównego wynosi: b
Minimalna liczba dzieci to: 2
Przypadki specjalne w drzewie B+
Przypadek 1: Jeśli węzeł główny jest jedynym węzłem w drzewie. W tym przypadku węzeł główny staje się węzłem liścia.
W tym przypadku maksymalna liczba dzieci wynosi 1, czyli sam węzeł główny, natomiast minimalna liczba dzieci wynosi b-1, czyli jest taka sama jak węzeł liścia.
Reprezentacja węzła liścia w drzewie B+

Na powyższym rysunku „.” reprezentuje wskaźnik, podczas gdy 10, 20 i 30 to wartości kluczowe. Wskaźnik zawiera adres, pod którym przechowywana jest wartość klucza, jak pokazano na powyższym rysunku.
Przykład drzewa B+

Na powyższym rysunku węzeł zawiera trzy wartości kluczowe, tj. 9, 16 i 25. Wskaźnik pojawiający się przed 9 zawiera kluczowe wartości mniejsze niż 9 reprezentowane przez kI. Wskaźnik pojawiający się przed liczbą 16 zawiera wartości kluczy większe lub równe 9, ale mniejsze niż 16 reprezentowane przez kj. Wskaźnik pojawiający się przed liczbą 25 zawiera wartości klucza większe lub równe 16, ale mniejsze niż 25 reprezentowane przez kN.
Różnice pomiędzy drzewem B i drzewem B+

Poniżej przedstawiono różnice między drzewem B i drzewem B+:
| drzewo B | Drzewo B+ |
|---|---|
| W drzewie B wszystkie klucze i rekordy są przechowywane zarówno w węzłach wewnętrznych, jak i liściach. | W drzewie B+ klucze są indeksami przechowywanymi w węzłach wewnętrznych, a rekordy są przechowywane w węzłach-liście. |
| W drzewie B nie można przechowywać kluczy wielokrotnie, co oznacza, że nie dochodzi do powielania kluczy i rekordów. | W drzewie B+ może występować redundancja występowania kluczy. W tym przypadku rekordy przechowywane są w węzłach-liście, natomiast klucze są przechowywane w węzłach wewnętrznych, więc w węzłach wewnętrznych mogą znajdować się klucze nadmiarowe. |
| W drzewie Btree węzły liści nie są ze sobą połączone. | W drzewie B+ węzły liści są ze sobą połączone, aby zapewnić dostęp sekwencyjny. |
| W Btree wyszukiwanie nie jest zbyt wydajne, ponieważ rekordy są przechowywane w węzłach liściowych lub wewnętrznych. | W drzewie B+ wyszukiwanie jest bardzo wydajne i szybsze, ponieważ wszystkie rekordy przechowywane są w węzłach-liście. |
| Usuwanie węzłów wewnętrznych jest procesem bardzo powolnym i czasochłonnym, ponieważ musimy wziąć pod uwagę również dziecko usuniętego klucza. | Usuwanie w drzewie B+ jest bardzo szybkie, ponieważ wszystkie rekordy przechowywane są w węzłach-liście, więc nie musimy brać pod uwagę dziecka węzła. |
| W Btree dostęp sekwencyjny nie jest możliwy. | W drzewie B+ wszystkie węzły liści są połączone ze sobą za pomocą wskaźnika, dzięki czemu możliwy jest dostęp sekwencyjny. |
| W Btree wykonywana jest większa liczba operacji podziału, przez co wysokość wzrasta w porównaniu do szerokości, | Drzewo B+ ma większą szerokość w porównaniu do wysokości. |
| W Btree każdy węzeł ma co najmniej dwie gałęzie i każdy węzeł zawiera pewne rekordy, więc nie musimy przechodzić do węzłów liści, aby uzyskać dane. | W drzewie B+ węzły wewnętrzne zawierają tylko wskaźniki, a węzły liści zawierają rekordy. Wszystkie węzły liściowe znajdują się na tym samym poziomie, więc aby uzyskać dane, musimy przejść do węzłów liściowych. |
| Węzeł główny zawiera co najmniej 2 do m dzieci, gdzie m jest porządkiem drzewa. | Węzeł główny zawiera co najmniej 2 do m dzieci, gdzie m jest porządkiem drzewa. |
