The Szary kod to ciąg binarnych systemów liczbowych, znany również jako odzwierciedlony kod binarny . Powodem nazywania tego kodu odzwierciedlonym kodem binarnym jest porównanie pierwszych wartości N/2 z ostatnimi wartościami N/2 w odwrotnej kolejności. W tym kodzie dwie kolejne wartości różnią się jednym bitem cyfr binarnych. Kody Graya są używane w ogólnej sekwencji liczb binarnych generowanych sprzętowo. Liczby te powodują niejasności lub błędy przy przejściu z jednej liczby na kolejną. Ten kod po prostu rozwiązuje ten problem, zmieniając tylko jeden bit, gdy następuje przejście między liczbami.
Szary kod jest kodem bardzo lekkim, ponieważ nie zależy od wartości cyfry określonej przez pozycję. Kod ten nazywany jest także kodem zmiennej cyklicznej, ponieważ przejście jednej wartości do kolejnej wartości niesie ze sobą zmianę tylko jednego bitu.
Jak wygenerować kod Graya?
Metody przedrostka i metody odzwierciedlania są rekurencyjnie używane do generowania kodu Graya liczby. Do generowania szarego kodu:
- Znajdujemy liczbę bitów wymaganych do przedstawienia liczby.
- Następnie znajdujemy kod dla 0, tj. 0000, który jest taki sam jak binarny.
- Teraz bierzemy poprzedni kod, tj. 0000, i zmieniamy jego najbardziej znaczący fragment.
- Wykonujemy ten proces w sposób wyłączny, dopóki wszystkie kody nie zostaną jednoznacznie zidentyfikowane.
- Jeśli zmieniając najbardziej znaczący bit, znajdziemy ten sam kod, który otrzymaliśmy wcześniej, to drugi najbardziej znaczący bit zostanie zmieniony i tak dalej.
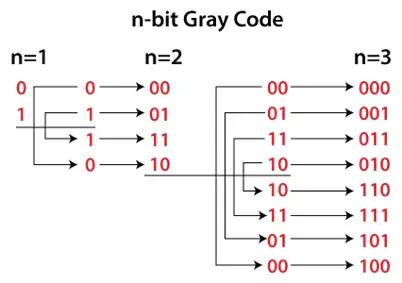
Proces generowania Gray Code

Tabela szarego kodu
| Liczba dziesiętna | Liczba binarna | Szary kod |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| jedenaście | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| piętnaście | 1111 | 1000 |
