Wstęp:

Półsumator to cyfrowy obwód logiczny, który wykonuje binarne dodawanie dwóch jednobitowych liczb binarnych. Posiada dwa wejścia A i B oraz dwa wyjścia SUM i CARRY. Wynik SUM to najmniej znaczący bit (LSB) wyniku, podczas gdy wynik CARRY to najbardziej znaczący bit (MSB) wyniku, wskazujący, czy nastąpiło przeniesienie z dodania dwóch wejść. Półsumator można zaimplementować przy użyciu podstawowych bramek, takich jak bramki XOR i AND.

Jasne, oto bardziej szczegółowe wyjaśnienie obwodu półsumatora:

Półsumator jest podstawowym elementem składowym bardziej złożonych obwodów sumatorów, takich jak sumatory pełne i sumatory wielobitowe. Wykonuje binarne dodawanie dwóch jednobitowych wejść A i B i zapewnia dwa wyjścia, SUM i CARRY.

stdin w c

Wyjście SUM to najmniej znaczący bit (LSB) wyniku, który jest XOR dwóch wejść A i B. Bramka XOR realizuje operację dodawania cyfr binarnych, gdzie 1 jest generowana na wyjściu SUM tylko wtedy, gdy wejść wynosi 1.

Wyjście CARRY jest najbardziej znaczącym bitem (MSB) wyniku, wskazującym, czy nastąpiło przeniesienie z dodania dwóch wejść. Wyjście CARRY to AND dwóch wejść A i B. Bramka AND generuje 1 na wyjściu CARRY tylko wtedy, gdy oba wejścia mają wartość 1.

Półsumator (HA):

Półsumator jest najprostszym ze wszystkich obwodów sumatora. Półsumator to kombinacyjny obwód arytmetyczny, który dodaje dwie liczby i generuje bity sumy i bit przeniesienia (c) jako dane wyjściowe. Dodanie 2 bitów odbywa się za pomocą obwodu kombinowanego zwanego sumatorem pół. Zmienne wejściowe to bity augend i addend, a zmienne wyjściowe to bity sumy i przeniesienia. A i B to dwa bity wejściowe.

rozważmy dwa bity wejściowe A i B, następnie bity sumy to X-OR A i B. Z funkcji półsumatora wynika, że ​​wymaga on jednej bramki X-OR i jednej bramki AND budowa.

Tabela prawdy:

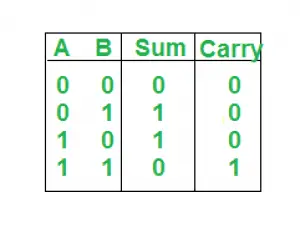
Tutaj wykonujemy dwie operacje Sum i Carry, dlatego potrzebujemy dwóch map K, po jednej dla każdej z nich, aby wyprowadzić wyrażenie.

Wyrażenie logiczne:

Dla sumy:

wyliczenia Java

Suma = A XOR B

Do przenoszenia:

Przenoszenie = A I B

Realizacja:

Notatka: Półsumator ma tylko dwa wejścia i nie ma możliwości dodania przeniesienia pochodzącego z bitów niższego rzędu, gdy wykonywane jest dodawanie wielokrotne.

Zalety i wady półsumatora w logice cyfrowej:

Zalety półsumatora w logice cyfrowej:

1. Prostota: Pół-viper to prosty obwód, który wymaga kilku podstawowych części, takich jak XOR ORAZ wejścia. Nie jest to trudne do przeprowadzenia i można je wykorzystać w wielu zaawansowanych frameworkach.

2. Prędkość: Pół żmija działa niezwykle szybko, co czyni go rozsądnym do stosowania w szybkich obwodach skomputeryzowanych.

Wady półsumatora w logice cyfrowej:

1.Ograniczona użyteczność: Pół żmija może dodać dwie jednoczęściowe liczby i wygenerować sumę i bit przekazujący. Nie może wykonywać rozszerzania liczb wielobitowych, co wymaga użycia dodatkowych skomplikowanych obwodów, takich jak pełne sumatory.

2. Brak informacji o przekazywaniu: Półwąż nie ma sygnału wejściowego, co ogranicza jego wartość w przypadku bardziej zadziwiających zadań związanych z rozszerzaniem. Wejście przekazujące jest ważne, aby przeprowadzić ekspansję liczb wielobitowych i połączyć ze sobą wiele sumatorów.

wiersz i kolumna

3. Odroczenie rozmnażania: Obwód półwęża ma opóźnienie proliferacji, czyli czas potrzebny na zmianę wyniku w świetle dostosowania informacji. Może to powodować problemy z synchronizacją w obwodach skomputeryzowanych, szczególnie w szybkich strukturach.

Zastosowanie półsumatora w logice cyfrowej:

1.Obwody arytmetyczne: Półsumatory są wykorzystywane w obwodach przetwarzających liczby w celu dodawania liczb podwójnych. W momencie, gdy w łańcuchu są powiązane różne półsumatory, mogą one dodawać wielobitowe liczby podwójne.

2.Przetwarzanie danych: Półsumatory są wykorzystywane w aplikacjach do obsługi informacji, takich jak skomputeryzowana obsługa sygnałów, szyfrowanie informacji i korygowanie błędów.

3. Rozwikłanie problemu: W zarządzaniu pamięcią półsumatory są wykorzystywane w obwodach odszyfrowywania adresów w celu określenia lokalizacji określonego obszaru pamięci.

4. Obwody kodera i dekodera: Półsumatory są wykorzystywane w obwodach kodera i dekodera w skomputeryzowanych ramach korespondencji.

5.Multipleksery i demultipleksery: Półsumatory są wykorzystywane w multiplekserach i demultiplekserach do wybierania i przekazywania informacji.

6.Liczniki: W licznikach stosuje się półsumatory, aby zwiększyć liczbę o jeden.