W tym artykule omówimy sposób zaokrąglania liczb w Pythonie za pomocą odpowiednich metod i przykładów Jak zaokrąglić Pyton .
Przykład:
Input: 3.5 Output: 4 Explanation: Nearest whole number. Input: 3.74 Output: 3.7 Explanation: Rounded to one decimal place.>
Zaokrąglaj liczby w Pythonie
Zaokrąglanie liczby oznacza uproszczenie liczby poprzez zachowanie jej wartości w stanie nienaruszonym, ale bliżej następnej liczby. Istnieją różne metody zaokrąglania liczb w Pythonie, tutaj omawiamy niektóre powszechnie stosowane Jak zaokrąglić w Pythonie Poniżej znajdują się następujące punkty, które zostaną omówione w tym artykule przy użyciu języka Python:
- Korzystanie z wbudowanej funkcji round().
- Za pomocą Obcięcie pojęcie
- Za pomocą Matematyka.ceil() I Podłoga matematyczna() Funkcje
- Za pomocą matematyka.ceil
- Za pomocą matematyka.podłoga
- Używając
numpy>Moduł - Używając Zaokrąglanie Koncepcja stronniczości
- Zaokrąglanie do połowy od zera w Pythonie
Okrągłe liczby w Pythonie u śpiewać Wbudowany okrągły() Funkcjonować
W Pythonie jest to wbudowane funkcja round(). która zaokrągla liczbę do podanej liczby cyfr. Funkcja round() przyjmuje dwa argumenty numeryczne, n i n cyfr, a następnie zwraca liczbę n po zaokrągleniu jej do n cyfr. Jeżeli liczba cyfr nie jest przewidziana do zaokrąglenia, funkcja zaokrągla podaną liczbę n do najbliższej liczby całkowitej.
harmonogram okrężny
Przykład : W tym przykładzie poniższy kod ilustruje funkcję „round()” dla liczb całkowitych i zmiennoprzecinkowych. Ilustruje również zaokrąglanie do dwóch miejsc po przecinku, pokazując przypadki, w których następna cyfra to 5, większa niż 5 i mniejsza niż 5.
Python3
# For integers> print>(>round>(>11>))> # For floating point> print>(>round>(>22.7>))> # if the second parameter is present> # when the (ndigit+1)th digit is =5> print>(>round>(>4.465>,>2>))> > # when the (ndigit+1)th digit is>=5> print>(>round>(>4.476>,>2>))> > # when the (ndigit+1)th digit is <5> print>(>round>(>4.473>,>2>))> |
>
>
Wyjście:
11 23 4.46 4.48 4.47>
Okrągłe liczby w Pythonie u śpiewać Obcięcie pojęcie
W tej funkcji każda cyfra po danej pozycji jest zastępowana przez 0. python ścięty() funkcjonować można używać z liczbami dodatnimi i ujemnymi. Funkcję obcinania można zaimplementować w następujący sposób:
- Mnożąc liczbę przez 10^p (10 podniesione do ptpotęga), aby przesunąć przecinek dziesiętny p miejsc w prawo.
- Biorąc część całkowitą tej nowej liczby za pomocą int().
- Przesunięcie miejsca dziesiętnego p umieszcza się z powrotem w lewo, dzieląc przez 10^p.
Python3
# defining truncate function> # second argument defaults to 0> # so that if no argument is passed> # it returns the integer part of number> def> truncate(n, decimals>=> 0>):> >multiplier>=> 10> *>*> decimals> >return> int>(n>*> multiplier)>/> multiplier> print>(truncate(>16.5>))> print>(truncate(>->3.853>,>1>))> print>(truncate(>3.815>,>2>))> # we can truncate digits towards the left of the decimal point> # by passing a negative number.> print>(truncate(>346.8>,>->1>))> print>(truncate(>->2947.48>,>->3>))> |
>
>
Wyjście:
16.0 -3.8 3.81 340.0 -2000.0>
Okrągłe liczby w Pythonie u śpiewać Matematyka.ceil() I Podłoga matematyczna() Funkcje
Matematyka . stropować() : Ta funkcja zwraca najbliższą liczbę całkowitą większą lub równą podanej liczbie.
Podłoga matematyczna() : Ta funkcja zwraca najbliższą liczbę całkowitą mniejszą lub równą podanej liczbie.
Przykład :W tym przykładzie poniższy kod wykorzystuje bibliotekę `math` do obliczenia wartości górnych dla dodatnich i ujemnych miejsc dziesiętnych za pomocą `math.ceil` i wartości minimalnych za pomocą `math.floor`. Dane wyjściowe to 5, 0, 2 i -1 dla odpowiednich przypadków.
Python3
# import math library> import> math> # ceil value for positive> # decimal number> print>(math.ceil(>4.2>))> # ceil value for negative> # decimal number> print>(math.ceil(>->0.5>))> # floor value for decimal> # and negative number> print>(math.floor(>2.2>))> print>(math.floor(>->0.5>))> |
>
>
Wyjście:
5 0 2 -1>
Okrągłe liczby w Pythonie u śpiewaj math.ceil
Zaokrąglanie liczby polega na przesunięciu przecinka w prawo, zaokrągleniu w górę, a następnie przesunięciu go z powrotem w lewo w celu uzyskania precyzji za pomocą ` matematyka.ceil() ` i operacje mnożenia/dzielenie.
Przykład :W tym przykładzie poniższy kod definiuje funkcję `round_up` przy użyciu biblioteki `math`, która zaokrągla liczbę do określonego miejsca dziesiętnego. Wykorzystuje mnożenie, zaokrąglanie za pomocą funkcji „math.ceil()” i dzielenie w celu zapewnienia precyzji. Wartości dodatnie i ujemne są testowane pod kątem zaokrąglania.
Python3
# import math library> import> math> # define a function for> # round_up> def> round_up(n, decimals>=> 0>):> >multiplier>=> 10> *>*> decimals> >return> math.ceil(n>*> multiplier)>/> multiplier> # passing positive values> print>(round_up(>2.1>))> print>(round_up(>2.23>,>1>))> print>(round_up(>2.543>,>2>))> # passing negative values> print>(round_up(>22.45>,>->1>))> print>(round_up(>2352>,>->2>))> |
>
>
Wyjście:
3.0 2.3 2.55 30.0 2400.0>
Możemy postępować zgodnie z poniższym diagramem, aby zrozumieć zaokrąglanie w górę i w dół. Zaokrąglaj w górę w prawo i w dół w lewo.
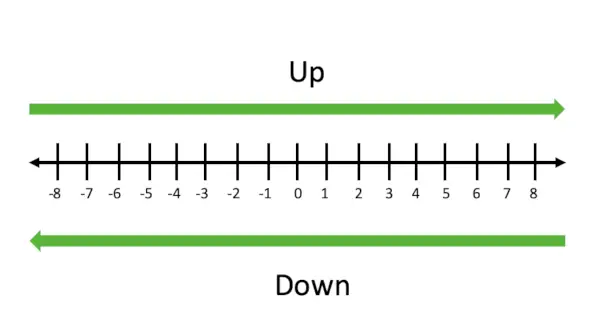
Zaokrąglanie w górę zawsze zaokrągla liczbę w prawo na osi liczbowej, a zaokrąglanie w dół zawsze zaokrągla liczbę w lewo na osi liczbowej.
Okrągłe liczby w Pythonie u śpiewać matematyka.podłoga
W trybie Zaokrąglanie w dół liczba jest zaokrąglana w dół do określonej liczby cyfr. Funkcję zaokrąglania w dół można zaimplementować w następujący sposób:
- Najpierw przecinek dziesiętny w n przesuwa się o odpowiednią liczbę miejsc w prawo, mnożąc n przez 10** miejsc po przecinku.
- Nowa wartość jest zaokrąglana w górę do najbliższej liczby całkowitej przy użyciu matematyka.podłoga() .
- Na koniec przecinek dziesiętny przesuwa się z powrotem w lewo, dzieląc przez 10 ** miejsc po przecinku.
Python3
import> math> # defining a function for> # round down.> def> round_down(n, decimals>=>0>):> >multiplier>=> 10> *>*> decimals> >return> math.floor(n>*> multiplier)>/> multiplier> # passing different values to function> print>(round_down(>2.5>))> print>(round_down(>2.48>,>1>))> print>(round_down(>->0.5>))> |
>
>
Wyjście:
2.0 2.4 -1.0>
Okrągłe liczby w Pythonie u śpiewaj moduł Numpy
Moduł NumPy w Pythonie zapewnia numpy.round()>funkcjonować zaokrąglać liczby. Ta funkcja zaokrągla każdy element tablicy do najbliższej liczby całkowitej lub określonej liczby miejsc po przecinku.
Przykład : W tym przykładzie poniższy kod wykorzystuje moduł NumPy do utworzenia tablicy „arr” i zaokrągla każdy element do najbliższej liczby całkowitej („zaokrąglone_integers”) i do dwóch miejsc po przecinku („zaokrąglone_dziesiętne”). Wyniki są następnie drukowane w celu wyświetlenia.
Python3
import> numpy as np> # Creating an array> arr>=> np.array([>1.234>,>2.567>,>3.789>])> # Rounding each element to the nearest integer> rounded_integers>=> np.>round>(arr)> # Rounding each element to two decimal places> rounded_decimals>=> np.>round>(arr, decimals>=>2>)> # Displaying the results> print>(>'Nearest integer:'>, rounded_integers)> print>(>'Decimal places:'>, rounded_decimals)> |
>
>
Wyjście :
Nearest integer: [1. 3. 4.] Decimal places: [1.23 2.57 3.79]>
Okrągłe liczby w Pythonie u śpiewać Zaokrąglanie pojęcie.
Koncepcja symetrii wprowadza pojęcie błędu zaokrąglania, które opisuje, jak zaokrąglenie wpływa na dane liczbowe w zbiorze danych.
Strategia zaokrąglania w górę ma tendencję do zaokrąglania w kierunku dodatniej nieskończoności, ponieważ wartość jest zawsze zaokrąglana w górę w kierunku dodatniej nieskończoności. Podobnie strategia zaokrąglania w dół ma tendencję do zaokrąglania w kierunku ujemnej nieskończoności. Strategia obcinania obejmuje odchylenie w kierunku ujemnej nieskończoności w przypadku wartości dodatnich i zaokrąglenie w kierunku dodatniej nieskończoności w przypadku wartości ujemnych. Ogólnie mówi się, że funkcje zaokrąglające charakteryzujące się tym zachowaniem mają zaokrąglenie w stronę zera.
a) Zaokrąglanie w górę koncepcja w Pythonie
Zaokrąglanie w górę zaokrągla każdą liczbę do najbliższej liczby z określoną precyzją i przerywa remisy poprzez zaokrąglenie w górę.
Strategia zaokrąglania o połowę w górę realizowana jest poprzez przesunięcie przecinka w prawo o żądaną liczbę miejsc. W tym przypadku będziemy musieli ustalić, czy cyfra po przesuniętym przecinku jest mniejsza czy większa od równej 5.
Do przesuniętej wartości możemy dodać 0,5, a następnie zaokrąglić ją w dół za pomocą funkcji math.floor().
Implementacja funkcji round_half_up():
Przykład: W tym przykładzie poniższy kod definiuje `round_half_up`, niestandardową funkcję zaokrąglania wykorzystującą metodę zaokrąglania o połowę w górę z `math.floor()` dla zapewnienia precyzji. Prezentacje obejmują liczby dodatnie i ujemne z różnymi miejscami po przecinku.
Python3
import> math> # defining round_half_up> def> round_half_up(n, decimals>=>0>):> >multiplier>=> 10> *>*> decimals> >return> math.floor(n>*> multiplier>+> 0.5>)>/> multiplier> # passing different values to the function> print>(round_half_up(>1.28>,>1>))> print>(round_half_up(>->1.5>))> print>(round_half_up(>->1.225>,>2>))> |
>
>
Wyjście:
1.3 -1.0 -1.23>
b) Zaokrąglanie w dół koncepcja w Pythonie
Zaokrągla to do najbliższej liczby, podobnie jak metoda zaokrąglania o połowę w górę, z tą różnicą, że remisuje poprzez zaokrąglenie do mniejszej z dwóch liczb. Strategię zaokrąglania o połowę w dół implementuje się poprzez zastąpienie funkcji math.floor() w funkcji round_half_up() funkcją math.ceil(), a następnie odejmowanie 0,5 zamiast dodawania.
Implementacja funkcji round_half_down():
W tym przykładzie poniższy kod definiuje `round_half_down` przy użyciu biblioteki `math` w celu uzyskania zachowania zaokrąglenia do połowy w dół. Wykorzystuje mnożenie, odejmowanie i funkcję „math.ceil()” do zaokrąglania do zera. Przypadki testowe obejmują dodatnie i ujemne miejsca po przecinku, zaokrąglone do jednego miejsca po przecinku.
Python3
# import math library> import> math> # defining a function> # for round_half_down> def> round_half_down(n, decimals>=>0>):> >multiplier>=> 10> *>*> decimals> >return> math.ceil(n>*> multiplier>-> 0.5>)>/> multiplier> # passing different values to the function> print>(round_half_down(>2.5>))> print>(round_half_down(>->2.5>))> print>(round_half_down(>2.25>,>1>))> |
>
>
Wyjście:
2.0 -3.0 2.2>
Zaokrąglanie do połowy od zera w Pythonie
Zaokrąglanie o połowę od zera musimy zacząć jak zwykle od przesunięcia przecinka w prawo o określoną liczbę miejsc, a następnie zwrócić uwagę na cyfrę (d) znajdującą się bezpośrednio na prawo od miejsca dziesiętnego w nowej liczbie. Należy rozważyć cztery przypadki:
- Jeśli n jest dodatnie i d>= 5, zaokrąglij w górę
- Jeśli n jest dodatnie i d = 5, zaokrąglij w dół
- Jeśli n jest ujemne, a d>= 5, zaokrąglij w dół
- Jeśli n jest ujemne, a d <5, zaokrąglij w górę
Po zaokrągleniu zgodnie z powyższymi zasadami możemy przesunąć przecinek z powrotem w lewo.
- Zaokrąglanie od połowy do parzystej: Istnieje sposób na złagodzenie błędu zaokrąglania podczas zaokrąglania wartości w zbiorze danych. Możemy po prostu zaokrąglić remisy do najbliższej liczby parzystej z żądaną precyzją. Strategia zaokrąglania od połowy do parzystej to strategia używana przez wbudowaną w Pythonie funkcję round(). The klasa dziesiętna zapewnia obsługę szybkiej, poprawnie zaokrąglonej dziesiętnej arytmetyki zmiennoprzecinkowej. Daje to kilka korzyści w porównaniu z typem danych float. Domyślna strategia zaokrąglania w module dziesiętnym to ROUND_HALF_EVEN.
Przykład: W tym przykładzie poniższy kod wykorzystuje funkcję „Decimal” z biblioteki „decimal” do dokładnego przedstawienia liczb dziesiętnych. Kontrastuje to z tworzeniem obiektu „Decimal” z łańcucha i bezpośrednio z liczby zmiennoprzecinkowej. Następnie do zaokrąglania do określonych miejsc dziesiętnych wykorzystywana jest funkcja „quantize()”, co pozwala wykazać precyzję w arytmetyce dziesiętnej.
Python3
# import Decimal function from> # decimal library> from> decimal>import> Decimal> print>(Decimal(>'0.1'>))> print>(Decimal(>0.1>))> # Rounding a Decimal number is> # done with the .quantize() function> # '1.0' in .quantize() determines the> # number of decimal places to round the number> print>(Decimal(>'1.65'>).quantize(Decimal(>'1.0'>)))> print>(Decimal(>'1.675'>).quantize(Decimal(>'1.00'>)))> |
>
>
Wyjście:
0.1 0.1000000000000000055511151231257827021181583404541015625 1.6 1.68>
