Świat algorytmów jest piękny, z różnorodnymi strategiami i narzędziami rozwijanymi przez całą dobę, aby zaspokoić zapotrzebowanie na obliczenia o wysokiej wydajności. Rzeczywiście, gdy algorytmy inspirowane są prawami natury, obserwuje się ciekawe wyniki. Do takiej klasy algorytmów należą algorytmy ewolucyjne. Algorytmy te zaprojektowano tak, aby naśladować określone zachowania i cechy ewolucyjne ludzkiego genomu. Co więcej, taki projekt algorytmiczny nie jest ograniczony tylko do ludzi, ale może być również inspirowany naturalnym zachowaniem niektórych zwierząt. Podstawowym celem tworzenia takich metodologii jest zapewnienie realistycznych, odpowiednich, a jednocześnie niedrogich rozwiązań problemów, których dotychczas nie da się rozwiązać konwencjonalnymi środkami.

W ten sposób ewoluowały różne techniki optymalizacji w oparciu o takie algorytmy ewolucyjne, otwierając w ten sposób dziedzinę metaheurystyki. Metaheurystyczny pochodzi od dwóch greckich słów, a mianowicie: Meta oznaczający jeden poziom wyżej I heuryskeina oznaczający znaleźć . Algorytmy takie jak optymalizacja roju cząstek (PSO) i optymalizacja kolonii mrówek (ACO) są przykładami inteligencji roju i metaheurystyki. Celem inteligencji roju jest projektowanie inteligentnych systemów wieloagentowych poprzez czerpanie inspiracji ze zbiorowego zachowania owadów społecznych, takich jak mrówki, termity, pszczoły, osy i innych społeczności zwierzęcych, takich jak stada ptaków lub ławice ryb.

Tło:

Technika optymalizacji kolonii mrówek jest wyłącznie inspirowana plądrowanie zachowanie kolonii mrówek, po raz pierwszy wprowadzone przez Marco Dorigo w latach 90. XX wieku. Mrówki to owady eusocial, które wolą przetrwanie i utrzymanie się w społeczności, niż jako pojedynczy gatunek. Komunikują się ze sobą za pomocą dźwięku, dotyku i feromonów. Feromony to organiczne związki chemiczne wydzielane przez mrówki, które wywołują reakcję społeczną u przedstawicieli tego samego gatunku. Są to substancje chemiczne, które mogą działać jak hormony poza organizmem wydzielającej osoby i wpływać na zachowanie osób otrzymujących. Ponieważ większość mrówek żyje na ziemi, wykorzystują powierzchnię gleby do pozostawiania śladów feromonów, za którymi mogą podążać (wąchać) inne mrówki.
Mrówki żyją w gniazdach zbiorowych, a podstawową zasadą ACO jest obserwacja ruchu mrówek z gniazd w celu poszukiwania pożywienia najkrótszą możliwą drogą. Początkowo mrówki zaczynają poruszać się losowo w poszukiwaniu pożywienia wokół swoich gniazd. To losowe wyszukiwanie otwiera wiele dróg od gniazda do źródła pożywienia. Teraz, w zależności od jakości i ilości pożywienia, mrówki niosą w drodze powrotnej część pożywienia z niezbędnym stężeniem feromonów. W zależności od tych prób feromonów prawdopodobieństwo wyboru określonej ścieżki przez następujące mrówki byłoby czynnikiem prowadzącym do źródła pożywienia. Najwyraźniej prawdopodobieństwo to opiera się na stężeniu i szybkości parowania feromonu. Można również zaobserwować, że ponieważ szybkość parowania feromonu jest również czynnikiem decydującym, długość każdej ścieżki można łatwo obliczyć.

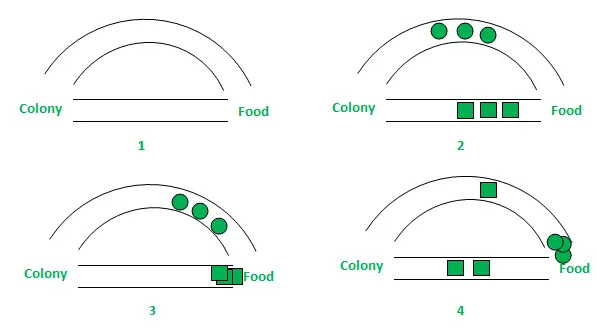
Dla uproszczenia na powyższym rysunku wzięto pod uwagę tylko dwie możliwe ścieżki między źródłem pożywienia a gniazdem mrówek. Etapy można analizować w następujący sposób:

Etap 1: Wszystkie mrówki są w swoim gnieździe. W środowisku nie występuje zawartość feromonów. (W przypadku projektowania algorytmicznego można uwzględnić resztkową ilość feromonów bez zakłócania prawdopodobieństwa) Etap 2: Mrówki rozpoczynają poszukiwania z równym (0,5) prawdopodobieństwem wzdłuż każdej ścieżki. Jest oczywiste, że zakrzywiona ścieżka jest dłuższa, dlatego też czas potrzebny mrówkom na dotarcie do źródła pożywienia jest dłuższy niż w przypadku drugiej. Etap 3: Mrówki krótszą ścieżką wcześniej docierają do źródła pożywienia. Teraz najwyraźniej stoją przed podobnym dylematem selekcyjnym, ale tym razem ze względu na ślad feromonowy wzdłuż dostępnej już krótszej ścieżki, prawdopodobieństwo selekcji jest większe. Etap 4: Więcej mrówek powraca krótszą drogą, w wyniku czego wzrasta również stężenie feromonów. Ponadto na skutek parowania zmniejsza się stężenie feromonów na dłuższej ścieżce, zmniejszając prawdopodobieństwo wyboru tej ścieżki w dalszych etapach. Dlatego cała kolonia stopniowo korzysta z krótszej ścieżki z większym prawdopodobieństwem. Zatem optymalizacja ścieżki została osiągnięta.

Projekt algorytmiczny:

Na podstawie powyższego zachowania mrówek można teraz opracować projekt algorytmiczny. Dla uproszczenia rozważono pojedyncze źródło pożywienia i pojedynczą kolonię mrówek z zaledwie dwiema możliwymi ścieżkami przemieszczania się. Cały scenariusz można zrealizować za pomocą grafów ważonych, w których kolonia mrówek i źródło pożywienia pełnią rolę wierzchołków (lub węzłów); ścieżki służą jako krawędzie, a wartości feromonów to wagi powiązane z krawędziami.
Niech będzie wykres G = (V, E) gdzie V, E są krawędziami i wierzchołkami grafu. Wierzchołki według naszych rozważań są W_S (Wierzchołek źródłowy – kolonia mrówek) i W_D (Wierzchołek docelowy – źródło pożywienia). Obie krawędzie są I₁ I I₂ z długościami L₁ I L₂ przypisany każdemu. Można teraz założyć, że powiązane wartości feromonów (wskazujące ich siłę) są takie R₁ I R₂ dla wierzchołków E₁i E₂odpowiednio. Zatem dla każdej mrówki początkowe prawdopodobieństwo wyboru ścieżki (pomiędzy E₁i E₂) można wyrazić w następujący sposób:

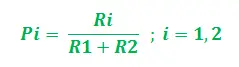
Widocznie, jeśli R₁>R₂, prawdopodobieństwo wyboru E₁jest wyższa i odwrotnie. Teraz, wracając tą najkrótszą drogą, powiedz E_I, wartość feromonu jest aktualizowana dla odpowiedniej ścieżki. Aktualizacja odbywa się na podstawie długości ścieżek oraz szybkości parowania feromonów. Zatem aktualizację można przeprowadzić etapowo w następujący sposób:

W zależności od długości ścieżki –

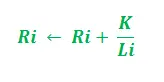
W powyższej aktualizacji i = 1, 2 i „K” służą jako parametr modelu. Ponadto aktualizacja jest zależna od długości ścieżki. Krótsza droga, wyższy dodany feromon. Zgodnie z szybkością parowania feromonu –

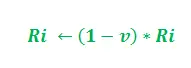
Parametr „v” należy do przedziału (0, 1] regulującego parowanie feromonów. Dalej i = 1, 2.

W każdej iteracji wszystkie mrówki są umieszczane w wierzchołku źródłowym V_S(Kolonia mrówek). Następnie mrówki przemieszczają się z V_Sdo V_D(źródło pożywienia) po kroku 1. Następnie wszystkie mrówki wyruszają w podróż powrotną i wzmacniają wybraną przez siebie ścieżkę w oparciu o krok 2.

Pseudo kod:

 Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>

Aktualizację feromonów i obliczenia sprawności w powyższym pseudokodzie można znaleźć poprzez etapowe implementacje wspomniane powyżej.
Tym samym ustalono wprowadzenie techniki optymalizacji ACO. Zastosowanie ACO można rozszerzyć na różne problemy, takie jak słynne TSP (problem komiwojażera) .

Bibliografia:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf