Wartość arytmetyczna używana do reprezentowania ilości i używana do wykonywania obliczeń jest zdefiniowana jako Liczby. Symbole takie jak 4, 5, 6, które reprezentują liczbę, nazywane są cyframi. Bez liczb nie możemy liczyć rzeczy, dat, godzin, pieniędzy itp. Liczby te służą również do pomiaru i służą do etykietowania.

Właściwości liczb sprawiają, że są one pomocne w wykonywaniu na nich operacji arytmetycznych. Liczby te można zapisać w formie liczbowej, a także słownie.

Na przykład , 3 zapisuje się słownie jako trzy, 35 zapisuje się słownie jako trzydzieści pięć itd. Aby dowiedzieć się więcej, uczniowie mogą zapisać słownie liczby od 1 do 100.

Istnieją różne rodzaje liczb, których możemy się nauczyć. Są to liczby całkowite i naturalne, nieparzyste i parzyste, wymierne i niewymierne itp.

Co to jest system liczbowy?

System liczbowy to metoda przedstawiania liczb za pomocą pisma, która jest matematycznym sposobem przedstawiania liczb z danego zbioru poprzez użycie liczb lub symboli w sposób matematyczny. System pisma służący do oznaczania liczb za pomocą cyfr lub symboli w logiczny sposób definiuje się jako system liczbowy.

Do tworzenia wszystkich liczb możemy używać cyfr od 0 do 9. Za pomocą tych cyfr każdy może stworzyć nieskończone liczby.

Na przykład 156, 3907, 3456, 1298, 784859 itd.

Co to jest pierwiastek kwadratowy?

Wartość liczby pierwiastków kwadratowych, która po pomnożeniu sama w sobie daje liczbę pierwotną. Załóżmy, że a jest pierwiastkiem kwadratowym z b, wówczas jest reprezentowane jako a = √b lub możemy wyrazić to samo równanie jako a2 = b. Tutaj „√” ten symbol, którego użyliśmy do przedstawienia pierwiastka liczb, jest określany jako radykalny. Liczba dodatnia, która ma zostać pomnożona przez samą siebie, reprezentuje kwadrat liczby. Pierwiastek kwadratowy z dowolnej liczby dodatniej daje liczbę pierwotną.

Na przykład, kwadrat liczby 4 wynosi 16, 4²= 16 i pierwiastek kwadratowy z 16, √16 = 4. Ponieważ 4 jest kwadratem doskonałym, łatwo jest znaleźć pierwiastek kwadratowy z takich liczb, ale w przypadku niedoskonałego kwadratu jest to naprawdę trudne.

Pierwiastek kwadratowy jest reprezentowany jako „√” Nazywa się to symbolem radykalnym. Aby przedstawić liczbę jako pierwiastek kwadratowy, za pomocą tego symbolu można zapisać jako: „√a”, gdzie a jest liczbą.

cpp równa się

Liczba znajdująca się pod symbolem pierwiastka nazywana jest radykandą. Na przykład pierwiastek kwadratowy z 4 jest również przedstawiany jako pierwiastek z 4. Obydwa reprezentują tę samą wartość.

Wzór na znalezienie pierwiastka kwadratowego to: a = √b

Właściwości pierwiastków kwadratowych

Jest ona zdefiniowana jako funkcja jeden do jednego, która jako dane wejściowe przyjmuje liczbę dodatnią i zwraca pierwiastek kwadratowy z podanej liczby wejściowej.

f(x) = √x

Na przykład tutaj, jeśli x = 9, funkcja zwraca wartość wyjściową jako 3.

Właściwości pierwiastka kwadratowego są następujące:

Acore procesu Androida ciągle się zatrzymuje

• Jeśli liczba jest liczbą doskonałą kwadratową, to na pewno istnieje doskonały pierwiastek kwadratowy.
• Jeśli liczba kończy się parzystą liczbą zer (0), wówczas możemy otrzymać pierwiastek kwadratowy.
• Obie wartości pierwiastka kwadratowego można pomnożyć. Na przykład √3 można pomnożyć przez √2, wówczas wynikiem będzie √6.
• Kiedy mnoży się dwa takie same pierwiastki kwadratowe, wynik musi być liczbą pierwiastkową. Pokazuje, że wynikiem jest liczba niebędąca pierwiastkiem kwadratowym. Na przykład, gdy √7 zostanie pomnożone przez √7, otrzymany wynik wyniesie 7.
• Pierwiastek kwadratowy z liczb ujemnych jest nieokreślony. Zatem idealny kwadrat nie może być liczbą ujemną.
• Niektóre liczby kończą się na 2, 3, 7 lub 8 (w cyfrze jedności), wtedy doskonały pierwiastek kwadratowy nie istnieje.
• Niektóre liczby kończą się cyfrą jedności na 1, 4, 5, 6 lub 9, wówczas liczba będzie pierwiastkiem kwadratowym.

Znalezienie pierwiastka kwadratowego z liczby będącej idealnym kwadratem jest łatwe.

Idealne kwadraty to liczby dodatnie, które można zapisać jako pomnożenie liczby przez nią samą, lub można powiedzieć, że idealny kwadrat to liczba będąca potęgą 2 dowolnej liczby całkowitej.

Liczba, którą można wyrazić jako iloczyn dwóch równych liczb całkowitych. Na przykład 16 jest idealnym kwadratem, ponieważ jest iloczynem dwóch równych liczb całkowitych, 4 × 4 = 16. Jednak 24 nie jest idealnym kwadratem, ponieważ nie można go wyrazić jako iloczynu dwóch równych liczb całkowitych. (8 × 3 = 24).

Liczbę otrzymaną przez podniesienie liczby całkowitej do kwadratu nazywamy kwadratem doskonałym.

Jeśli założymy, że N jest idealnym kwadratem liczby całkowitej y, można to zapisać jako N = iloczyn y i y = y².

Zatem idealny wzór kwadratowy można wyrazić jako:

N = T ²

Użyjmy formuły z wartościami:

Jeśli y = 9 i N = y²

Oznacza to, N = 9²= 81.

Tutaj 81 jest idealnym kwadratem liczby 9, ponieważ jest kwadratem liczby całkowitej.

czcionka lateksowa

Za pomocą pierwiastków kwadratowych możemy określić, czy liczba jest doskonała kwadratowa, czy nie, jeśli obliczymy pierwiastek kwadratowy z danej liczby.

Jeśli pierwiastek kwadratowy jest liczbą całkowitą, to dana liczba będzie liczbą doskonałą, a jeśli wartość pierwiastka kwadratowego nie jest liczbą całkowitą, to dana liczba nie jest liczbą idealną.

Na przykład, aby sprawdzić, czy 24 jest idealnym kwadratem, czy nie, obliczymy jego pierwiastek kwadratowy. √24 = 4,898979. Jak widzimy, 4,898979 nie jest liczbą całkowitą, więc 24 nie jest idealnym kwadratem.

Weźmy inny przykład

Liczba 49. √49 = 7. Widzimy, że 7 jest liczbą całkowitą, zatem 49 jest idealnym kwadratem.

Czy 196 to idealny kwadrat?

Rozwiązanie:

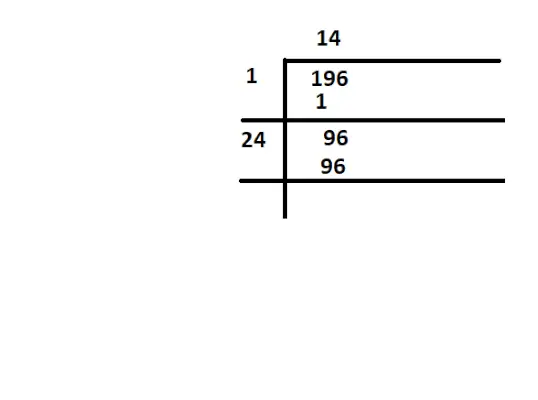
Aby sprawdzić, czy 196 jest idealnym kwadratem, musimy znaleźć pierwiastek kwadratowy z 196

idealny kwadrat 196

otwórz menu ustawień

Tutaj pierwiastek kwadratowy z 196 wynosi 14

Idealne kwadraty to liczby dodatnie, które można zapisać jako pomnożenie liczby przez nią samą lub można powiedzieć, że idealny kwadrat to liczba będąca potęgą 2 dowolnej liczby całkowitej.

Tutaj możemy napisać √196 = 14 lub 14²= 14 × 14 = 196.

Dlatego 196 jest idealnym kwadratem.

Podobne pytania

Pytanie 1: Jaki jest pierwiastek kwadratowy z 625?

Rozwiązanie:

idealny kwadrat 625

jak wyłączyć tryb programisty w Androidzie

tutaj 625 jest idealnym kwadratem 25

Możemy więc zapisać jako √625 = 25 lub 25²= 25 × 25 = 625

Pytanie 2: Jak znaleźć pierwiastek kwadratowy z 24?

Rozwiązanie:

pierwiastek kwadratowy z 24

Tutaj 24 nie jest idealnym kwadratem 4,8989..

Dlatego √24 = 4,8989..

Pytanie 3: Znajdź pierwiastek kwadratowy z 361?

Rozwiązanie:

kwadrat 361

Tutaj pierwiastek kwadratowy z 361 wynosi 19 , liczba całkowita będąca idealnym kwadratem

Dlatego √361 = 19 lub 19²= 19 × 19 = 361