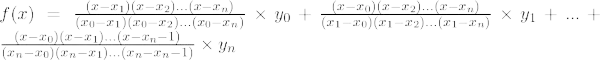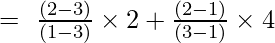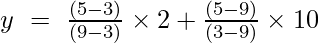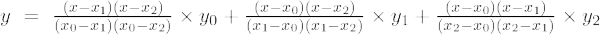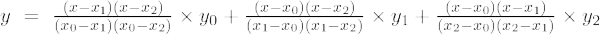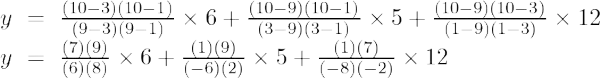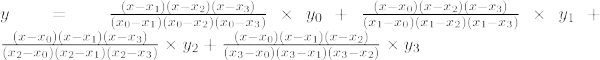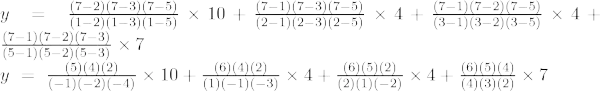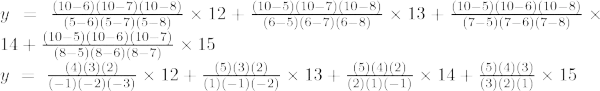logo

TechCodeview

Wzór interpolacji Lagrange'a

Wzór interpolacji Lagrange'a znajduje wielomian zwany wielomianem Lagrange’a, który przyjmuje określone wartości w dowolnym punkcie. Jest to n-ty stopień wyrażenie wielomianowe funkcji f(x). Metodę interpolacji stosuje się w celu znalezienia nowych punktów danych w zakresie dyskretnego zbioru znanych punktów danych.

pełna forma ssh

W tym artykule dowiemy się szczegółowo o interpolacji Lagrange'a, wzorze interpolacji Lagrange'a, dowodzie wzoru interpolacji Lagrange'a, przykładach opartych na wzorze interpolacji Lagrange'a i innych szczegółowo.



Co to jest interpolacja Lagrange'a?

Interpolacja Lagrange'a to sposób na znalezienie wartości dowolnej funkcji w dowolnym punkcie, gdy funkcja ta nie jest podana. Używamy innych punktów funkcji, aby uzyskać wartość funkcji w dowolnym wymaganym punkcie.

Załóżmy, że mamy funkcję y = f(x), w której podstawienie wartości x daje różne wartości y. I otrzymujemy dwa punkty (x1, I1) i (x2, I2) na krzywej, wówczas wartość y przy x = a(stała) jest obliczana przy użyciu wzoru interpolacji Lagrange'a.

Wzór interpolacji Lagrange'a

Biorąc pod uwagę kilka rzeczywistych wartości x1, X2, X3, …, XNi y1, I2, I3, …, INi powstanie wielomian P o rzeczywistych współczynnikach spełniających warunki P(xI) = iI, ∀ i = {1, 2, 3, …, n} i stopień wielomianu P musi być mniejszy niż liczba wartości rzeczywistych, tj. stopień (P)



Wzór interpolacji Lagrange'a dla n-tego rzędu

Wzór interpolacji Lagrange'a dla ntwielomian stopnia podano poniżej:

Wzór interpolacji Lagrange'a dla n t porządek jest,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Wzór interpolacji pierwszego rzędu Lagrange'a

Jeśli Stopień wielomianu wynosi 1, wówczas nazywa się go wielomianem pierwszego rzędu. Wzór interpolacji Lagrange'a dla 1ulwielomiany rzędu to,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Wzór interpolacji drugiego rzędu Lagrange'a

Jeśli stopień wielomianu wynosi 2, nazywa się go wielomianem drugiego rzędu. Wzór interpolacji Lagrange'a dla wielomianów drugiego rzędu to:

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Dowód twierdzenia Lagrange'a

Rozważmy wielomian n-tego stopnia danej postaci,

f(x) = A0(x – x1)(x – x2)(x – x3)…(x – xN) + A1(x – x1)(x – x2)(x – x3)…(x – xN) + … + A(n-1)(x – x1)(x – x2)(x – x3)…(x – xN)

Obserwacje zastępcze xIdostaćI

Wstaw x = x0wtedy otrzymamy A0

f(x0) = i0= A0(X0- X1)(X0- X2)(X0- X3)…(X0- XN)

A 0 = i 0 /(X 0 - X 1 )(X 0 - X 2 )(X 0 - X 3 )…(X 0 - X N )

Podstawiając x = x1dostajemy A1

f(x1) = i1= A1(X1- X0)(X1- X2)(X1- X3)…(X1- XN)

A 1 = i 1 /(X 1 - X 0 )(X 1 - X 2 )(X 1 - X 3 )…(X 1 - X N )

Podobnie, zastępując x = xNdostajemy AN

f(xN) = iN= AN(XN- X0)(XN- X1)(XN- X2)…(XN- Xn-1)

A N = i N /(X N - X 0 )(X N - X 1 )(X N - X 2 )…(X N - X n-1 )

Jeśli podstawimy wszystkie wartości AIw funkcji f(x) gdzie i = 1, 2, 3, …n otrzymujemy wzór interpolacji Lagrange’a jako:

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} razy y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} azy y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Właściwości wzoru interpolacyjnego Lagrange'a

Poniżej omówiono różne właściwości wzoru interpolacji Lagrange'a:

  • Formuła ta służy do znalezienia wartości funkcji w dowolnym punkcie, nawet jeśli sama funkcja nie jest podana.
  • Stosuje się go nawet wtedy, gdy podane punkty nie są równomiernie rozmieszczone.
  • Podaje wartość zmiennej zależnej dla dowolnej zmiennej niezależnej należącej do dowolnej funkcji i dlatego jest wykorzystywane w analizie numerycznej do znajdowania wartości funkcji itp.

Zastosowania wzoru interpolacji Lagrange'a

Poniżej omówiono różne zastosowania wzoru interpolacji Lagrange'a:

  • Służy do znalezienia wartości zmiennej zależnej przy dowolnej zmiennej niezależnej, nawet jeśli sama funkcja nie jest podana.
  • Używa się go do skalowania obrazu.
  • Jest stosowany w modelowaniu AI.
  • Służy do nauczania NLP itp.

Czytaj więcej,

  • Wzór interpolacyjny
  • Wzór interpolacji liniowej

Przykłady wykorzystania wzoru interpolacji Lagrange'a

Przyjrzyjmy się kilku przykładowym pytaniom dotyczącym wzoru interpolacji Lagrange'a.

Przykład 1: Znajdź wartość y przy x = 2 dla danego zbioru punktów (1, 2), (3, 4)

Rozwiązanie:

Dany,

  • (X0, I0) = (1, 2)
  • (X1, I1) = (3, 4)

Wzór interpolacji Lagrange'a pierwszego rzędu to:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Przy x = 2

I =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Wartość y przy x = 2 wynosi 3

Przykład 2: Znajdź wartość y przy x = 5 dla danego zbioru punktów (9, 2), (3, 10)

Rozwiązanie:

Dany,

  • (X0, I0) = (9, 2)
  • (X1, I1) = (3, 10)

Wzór interpolacji Lagrange'a pierwszego rzędu to:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Przy x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Wartość y przy x = 5 wynosi 7,33

Przykład 3: Znajdź wartość y przy x = 1 dla danego zbioru punktów (1, 6), (3, 4), (2, 5)

Rozwiązanie:

pokaż użytkownikom mysql

Dany,

  • (X0, I0) = (1, 6)
  • (X1, I1) = (3, 4)
  • (X2, I2) = (2, 5)

Wzór interpolacji Lagrange'a drugiego rzędu to:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Przy x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)} azy 5

y = (12/2) + 0 + 0

y = 6

Wartość y przy x = 1 wynosi 6

Przykład 4: Znajdź wartość y przy x = 10 dla danego zbioru punktów (9, 6), (3, 5), (1, 12)

Rozwiązanie:

Dany,

  • (X0, I0) = (9, 6)
  • (X1, I1) = (3, 5)
  • (X2, I2) = (1, 12)

Wzór interpolacji Lagrange'a drugiego rzędu to:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Przy x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} azy 12

alternatywa dla xamppa

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Wartość y przy x = 10 wynosi 9,375

Przykład 5: Znajdź wartość y przy x = 7 dla danego zbioru punktów (1, 10), (2, 4), (3, 4), (5, 7)

Rozwiązanie:

Dany,

  • (X0, I0) = (1, 10)
  • (X1, I1) = (2, 4)
  • (X2, I2) = (3, 4)
  • (X3, I3) = (5, 7)

Wzór interpolacji Lagrange'a trzeciego rzędu to:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} azy y_3

Przy x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7

y = -50 + 64 – 60 + 35

y = 99 – 110 = -jedenaście

Wartość y przy x = 7 wynosi -11

Przykład 6: Znajdź wartość y przy x = 10 dla danego zbioru punktów (5, 12), (6, 13), (7, 14), (8, 15)

Rozwiązanie:

Dany,

zamień ciąg w ciągu Java
  • (X0, I0) = (5, 12)
  • (X1, I1) = (6, 13)
  • (X2, I2) = (7, 14)
  • (X3, I3) = (8, 15)

Wzór interpolacji Lagrange'a trzeciego rzędu to:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} azy y_3

Przy x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15

y = -48 + 195 – 280 + 150

y = 17

Wartość y przy x = 10 wynosi 17

Przykład 7: Znajdź wartość y przy x = 0 dla danego zbioru punktów (-2, 5), (1, 7)

Rozwiązanie:

Dany,

  • (X0, I0) = (-2, 5)
  • (X1, I1) = (1, 7)

Wzór interpolacji Lagrange'a pierwszego rzędu to:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Przy x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Wartość y przy x = 0 wynosi 6,33

Często zadawane pytania dotyczące wzoru interpolacji Lagrange'a

1. Co to jest wzór interpolacji Lagrange'a?

Wzór interpolacji Lagrange'a to wzór używany do znalezienia wartości zmiennej zależnej funkcji dla dowolnej zmiennej niezależnej, nawet jeśli sama funkcja nie jest podana.

2. Jakie są zastosowania wzoru interpolacji Lagrange'a?

Wzór Lagrangesa ma różne zastosowania we współczesnej matematyce i naukach o danych,

  • Służy do trenowania modelu AI.
  • Jest stosowany w przetwarzaniu obrazu.
  • Jest używany w wykresach 3-D i wyższych krzywych itp.

3. Co to jest wzór interpolacji Lagrange'a pierwszego rzędu?

Wzór interpolacji Lagrange’a pierwszego rzędu to:

f(x) = (x – x 1 )/(X 0 - X 1 )×f 0 + (x – x 0 )/(X 1 - X 0 )×f 1

4. Co to jest wzór interpolacji Lagrange'a drugiego rzędu?

Wzór interpolacji Lagrange’a drugiego rzędu to:

f(x) = [(x – x 1 )(x – x 2 )/(X 0 - X 1 )(X 0 - X 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(X 1 - X 0 )(X 1 - X 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(X 2 - X 0 )(X 2 - X 2 )]×f 0